In Ostwald and Walker's appratus, dry air is passed through a solution containing 20 gram of an organic non-volatile solute in 250 ml of water. Then the air was passed through pure water and then through a U-tube containing anhydroous CaCl2. The mass lost in solution is 26 gram and the mass gained in the U-tube is 26.48 gram. Calculate the molecular mass of organic solute.
To calculate the molecular mass of the organic solute using Ostwald and Walker's apparatus, we can follow these steps:
Step 1: Understand the Problem
We have a solution containing 20 grams of a non-volatile organic solute in 250 mL of water. The air passed through the solution loses mass due to the vaporization of the solvent, and the U-tube gains mass due to the absorption of this vapor by anhydrous CaCl₂. The mass lost in the solution is 26 grams, and the mass gained in the U-tube is 26.48 grams.
Step 2: Calculate the Loss of Mass of the Solvent
The loss in mass of the solvent can be calculated as:
Loss in mass of solvent=Mass gained in U-tube−Mass lost in solution
Loss in mass of solvent=26.48g−26g=0.48g
Step 3: Set Up the Relationship
According to Raoult's law, the relationship between the loss in mass of the solvent and the mole fraction of the solute is given by:
Loss in mass of solventMass gained in U-tube=P0−PP0=Mole fraction of solute
Substituting the values we have:
0.48g26.48g=Mole fraction of solute
Step 4: Calculate the Mole Fraction of Solute
Calculating the mole fraction:
Mole fraction of solute=0.4826.48≈0.0181
Step 5: Calculate Moles of Solvent
The number of moles of solvent (water) can be calculated using its density (approximately 1 g/mL) and molar mass (18 g/mol):
Mass of water=250mL×1g/mL=250g
Moles of water=250g18g/mol≈13.89mol
Step 6: Set Up the Mole Fraction Equation
Using the mole fraction definition:
Mole fraction of solute=Moles of soluteMoles of solute+Moles of solvent
Assuming the moles of solute is negligible compared to the moles of solvent:
0.0181=nn+13.89
Where n is the moles of solute.
Step 7: Solve for Moles of Solute
Rearranging gives:
0.0181(n+13.89)=n
0.0181n+0.251=n
n−0.0181n=0.251
0.9819n=0.251
n≈0.2510.9819≈0.255mol
Step 8: Calculate the Molar Mass
Using the formula for molar mass:
Molar mass=mass of solutemoles of solute=20g0.255mol≈78.43g/mol
Final Answer
The molecular mass of the organic solute is approximately 79 g/mol.
---
We have a solution containing 20 grams of a non-volatile organic solute in 250 mL of water. The air passed through the solution loses mass due to the vaporization of the solvent, and the U-tube gains mass due to the absorption of this vapor by anhydrous CaCl₂. The mass lost in the solution is 26 grams, and the mass gained in the U-tube is 26.48 grams.
The loss in mass of the solvent can be calculated as:
Loss in mass of solvent=Mass gained in U-tube−Mass lost in solution
Loss in mass of solvent=26.48g−26g=0.48g
According to Raoult's law, the relationship between the loss in mass of the solvent and the mole fraction of the solute is given by:
Loss in mass of solventMass gained in U-tube=P0−PP0=Mole fraction of solute
Substituting the values we have:
0.48g26.48g=Mole fraction of solute
Calculating the mole fraction:
Mole fraction of solute=0.4826.48≈0.0181
The number of moles of solvent (water) can be calculated using its density (approximately 1 g/mL) and molar mass (18 g/mol):
Mass of water=250mL×1g/mL=250g
Moles of water=250g18g/mol≈13.89mol
Using the mole fraction definition:
Mole fraction of solute=Moles of soluteMoles of solute+Moles of solvent
Assuming the moles of solute is negligible compared to the moles of solvent:
0.0181=nn+13.89
Where n is the moles of solute.
Rearranging gives:
0.0181(n+13.89)=n
0.0181n+0.251=n
n−0.0181n=0.251
0.9819n=0.251
n≈0.2510.9819≈0.255mol
Using the formula for molar mass:
Molar mass=mass of solutemoles of solute=20g0.255mol≈78.43g/mol
The molecular mass of the organic solute is approximately 79 g/mol.
Topper's Solved these Questions
- SOLUTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SOLUTIONSEXERCISE - ASSIGMENT (SECTION-J) AAKASH CHALLENGERS QUESTIONS
10 Videos
- SOLUTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SOLUTIONSEXERCISE - ASSIGMENT (SECTION-G) TRUE-FALSE TYPE QUESTIONS
5 Videos
- REDOX REACTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - REDOX REACTIONSEXERCISE - ASSIGNMENT SECTION - D
10 Videos
- SOME BASIC CONCEPT OF CHEMISTRYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SOME BASIC CONCEPT OF CHEMISTRYEXERCISE - ASSIGNMENT( SECTION - D) Assertion-Reason Type Questions
15 Videos
Similar Questions
A current of dry air was bubbled through in a bulb containing 26.66g of a n organic substance in 200gms of water, then through a bulb at the same temperature containing pure water and finally through a tube containing fused calcium chloride. The loss in weight of water bulb is 0.0870 gms and gain in weight of CaCl2 tube is 2.036 gm. Calculate the molecular weight of the organic substance in the solution.
View SolutionDry air was passed successively through solution of 5g of a solute in 180g of water and then through pure water. The loss in weight of solution was 2.50g and that of pure solvent 0.04g. The molecualr weight of the solute is:
View SolutionLowering in vapour pressure is determined by Ostwald and Walker dynamic methed. It is based on the prinicipal , that when air is allowed to pass through a solvent or solution, it takes up solventvapour with it to get itself saturated at that temperature
I and II are weighted separately before and after passing dry air. Loss in mass of each set, gives the lowing of vapour pressure. The temperature of air, the solution and the solvent is kept constant.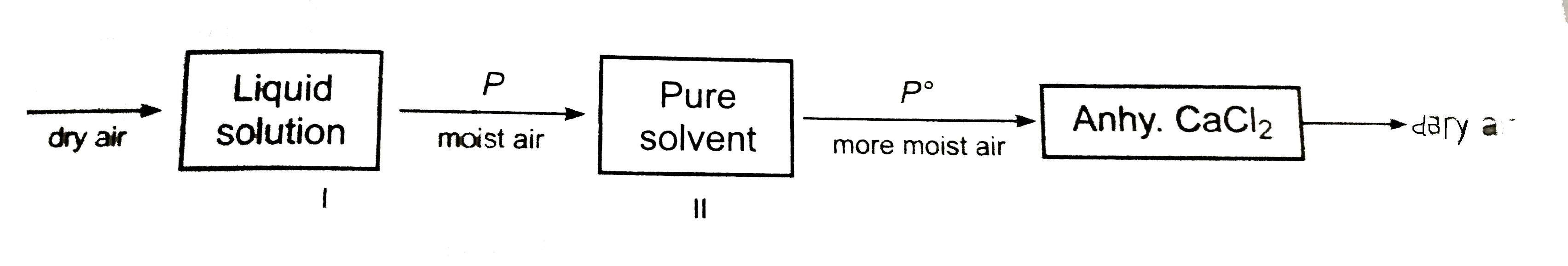
Dry air was passed thorough 9.24 g of solute in 108 g of water and then through pure water. The loss in mass of solution was 3.2 g and that of pure water 0.08 g . The molecular mass (g/mol) of solute is nearly :
(a)50
(b)62
(c)70
(d)80
View SolutionA solution containing 30g of a non-volatile solute in exactly 90g of water has a vapour pressure of 21.85mm of 25∘C . Further 18g of water is then added to the solution, the new vapour pressure becomes 22.15mm of Hg at 25C. Calculate the (a) molecular mass of the solute and (b) vapour pressure of water at 25∘C.
View SolutionA solution containing 8.6 g urea in one litre was found to be isotonic with 0.5% (mass/vol) solution of an organic, non volatile solute. The molecular mass of organic non volatile solute is:
View SolutionA solution containing 30 g of a non-volatile solute exactly in 90 g water has a vapour pressure of 2.8 k Pa at 298 K. Further 18 g of water is then added to solution, the new vapour pressure becomes 2.9 k Pa at 298 K. Calculate.
(i) Molecular mass of the solute
(ii) Vapour pressure of water at 298 K.
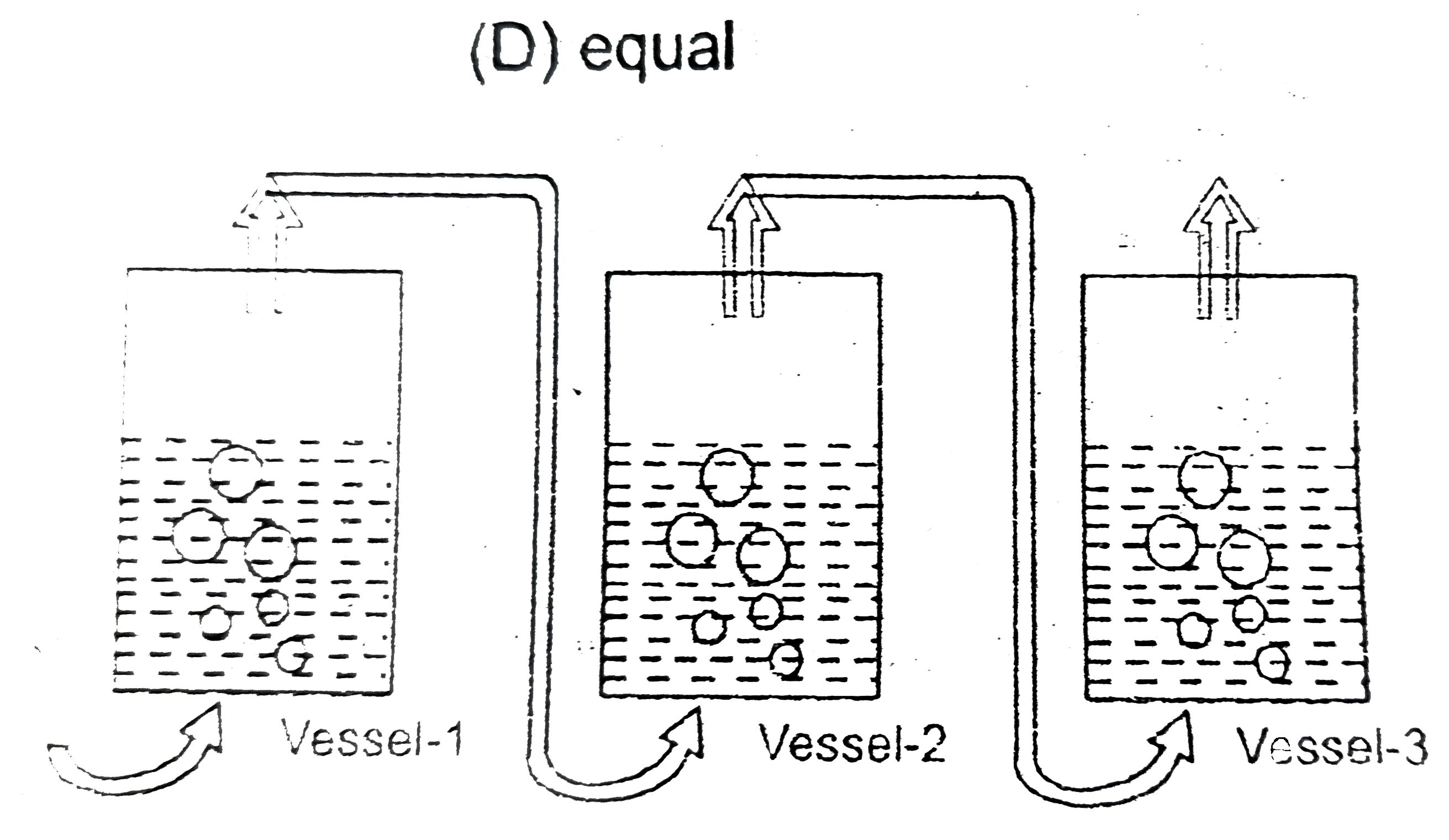
View SolutionDry air is slowly passed through three solutions of different concentrations, C1,C2 and C3, each containing (non-volatile) NaCl as solute and water as solvent, as shown in the Fig. If the vessel 2 gains weight and the vesel 3 loses weight then:
View SolutionA current of dry air was passed first through a series of bulbs containing a solution of C6H5−NO2 in ethanol of molality 0.725 and then through a series of bulbs containing pure ethanol. (T = 284 K) loss in weight of the solvent bulbs was 0.0685 g. Calculate the loss in weight of the solution bulbs.
View SolutionA solution contains non-volatile solute of molecular massM2which of the following can be used to calculate the molecular mass of solute in terms of osmotic pressure?
(m2 =mass of solute,V=volume of solution,π =osmotic pressure)
View SolutionV.P. of solute containing 6gm of non volatile solute in 180gm of water is 20Torr/mm of Hg. If 1 mole water is further added in to the V.P. increase by 0.02. Torr calculate V.P. of pure water & molecular of non volatile solute.
View Solution
