A current of dry air was passed first through a series of bulbs containing a solution of C6H5−NO2 in ethanol of molality 0.725 and then through a series of bulbs containing pure ethanol. (T = 284 K) loss in weight of the solvent bulbs was 0.0685 g. Calculate the loss in weight of the solution bulbs.
4.60 g
5.20 g
2.50 g
2.05 g
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Identify the given data
- Molality of the solution, m=0.725
- Loss in weight of the solvent bulbs, ΔWsolvent=0.0685g
- Molar mass of ethanol, M2=46g/mol
- Temperature, T=284K (not directly needed for calculations)
Step 2: Calculate the ratio of moles of solvent to moles of solute
Using the formula for molality:
m=n1n2⋅1000M2
Where:
- n1 = number of moles of solute (C₆H₅NO₂)
- n2 = number of moles of solvent (ethanol)
Rearranging gives:
n2n1=m⋅M21000
Substituting the values:
n2n1=0.725⋅461000=0.03335
Step 3: Apply Raoult's Law
According to Raoult's Law:
P0−PsPs=n2n1
Where:
- P0 = vapor pressure of pure solvent
- Ps = vapor pressure of the solution
This can be rearranged to express the loss in weight of the solution bulbs:
P0−Ps=Ps⋅n2n1
Given that the loss in weight of the solvent bulbs corresponds to P0−Ps:
0.0685=Ps⋅0.03335
Step 4: Solve for Ps
Rearranging the equation gives:
Ps=0.06850.03335≈2.05g
Conclusion
The loss in weight of the solution bulbs is approximately 2.05 g.
---
- Molality of the solution, m=0.725
- Loss in weight of the solvent bulbs, ΔWsolvent=0.0685g
- Molar mass of ethanol, M2=46g/mol
- Temperature, T=284K (not directly needed for calculations)
Using the formula for molality:
m=n1n2⋅1000M2
Where:
- n1 = number of moles of solute (C₆H₅NO₂)
- n2 = number of moles of solvent (ethanol)
n2n1=m⋅M21000
Substituting the values:
n2n1=0.725⋅461000=0.03335
According to Raoult's Law:
P0−PsPs=n2n1
Where:
- P0 = vapor pressure of pure solvent
- Ps = vapor pressure of the solution
P0−Ps=Ps⋅n2n1
Given that the loss in weight of the solvent bulbs corresponds to P0−Ps:
0.0685=Ps⋅0.03335
Rearranging the equation gives:
Ps=0.06850.03335≈2.05g
The loss in weight of the solution bulbs is approximately 2.05 g.
Similar Questions
A current of dry air was bubbled through in a bulb containing 26.66g of a n organic substance in 200gms of water, then through a bulb at the same temperature containing pure water and finally through a tube containing fused calcium chloride. The loss in weight of water bulb is 0.0870 gms and gain in weight of CaCl2 tube is 2.036 gm. Calculate the molecular weight of the organic substance in the solution.
View SolutionDry air was passed successively through solution of 5g of a solute in 180g of water and then through pure water. The loss in weight of solution was 2.50g and that of pure solvent 0.04g. The molecualr weight of the solute is:
View SolutionThe same current if passed through solution of silver nitrate and cupric salt connected in series. If the weights of silver deposited is 1.08g. Calculate the weight of copper deposited
View SolutionIn Ostwald and Walker's appratus, dry air is passed through a solution containing 20 gram of an organic non-volatile solute in 250 ml of water. Then the air was passed through pure water and then through a U-tube containing anhydroous CaCl2. The mass lost in solution is 26 gram and the mass gained in the U-tube is 26.48 gram. Calculate the molecular mass of organic solute.
View Solution7g of a solute are dissolved in 200 g of a solvent (mol. Wt. 78) to prepare a solution. At a certain temperature dry air is sent into a solution and solvent continuously. The loss is weights of containers containing solutions and solvent are 0.975 g and 0.025 g. Calculate the molar mass of solute.
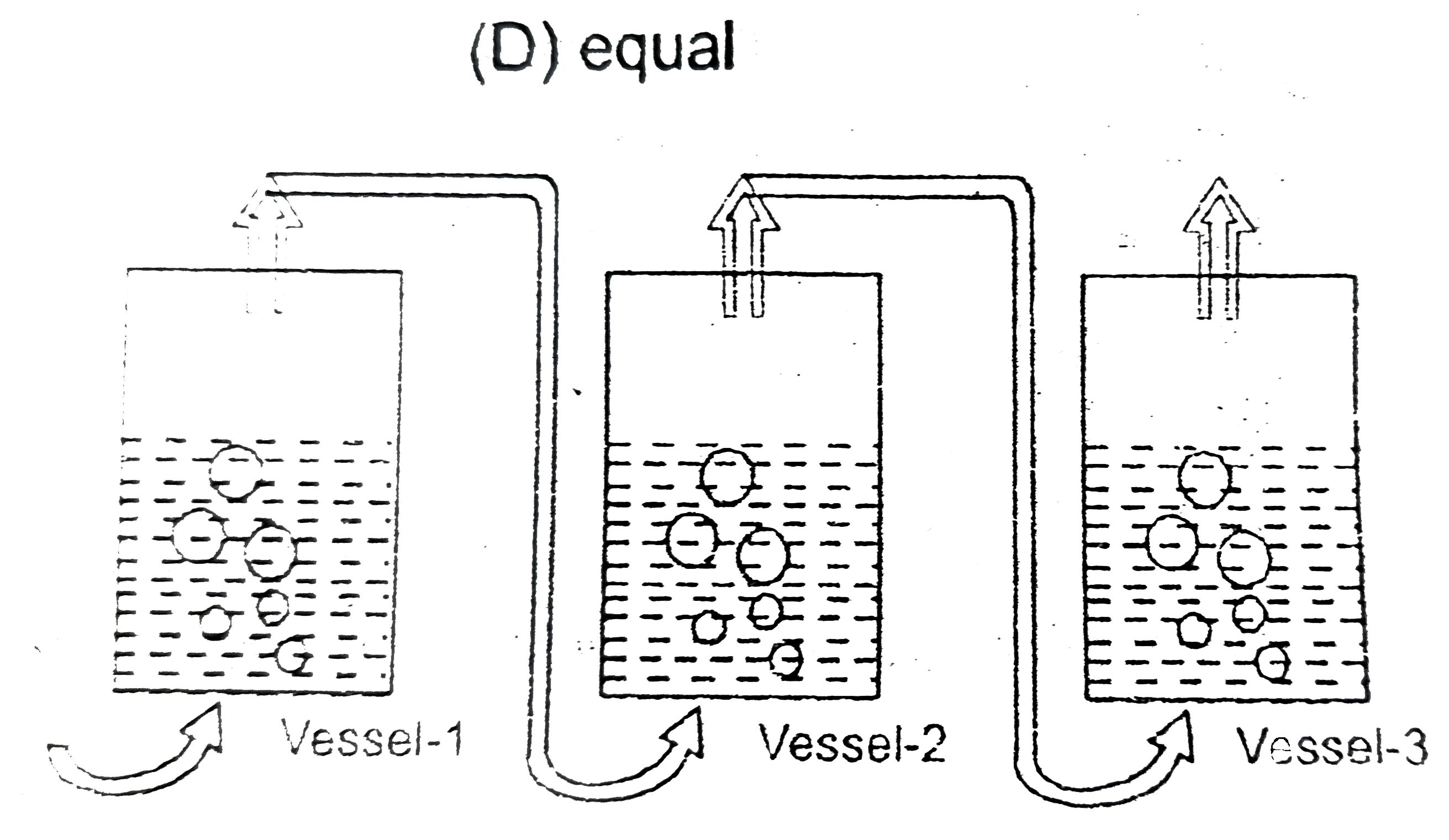
View SolutionDry air is slowly passed through three solutions of different concentrations, C1,C2 and C3, each containing (non-volatile) NaCl as solute and water as solvent, as shown in the Fig. If the vessel 2 gains weight and the vesel 3 loses weight then:
View SolutionA current strength of 1.0A is passed for 96.5s through 200mL of a solution of 0.05MKCl . Find
a. The amoudn of gases produced
b. The concentration of final solution w.r.t.c−OH ions
c.pH of the solution.
View SolutionIn an electrolysis experiment, current was passed for 5h through two cells connected in series. The first cell contains a solution of gold and second contains copper sulphate solution. In the first cell, 9.85g of gold was deposited. If the oxidation number of gold is +3, find the amount of copper deposited at the cathode of the second cell. Also calculate the magnitude of the current in ampere, ( Atomic weight of Au is 1197 and atomic weight of Cu is 63.5).
View SolutionA constant current was passed through a solution of AuClc−4 ion between gold electrodes. After a period of 10.0min, the increase in the weight of cathode was 1.314g. The total charge passed through solution is ( atomic weight of AuClc−4=339)
View Solution0⋅3605 g of a metal is deposited on the electrode by passing 1⋅2 amperes of current for 15 minutes through its salt solution. The atomic weight of the metal is 96. What is the valency of the metal ?
View Solution
