By how much will the potential of half-cell Cu2+∣Cu change if the solution is diluted to 100 times at 298K?
Increases by 59 mV
Decreases by 59 mV
Increases by 29.5 mV
Decreases by 29.5 mV
To determine how much the potential of the half-cell Cu2+∣Cu changes when the solution is diluted 100 times at 298 K, we can follow these steps:
Step 1: Understand the Nernst Equation
The Nernst equation relates the cell potential (E) to the standard potential (E°) and the concentrations of the reactants and products:
\( E = E^\circ - \frac{0.0591}{n} \log \left( \frac{(\text{products})}{(\text{reactants})} \right) \)
For the half-cell reaction:
\( \text{Cu}^{2+} + 2e^- \rightarrow \text{Cu (s)} \)
the Nernst equation becomes:
\( E = E^\circ - \frac{0.0591}{2} \log (\text{Cu}^{2+}) \)
Step 2: Initial Concentration
Let the initial concentration of \( \text{Cu}^{2+} \) be \( m \). Thus, the initial potential is:
\( E_{\text{initial}} = E^\circ - \frac{0.0591}{2} \log m \)
Step 3: Concentration After Dilution
When the solution is diluted 100 times, the new concentration of \( \text{Cu}^{2+} \) becomes:
\( (\text{Cu}^{2+})_{\text{new}} = \frac{m}{100} \)
Step 4: New Potential After Dilution
Substituting the new concentration into the Nernst equation gives:
\( E_{\text{new}} = E^\circ - \frac{0.0591}{2} \log \left( \frac{m}{100} \right) \)
Using the logarithmic property \( \log \left( \frac{a}{b} \right) = \log a - \log b \):
\( E_{\text{new}} = E^\circ - \frac{0.0591}{2} \left( \log m - \log 100 \right) \)
Since \( \log 100 = 2 \):
\( E_{\text{new}} = E^\circ - \frac{0.0591}{2} \left( \log m - 2 \right) \)
\( E_{\text{new}} = E^\circ - \frac{0.0591}{2} \log m + 0.0591 \)
Step 5: Change in Potential
Now, we can find the change in potential:
\( \Delta E = E_{\text{new}} - E_{\text{initial}} \)
\( \Delta E = \left( E^\circ - \frac{0.0591}{2} \log m + 0.0591 \right) - \left( E^\circ - \frac{0.0591}{2} \log m \right) \)
\( \Delta E = 0.0591 \)
Step 6: Convert to Millivolts
Since \( 0.0591 \) volts is equal to \( 59.1 \) millivolts, we conclude that:
The potential of the half-cell decreases by approximately 59.1 millivolts.
Final Answer
The potential of the half-cell Cu2+∣Cu will decrease by 59.1 millivolts when the solution is diluted to 100 times.
---
The Nernst equation relates the cell potential (E) to the standard potential (E°) and the concentrations of the reactants and products:
\( E = E^\circ - \frac{0.0591}{n} \log \left( \frac{(\text{products})}{(\text{reactants})} \right) \)
For the half-cell reaction:
\( \text{Cu}^{2+} + 2e^- \rightarrow \text{Cu (s)} \)
the Nernst equation becomes:
\( E = E^\circ - \frac{0.0591}{2} \log (\text{Cu}^{2+}) \)
Let the initial concentration of \( \text{Cu}^{2+} \) be \( m \). Thus, the initial potential is:
\( E_{\text{initial}} = E^\circ - \frac{0.0591}{2} \log m \)
When the solution is diluted 100 times, the new concentration of \( \text{Cu}^{2+} \) becomes:
\( (\text{Cu}^{2+})_{\text{new}} = \frac{m}{100} \)
Substituting the new concentration into the Nernst equation gives:
\( E_{\text{new}} = E^\circ - \frac{0.0591}{2} \log \left( \frac{m}{100} \right) \)
Using the logarithmic property \( \log \left( \frac{a}{b} \right) = \log a - \log b \):
\( E_{\text{new}} = E^\circ - \frac{0.0591}{2} \left( \log m - \log 100 \right) \)
Since \( \log 100 = 2 \):
\( E_{\text{new}} = E^\circ - \frac{0.0591}{2} \left( \log m - 2 \right) \)
\( E_{\text{new}} = E^\circ - \frac{0.0591}{2} \log m + 0.0591 \)
Now, we can find the change in potential:
\( \Delta E = E_{\text{new}} - E_{\text{initial}} \)
\( \Delta E = \left( E^\circ - \frac{0.0591}{2} \log m + 0.0591 \right) - \left( E^\circ - \frac{0.0591}{2} \log m \right) \)
\( \Delta E = 0.0591 \)
Since \( 0.0591 \) volts is equal to \( 59.1 \) millivolts, we conclude that:
The potential of the half-cell decreases by approximately 59.1 millivolts.
The potential of the half-cell Cu2+∣Cu will decrease by 59.1 millivolts when the solution is diluted to 100 times.
Topper's Solved these Questions
- ELECTROCHEMISTRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROCHEMISTRY EXERCISE - Assignment (SECTION C) Objective Type Questions (More than one option are correct)
16 Videos
- ELECTROCHEMISTRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROCHEMISTRY EXERCISE - Assignment (SECTION D) Linked Comprehension Type Questions
6 Videos
- ELECTROCHEMISTRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROCHEMISTRY EXERCISE - Assignment (SECTION A) Objective Type Questions (One option is correct)
43 Videos
- COORDINATION COMPOUNDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COORDINATION COMPOUNDS EXERCISE - Assignment (Section-J Aakash Challenger Questions )
10 Videos
- ENVIRONMENTAL CHEMISTRYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ENVIRONMENTAL CHEMISTRYEXERCISE - ASSIGNMENT (SECTION-D) (Assertion - Reason Type Questions)
4 Videos
Similar Questions
Knowledge Check
In the cell Zn∣∣Zn2+∣∣∣∣Cu2+∣∣Cu, the negaitve terminal is
ACuBCu2+CZnDZn2+The standard reduction potential for Cu2+/Cu is +0.34V. Calculate the reduction potential at pH=14 for the above couple. KSP of Cu(OH)2 is 1.0×10−19
A2.2 VB3.4 VC−0.22 VD−2.2 V
How much charge is required for the reduction of 1 mole of Cu2+ to Cu?
View SolutionState Faraday's first law of electrolysis . How much charge in terms of Faraday is required for the reduction of 1molofCu^(2+)→Cu.<br>(b)Calca––teemfofthefollow∈gcellat298 K : Mg(s) | Mg ^(2+)(0.1 M)||Cu^(2+) (0.01)|Cu(s)<br>[GivenE_(cell)^(@)=+ 2.71V, 1 F = 96500C mol^(-1)]
View SolutionThe enthalpy change ΔH for the neutralisation fo 1MHCI by caustic potash in dilute solution at 298K is
View SolutionThe standard reduction potential for Cu2+∣Cu is +0.34V. Calculate the reduction potential al pH=14 for the above couple . Ksp of Cu(OH)2 is 1.0×10−19
View SolutionThe reduction potential diagram for Cu in acid solution is :
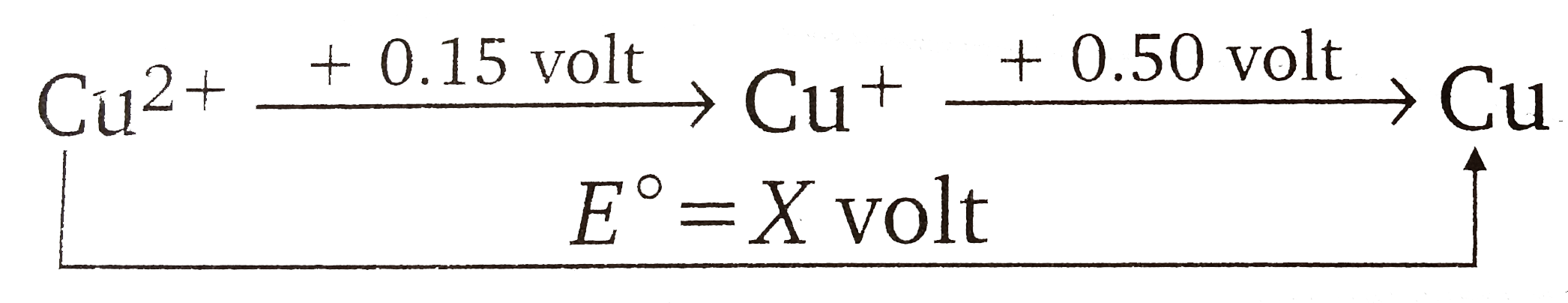
Calculate X. Does Cu+ disproportionate in solution ?
View SolutionThe EΘ values at 298 K corresponding to the following two reduction electrode processes are:
(i)Cu+/Cu=0.52V
(ii) Cu2+/Cu+=+0.16V
Formulate the galvanic cell for their combination. What will be the cell potential ? Calculate the ΔrGΘ for the cell reaction (F=96500 C mol−).
View Solution
