Graph between log x/m and log P is a straight line at angle of 45∘ with intercept 0.4771 on y-axis. Calculate the amount of gas adsorbed in gram per gram of adsorbent when pressure is 3 atm.
To solve the problem step by step, we will follow the information provided in the video transcript and apply the Langmuir adsorption isotherm.
1. Understanding the Graph:
The graph between log(x/m) and log(P) is a straight line at an angle of 45 degrees with an intercept of 0.4771 on the y-axis. This means that the slope (m) of the line is 1 (since tan(45°) = 1).
2. Langmuir Isotherm Equation:
The Langmuir adsorption isotherm can be expressed as:
log(xm)=log(k)+1nlog(P)
where:
- x = amount of gas adsorbed,
- m = mass of adsorbent,
- k = constant of adsorption,
- P = pressure of the gas,
- n = a positive integer.
3. Identifying the Intercept:
The y-intercept of the graph is given as 0.4771. This corresponds to log(k):
log(k)=0.4771
To find k, we can convert this logarithmic value back to its original form:
k=100.4771≈3
4. Finding the Value of n:
Since the slope of the line is 1, we have:
1n=1⟹n=1
5. Substituting Values into the Langmuir Equation:
Now, substituting k and n into the Langmuir equation:
log(xm)=log(3)+1⋅log(P)
Given that P=3atm:
log(P)=log(3)≈0.4771
6. Calculating log(x/m):
Now substituting the values into the equation:
log(xm)=log(3)+log(3)=0.4771+0.4771=0.9542
7. Finding x/m:
To find xm, we convert back from logarithmic form:
xm=100.9542≈8.99≈9
8. Conclusion:
The amount of gas adsorbed in grams per gram of adsorbent when the pressure is 3 atm is approximately 9 g/g.
The graph between log(x/m) and log(P) is a straight line at an angle of 45 degrees with an intercept of 0.4771 on the y-axis. This means that the slope (m) of the line is 1 (since tan(45°) = 1).
The Langmuir adsorption isotherm can be expressed as:
log(xm)=log(k)+1nlog(P)
where:
- x = amount of gas adsorbed,
- m = mass of adsorbent,
- k = constant of adsorption,
- P = pressure of the gas,
- n = a positive integer.
The y-intercept of the graph is given as 0.4771. This corresponds to log(k):
log(k)=0.4771
To find k, we can convert this logarithmic value back to its original form:
k=100.4771≈3
Since the slope of the line is 1, we have:
1n=1⟹n=1
Now, substituting k and n into the Langmuir equation:
log(xm)=log(3)+1⋅log(P)
Given that P=3atm:
log(P)=log(3)≈0.4771
Now substituting the values into the equation:
log(xm)=log(3)+log(3)=0.4771+0.4771=0.9542
To find xm, we convert back from logarithmic form:
xm=100.9542≈8.99≈9
The amount of gas adsorbed in grams per gram of adsorbent when the pressure is 3 atm is approximately 9 g/g.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SURFACE CHEMISTRY EXERCISE - TRY YOURSELF42videos
SURFACE CHEMISTRY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SURFACE CHEMISTRY EXERCISE - ASSIGNMENT SECTION - A51videos
SURFACE CHEMISTRY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRUCTURE OF ATOM EXERCISE - ASSIGNMENT ( SECTION -J) Aakash Challengers Questions12videos
STRUCTURE OF ATOM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXAMPLE134videos
TEST 1
Similar Questions
When a graph is plotted between log x/m and log p, it is straight line with an angle 45∘ and intercept 0.6020 on y-axis.if initial pressure is 0.3 atm, what will be the amount of gas adsorbed per gram of adsorbent :
View SolutionGraph between logx/m and logp is a straight line inclined at an angle of 45∘ . When pressure is 0.5atm and 1nk=0.693, the amount of solute adsorbed per gram of adsorbent will be:
View SolutionWhen a graph is plotted between log x/m and log p, it is straight line with an angle 45∘ and intercept 0.3010 on y− axis . If initial pressure is 0.3 atm, what wil be the amount of gas adsorbed per gm of adsorbent :
View SolutionGraph between log(xm) and logP is straight line at angle of 45∘ with the intercept of 0.6020.
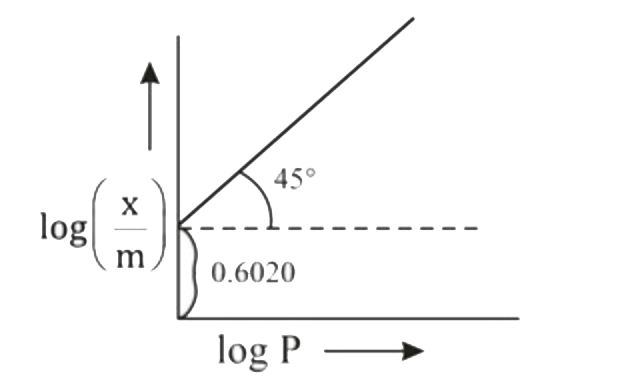
The extent of adsorption (xm) at a pressure of 1 atm isView SolutionIn an Adsorption experiment a graph between log x/m versus log P was found to be linear with a slope of 45∘ the intercept of the log x/m was found to be 0.3010. Calculate the amount of gas adsorbed per gram of charcoal under a pressure of 0.6 bar.
View SolutionIn an adsorption experiment, a graph between log (xm) versus log P was found to be linear with a slope of 45∘ . The intercept on the log y axis was found to be 0.301 . Calculate the amount of the gas adsorbed per gram of charcoal under a pressure of 3.0 atm.
View SolutionIn an adsorption experiment a graph between log xm versus log P was fond to be linear with a slope of 45∘). The intercept on the log xm axis was found to 0.70. Calculate the amount of gas adsorbed per gram of charcoal under a pressure of 1 atm [log5=0.70]
View SolutionPlot of log(x/m) against log P is a straight line inclined at an angle of 45∘. When the pressure is 0.5 atm and Freundlich parameter ,K is 10, the amount of solute adsorbed per gram of adsorbent will be : (log 5=0.6990 )
View SolutionIn an adsorption experiment, a graph between log (xm) versus log P was found to be linear with a slope of 45∘ . The intercept on the log (xm) axis was found to be 0.3010 . Calculate the amount of the gas adsorbed per gram of charcoal under a pressure of 0.5 atm .
View SolutionFor freundlich adsorption isotherm, a plot of log ( x/m) ( y - axis ) and log p (x-axis) gives a straight line . The intercept and slope for the line is 0.4771 and 2, respectively . The mass of gas , adsorbed per gram of adsorbent if the intital pressure is 0.04 atm , is ________ ×10−4 g.
(log 3=0.4771).View Solution

