In an adsorption experiment, a graph between log (xm) versus log P was found to be linear with a slope of 45∘ . The intercept on the log (xm) axis was found to be 0.3010 . Calculate the amount of the gas adsorbed per gram of charcoal under a pressure of 0.5 atm .
To solve the problem step by step, we will use the Freundlich adsorption isotherm and the information provided in the question.
Step 1: Understand the Freundlich Adsorption Isotherm
The Freundlich adsorption isotherm can be expressed as:
xm=kP1n
where:
- xm is the amount of gas adsorbed per gram of adsorbent (charcoal),
- k is a constant,
- P is the pressure,
- n is a constant related to the adsorption intensity.
Step 2: Take the Logarithm of Both Sides
Taking the logarithm of both sides, we get:
log(xm)=log(k)+1nlog(P)
Step 3: Identify the Linear Relationship
This equation can be rearranged to fit the linear equation y=mx+c:
- Let y=log(xm)
- Let x=log(P)
- The slope m=1n
- The intercept c=log(k)
Step 4: Use Given Values
From the problem:
- The slope is 45∘, which means tan(45∘)=1. Therefore, 1n=1 implies n=1.
- The intercept log(k)=0.3010.
Step 5: Calculate the Value of k
Since log(k)=0.3010:
k=100.3010=2
Step 6: Calculate xm at Given Pressure
Now we need to find xm when P=0.5 atm:
log(xm)=log(k)+1nlog(P)
Substituting the values:
log(xm)=0.3010+1⋅log(0.5)
Step 7: Calculate log(0.5)
We know:
log(0.5)=−0.3010
So substituting this in:
log(xm)=0.3010−0.3010=0
Step 8: Solve for xm
Now, we can find xm:
xm=100=1
Conclusion
The amount of gas adsorbed per gram of charcoal under a pressure of 0.5 atm is:
xm=1 gram of gas per gram of charcoal.
The Freundlich adsorption isotherm can be expressed as:
xm=kP1n
where:
- xm is the amount of gas adsorbed per gram of adsorbent (charcoal),
- k is a constant,
- P is the pressure,
- n is a constant related to the adsorption intensity.
Taking the logarithm of both sides, we get:
log(xm)=log(k)+1nlog(P)
This equation can be rearranged to fit the linear equation y=mx+c:
- Let y=log(xm)
- Let x=log(P)
- The slope m=1n
- The intercept c=log(k)
From the problem:
- The slope is 45∘, which means tan(45∘)=1. Therefore, 1n=1 implies n=1.
- The intercept log(k)=0.3010.
Since log(k)=0.3010:
k=100.3010=2
Now we need to find xm when P=0.5 atm:
log(xm)=log(k)+1nlog(P)
Substituting the values:
log(xm)=0.3010+1⋅log(0.5)
We know:
log(0.5)=−0.3010
So substituting this in:
log(xm)=0.3010−0.3010=0
Now, we can find xm:
xm=100=1
The amount of gas adsorbed per gram of charcoal under a pressure of 0.5 atm is:
xm=1 gram of gas per gram of charcoal.
Topper's Solved these Questions
- SURFACE CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Ex 5.1
11 Videos
- SURFACE CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Ex 5.2
11 Videos
- SURFACE CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Illustration 5.36
1 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
- SYNTHETIC AND NATURAL POLYMERSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SYNTHETIC AND NATURAL POLYMERSEXERCISE - Exercises Assertion Reasoning
10 Videos
Similar Questions
In an adsorption experiment, a graph between log (xm) versus log P was found to be linear with a slope of 45∘ . The intercept on the log y axis was found to be 0.301 . Calculate the amount of the gas adsorbed per gram of charcoal under a pressure of 3.0 atm.
View SolutionIn an adsorption experiment a graph between log xm versus log P was fond to be linear with a slope of 45∘). The intercept on the log xm axis was found to 0.70. Calculate the amount of gas adsorbed per gram of charcoal under a pressure of 1 atm [log5=0.70]
View SolutionIn an Adsorption experiment a graph between log x/m versus log P was found to be linear with a slope of 45∘ the intercept of the log x/m was found to be 0.3010. Calculate the amount of gas adsorbed per gram of charcoal under a pressure of 0.6 bar.
View SolutionIn an adsorption experiment, a graph of log(x/m) versus log P was found to be linear with a slope of 45°, and the the intercept is found to be 0.3010. The amount of gas adsorbed per gram charcoal under a pressure of 0.8 atm is
View SolutionWhen a graph is plotted between log x/m and log p, it is straight line with an angle 45∘ and intercept 0.3010 on y− axis . If initial pressure is 0.3 atm, what wil be the amount of gas adsorbed per gm of adsorbent :
View SolutionWhen a graph is plotted between log x/m and log p, it is straight line with an angle 45∘ and intercept 0.6020 on y-axis.if initial pressure is 0.3 atm, what will be the amount of gas adsorbed per gram of adsorbent :
View SolutionFor the adsorption of a gas on a solid, the plot of log(x/m) versus log P is linear with slope equal to:
View SolutionGraph between log x/m and log P is a straight line at angle of 45∘ with intercept 0.4771 on y-axis. Calculate the amount of gas adsorbed in gram per gram of adsorbent when pressure is 3 atm.
View SolutionFor the adsorption of a gas on a solid, the plot of log(x/m) versus log p is linear with slope equal to
View SolutionGraph between log(xm) and logP is straight line at angle of 45∘ with the intercept of 0.6020.
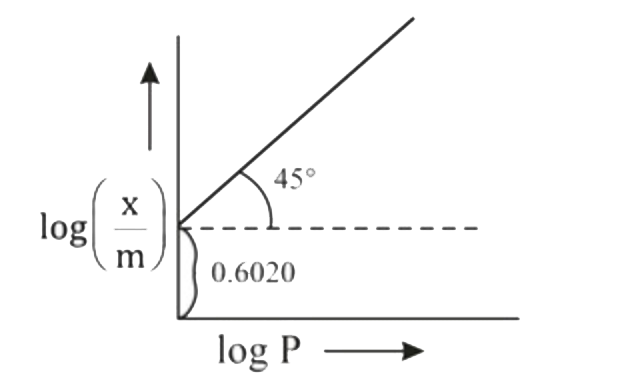
The extent of adsorption (xm) at a pressure of 1 atm is
View Solution
