A boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0.
Let the boat turns back at time and starts moving towards the raft. The separation between the raft and boat after a time interval t' measured from the moment of turning back is
The correct Answer is:1
To solve the problem, we need to analyze the motion of the boat and the raft step by step.
1. Understanding the Initial Setup:
- The boat can row in still water at a speed u.
- The river flows at a speed v.
- When the boat is moving downstream, its effective speed is u+v (boat speed + river speed).
- The raft moves with the river at speed v.
2. Distance Traveled by the Boat Before Turning Back:
- The boat overtakes the raft at t=0.
- Let the boat turn back at time t=t0.
- The distance traveled by the boat downstream in time t0 is given by:
Distanceboat=(u+v)t0
- This distance is the initial separation between the boat and the raft when the boat turns back.
3. Boat's Speed When Moving Upstream:
- After turning back, the boat moves upstream against the river's current.
- The effective speed of the boat when moving upstream is:
Speedupstream=u−v
4. Distance Traveled by the Boat and Raft After Turning Back:
- Let t′ be the time interval after the boat turns back.
- The distance traveled by the boat upstream during time t′ is:
Distanceboat=(u−v)t′
- The distance traveled by the raft downstream during the same time t′ is:
Distanceraft=vt′
5. Calculating the Separation After Time t′:
- The initial separation when the boat turns back is (u+v)t0.
- After time t′, the separation between the boat and the raft becomes:
Separation=Initial Separation−Distanceraft+Distanceboat
- Substituting the distances:
Separation=(u+v)t0−vt′+(u−v)t′
- Simplifying this expression:
Separation=(u+v)t0−vt′+ut′−vt′
=(u+v)t0−(v+v)t′+ut′
=(u+v)t0−2vt′+ut′
=(u+v)t0−ut′
6. Final Expression for Separation:
- The final expression for the separation between the raft and the boat after time t′ is:
Separation=ut0−ut′
Conclusion:
The correct answer is:
Separation=ut0−ut′
- The boat can row in still water at a speed u.
- The river flows at a speed v.
- When the boat is moving downstream, its effective speed is u+v (boat speed + river speed).
- The raft moves with the river at speed v.
- The boat overtakes the raft at t=0.
- Let the boat turn back at time t=t0.
- The distance traveled by the boat downstream in time t0 is given by:
Distanceboat=(u+v)t0
- This distance is the initial separation between the boat and the raft when the boat turns back.
- After turning back, the boat moves upstream against the river's current.
- The effective speed of the boat when moving upstream is:
Speedupstream=u−v
- Let t′ be the time interval after the boat turns back.
- The distance traveled by the boat upstream during time t′ is:
Distanceboat=(u−v)t′
- The distance traveled by the raft downstream during the same time t′ is:
Distanceraft=vt′
- The initial separation when the boat turns back is (u+v)t0.
- After time t′, the separation between the boat and the raft becomes:
Separation=Initial Separation−Distanceraft+Distanceboat
- Substituting the distances:
Separation=(u+v)t0−vt′+(u−v)t′
- Simplifying this expression:
Separation=(u+v)t0−vt′+ut′−vt′
=(u+v)t0−(v+v)t′+ut′
=(u+v)t0−2vt′+ut′
=(u+v)t0−ut′
- The final expression for the separation between the raft and the boat after time t′ is:
Separation=ut0−ut′
The correct answer is:
Separation=ut0−ut′
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Try Yourself40videos
MOTION IN STRAIGHT LINE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - A)50videos
MOTION IN STRAIGHT LINE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D16videos
MOVING CHARGE AND MAGNESIUM
Similar Questions
A boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0.
The distance between the boat and raft at a later instant of time t isView SolutionA boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0. Let the boat turns back at time t = t0 and starts moving towards the raft.
After how much time, measured from the moment of turning back the boat will cross the raft again ?
Option 1 t0
Option 2 ut0u+v
Option 3 vt0u+v
Option 4 (v+v)t0u−vView Solution
Knowledge Check
- Question 1 - Select One
A boat travels 16 km upstream in 4hr and 12 km downstream in 6 hr. What is the speed (in km/h) of boat in still water?
A1B2C3D4
When we jump out of a boat standing in water it moves
View SolutionA boat is being rowed in a river. Air is also blowing. Direction of velocity vectors of boat, water and air in ground frame are as shown in diagram.
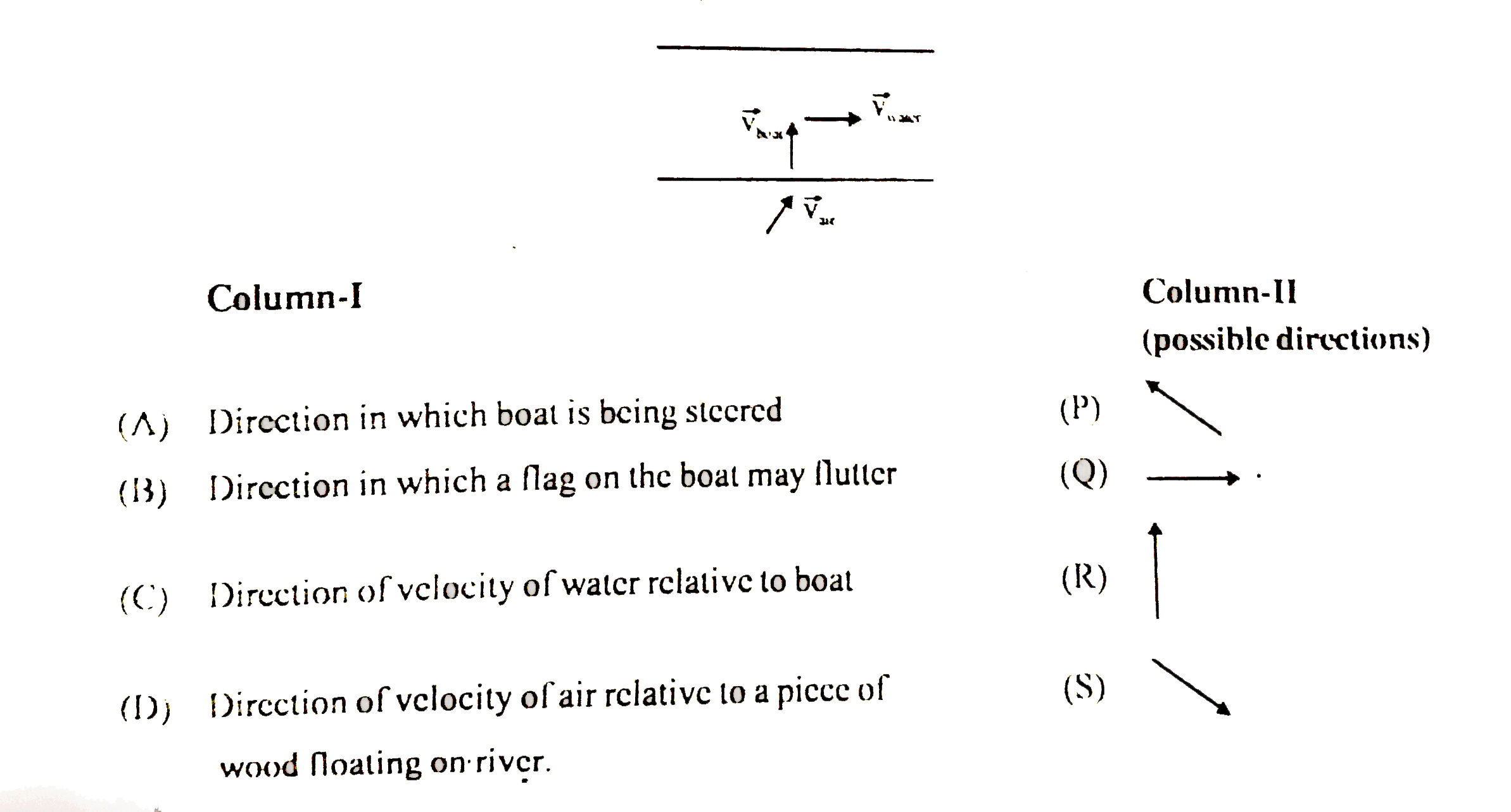 View Solution
View SolutionA boat goes 12 km upstream and 40 km downstream in 8 hours. It can go 16 km upstream and 32 km downstream in the same time. Find the speed of the boat in still water and the speed of the stream
View SolutionA boat, which can travel at a speed of 8 km/h in still water on a lake, is rowing in the flowing water in river. If the stream speed is 3 km/h, how fast the boat can cross a tree on the shore in traveling
upstream ?View SolutionA boat is moving with a velocity 3ˆi+4ˆj with respect to ground. The water in the river is moving with a velocity −3ˆi−4ˆj with respect to ground. The relative velocity of the boat with respect to water is.
View SolutionA boat is moving with a velocity vbw=5km/hr relative to water. At time t=0.the boat passes through a piece of cork floating in water while moving down stream.If it turns back at time t1=30min.
a) when the boat meet the cork again?
b) The distance travelled by the boat during this time.
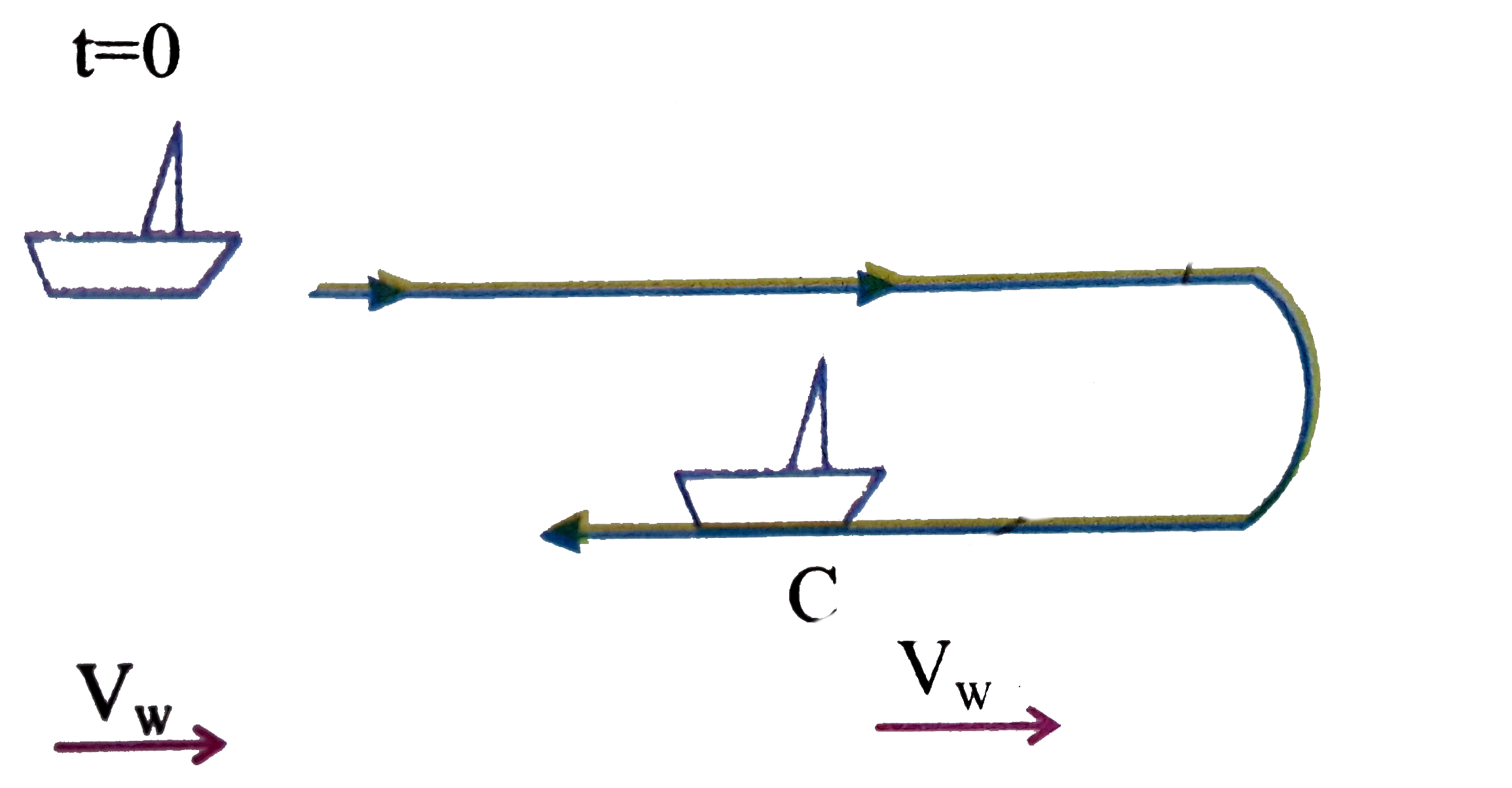 View Solution
View SolutionA man floating on a raft in water flowing at 2kmph observes a motor lauch overtaking him at t = 0. Then lauch travels with the speed of 20kmp relative to still water . After travelling for a time of 1 hr , the lauch turns back towards raft.How far from from the original point of crossing do they meet and what is the total time elapsed ?
View Solution

