A small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is $' μ'$ Using work-energy theorem, find the speed of block as it passes the lowest point.

Video Solution

Text Solution

Verified by Experts

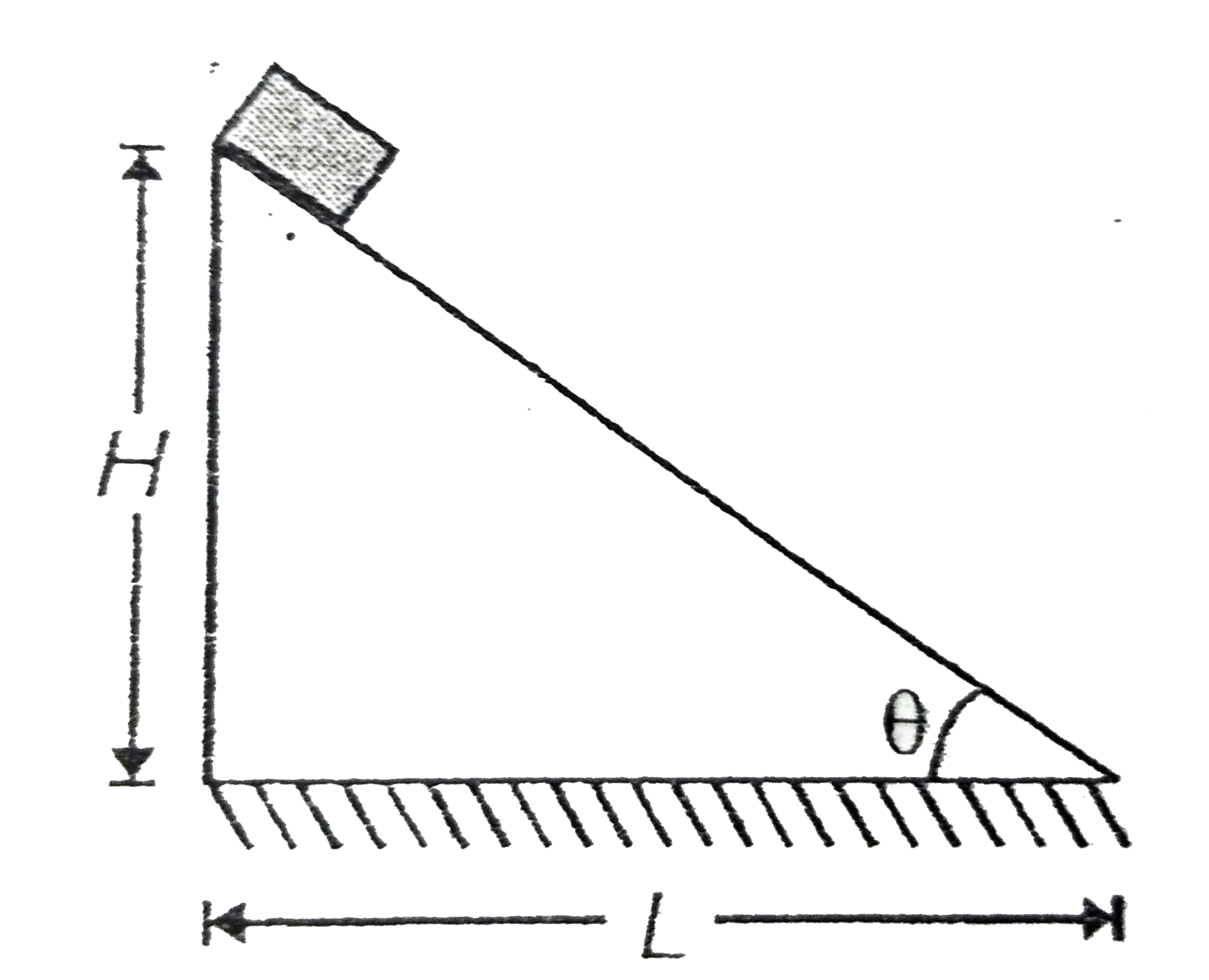
The FBD of the block is shown.

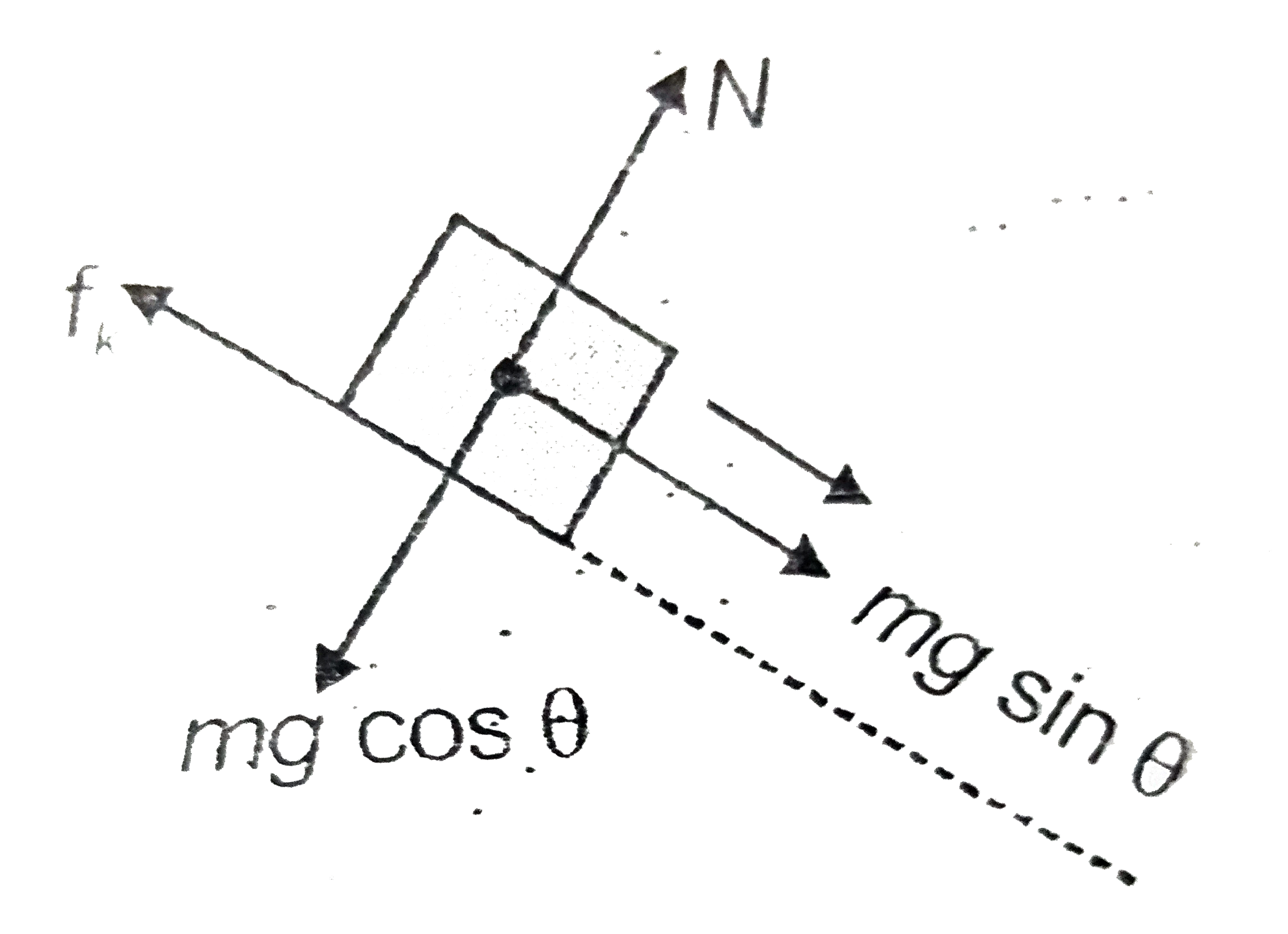
initial speed is zero final speed is v $\frac{1}{2} m v^{2} = 0 = W_{Total}$ We shall find the work done by each force
(1) $W_{N} = 0$
(2) $W_{m g cos θ} = 0$
(3) $W_{m g sin θ} = m g sin θ \times S \times {cos 0}^{\circ} = m g sin θ \times S - m g (\frac{H}{S}) \times S = m g H (∵ sin θ = \frac{H}{S})$
(4) $W_{f k} = μ N \times S \times {cos 180}^{\circ} = - μ m g cos θ \times S = - μ m g (\frac{L}{S}) \times S = - μ m g L (∵ cos θ = \frac{L}{S})$
$∴ W_{T o t a l} = m g H - μ m g L$
$∴ \frac{1}{2} m v^{2} = m g H - μ m g L or v = \sqrt{2 g (H - μ L)}$

Updated on:21/07/2023

|

Class 12 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

AAKASH INSTITUTE ENGLISH-WORK, ENERGY AND POWER-Assignment (SECTION - D)

Home
Ask Doubt
Profile