A block is released from rest from point on a rough inclined place of inclination 37∘. The coefficient of friction is 0.5.
The time taken to slide down 9 m on the plane is 3 s.
The velocity of block after moving 4 m is m/s.
The block travels equal distances in equal intervals of time.
The velocity of block increases linearly.
The correct Answer is:A, B, D
To solve the problem step by step, we will analyze the forces acting on the block on the inclined plane and then calculate the acceleration, time taken to slide down a certain distance, and the velocity after moving a specific distance.
Step 1: Identify the Forces Acting on the Block
1. Weight of the Block (W): The weight acts vertically downward and is given by W=mg.
2. Components of Weight:
- Parallel to the incline: W∥=mgsinθ
- Perpendicular to the incline: W_{\perpendicular} = mg \cos \theta
3. Normal Force (N): The normal force acts perpendicular to the incline and is equal to the perpendicular component of the weight: N=mgcosθ.
4. Frictional Force (F_f): The frictional force opposes the motion and is given by Ff=μN=μmgcosθ.
Step 2: Write the Equation of Motion
Since the block is sliding down the incline, we can write the equation of motion along the incline:
ma=mgsinθ−Ff
Substituting the expression for frictional force:
ma=mgsinθ−μmgcosθ
Dividing through by m:
a=gsinθ−μgcosθ
Step 3: Substitute Known Values
Given:
- θ=37∘
- μ=0.5
- g≈10m/s2
Calculate sin37∘ and cos37∘:
- sin37∘=35
- cos37∘=45
Now substitute these values into the equation for acceleration:
a=10(35)−0.5×10(45)
a=6−4=2m/s2
Step 4: Calculate Time to Slide Down 9 Meters
Using the equation of motion:
s=ut+12at2
Since the block is released from rest, u=0:
9=0+12×2×t2
9=t2
t=3s
Step 5: Calculate Velocity After Moving 4 Meters
Using the equation:
v2=u2+2as
Again, since u=0:
v2=0+2×2×4
v2=16⟹v=4m/s
Step 6: Analyze Distance Travelled in Equal Time Intervals
1. Distance in the first second (s1):
s1=12at2=12×2×12=1m
2. Distance in the first two seconds (s2):
s2=12at2=12×2×22=4m
3. Distance travelled in the second second (s2 - s1):
s2−s1=4−1=3m
The distances are not equal, therefore the statement is incorrect.
Step 7: Determine if Velocity Increases Linearly
Since the acceleration is constant (a=2m/s2), the velocity increases linearly with time.
Summary of Results
- Acceleration of the block: 2m/s2
- Time taken to slide down 9 meters: 3s
- Velocity after moving 4 meters: 4m/s
- The block does not travel equal distances in equal intervals of time.
- The velocity of the block increases linearly.
1. Weight of the Block (W): The weight acts vertically downward and is given by W=mg.
2. Components of Weight:
- Parallel to the incline: W∥=mgsinθ
- Perpendicular to the incline: W_{\perpendicular} = mg \cos \theta
3. Normal Force (N): The normal force acts perpendicular to the incline and is equal to the perpendicular component of the weight: N=mgcosθ.
4. Frictional Force (F_f): The frictional force opposes the motion and is given by Ff=μN=μmgcosθ.
Since the block is sliding down the incline, we can write the equation of motion along the incline:
ma=mgsinθ−Ff
Substituting the expression for frictional force:
ma=mgsinθ−μmgcosθ
Dividing through by m:
a=gsinθ−μgcosθ
Given:
- θ=37∘
- μ=0.5
- g≈10m/s2
- sin37∘=35
- cos37∘=45
a=10(35)−0.5×10(45)
a=6−4=2m/s2
Using the equation of motion:
s=ut+12at2
Since the block is released from rest, u=0:
9=0+12×2×t2
9=t2
t=3s
Using the equation:
v2=u2+2as
Again, since u=0:
v2=0+2×2×4
v2=16⟹v=4m/s
1. Distance in the first second (s1):
s1=12at2=12×2×12=1m
2. Distance in the first two seconds (s2):
s2=12at2=12×2×22=4m
3. Distance travelled in the second second (s2 - s1):
s2−s1=4−1=3m
The distances are not equal, therefore the statement is incorrect.
Since the acceleration is constant (a=2m/s2), the velocity increases linearly with time.
- Acceleration of the block: 2m/s2
- Time taken to slide down 9 meters: 3s
- Velocity after moving 4 meters: 4m/s
- The block does not travel equal distances in equal intervals of time.
- The velocity of the block increases linearly.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JM)
6 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (O-1)
51 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
Similar Questions
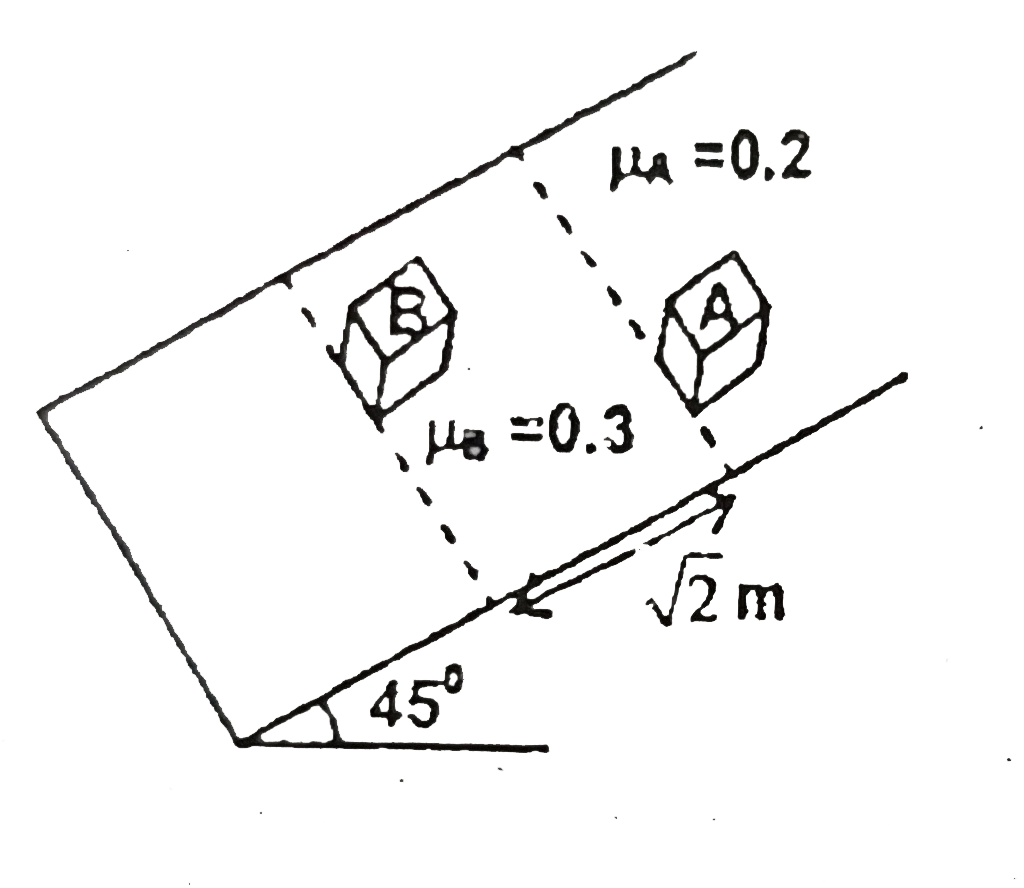
Two identical blocks A and B are placed on a rough inclined plane of inclination 45∘. The coefficient of friction between block A and incline is 0.2 and that of between B and incline is 0.3. The initial separation between the two blocks is √2m. The two blocks are released from rest, then find the time (in sec) after which front faces of both blocks come in same line.
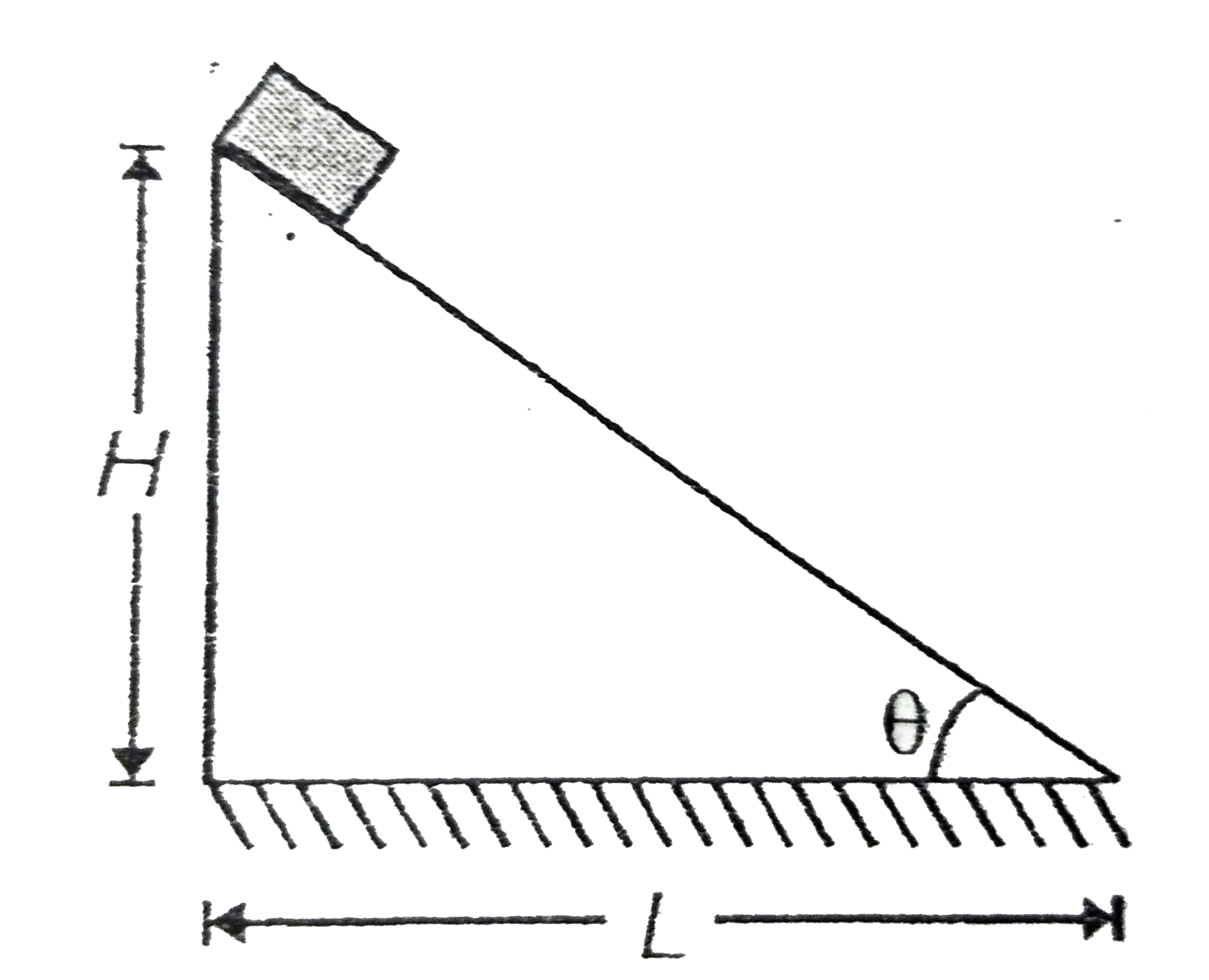
View SolutionA small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
View Solution
Knowledge Check
A block of mass m=2kg is resting on a rough inclined plane of inclination of 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)
 A2.68 NBZeroC4.34 ND6.24 N
A2.68 NBZeroC4.34 ND6.24 NA track has two inclined surface AB and DC each of length 3 m and angle of inclination of 30∘ with the horizontal and a central horizontal part of length 4m shown in figure. A block of mass 0.2 kg slides from rest from point A. The inclined surfaces are frictionless. If the coefficient of friction between the block and the horizontal flat surface is 0.2, where will the block finally come to rest ? [in 10−1m]
 A0.5 m away from point BB3.5 m away from point BC0.5 m away from point CD1.5 m away from point C
A0.5 m away from point BB3.5 m away from point BC0.5 m away from point CD1.5 m away from point C
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass 5 kg slides down a rough inclined surface. The angle of inclination is 45∘. The coefficient of sliding friction is 0.20. When the block slides 10 cm, the work done on the block by force of friction is
View SolutionA block of mass 10 kg is placed on rough inclined plane of inclination angle 37∘ .Coefficient of friction between block & plane is 0⋅8, find minimum magnitude of F so that block remains at rest .

View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View SolutionA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
View SolutionA block of mass 1 kg slides down a rough inclined plane of inclination 60∘ starting from its top. If coefficient of kinetic is 0.5 and length of the plane d=2 m, then work done against friction is
View Solution
