
Consider a uniform chain of mass m and length L, the chain is released when hanging length is L0. Find the speed with which the chain leaves the table.
(a) 
The part of the chain which is horizontal has zero potential energy as it is lying at the datum level. For the vertical part of chain, consider a small section of the chain at a distance x below the datum. The thickness of this section is dx and its mass is dm.
For this section, dU=−(dm)gx
Now, dm=mLdx
∴dU=−mgLxdx.
Integrating both sides, within proper limits,
U∫0dU=−mgLI∫0xdy⇒U=−mgl22L

As the end of chain just leaves the horizontal surface, chain becomes vertical. let its speed be v at this instant. So, its kinetic energy is 12mv2. The potential energy can be calculated as above, by taking limits of integration from zero to L.
U=−mgLL∫0xdx
⇒⇒U=−mgL2
As the table is smooth, there is no friction. Also workdone by normal reaction between chain and horizontal surface is zero. So machanical energy of the chain is conserved. We hav e
Ui+Ki=Uf+Kf
−mgl22L+0=−mgL2+12mv2
⇒v=√g(L−l2L)
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:IILUSTRATION
Explore 2 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:TRY YOURSELF
Explore 95 Videos
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
A uniform chain of mass 4 kg and length 2 m overhangs a smooth table with its one third part lying on the table Find the speed of chain as it completely slips of the table. (Take g=10ms2)
View SolutionA uniform chain of mass m and length l hanges on a thread and touches the surface of a table by its lower end. Find the force exerted by the table on the chain when half of its length has fallen on the table. The fallen part does not form heap.

View SolutionA chain of mass m and length l lies on a horizontal table. The chain is allowed to slide down gently from the side of the table. Find the speed of the chain at the instant when last link of the chain slides from the table. Neglect friction everywhere.
(a) the force from thelicopter and
(b) the gravitational force on her
(c ) What are speed ot the kinetic energy and.
(d) the speed of the astronaut just before she reaches the helicopter?
View SolutionA uniform chain of mass M and length L is hanging from the table. The chain is in limiting equilibrium when l length of chain over hangs . It is slightly disturbed from this position. Find the speed just after it completely comes off the table.
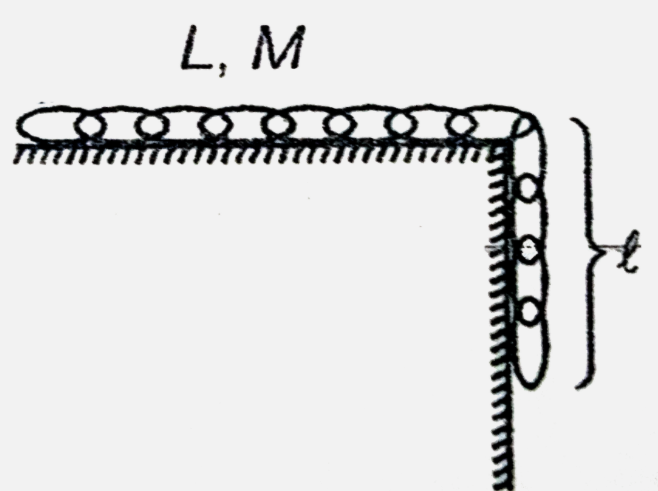
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

What is the speed of the chain, when it just loses contact with the table?
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

If the chain is limiting equlibrium, what is the coefficient of friction for the contact between table and chain?
View SolutionHalf length of the chain of mass m and length / is overhanging. What is speed of chain when it just slips off the smooth table?
View SolutionA uniform chain has a mass M and length L. It is placed on a frictionless table with length l0 hanging over the edge. The chain begins to slide down. Ten, the speed v with which the end slides down from the edge is given by
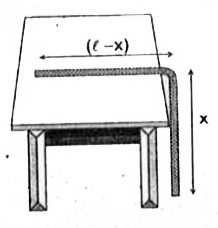
View SolutionA uniform chain of mass m and length I is kept on the table with a part of it overhanging (see figure). If the coefficient of friction between the table and the chain is 1/3 then find the maximum length of the chain that can overhang such that the chain remain in equilibrium.
View SolutionA uniform chain of mass m and length l is at the verge of sliding under the effect of gravity of the hanging part. Find the

a. coefficient of friction, between chain and table.
b. work done by friction and gravity till the chain leaves the table if the hanging part is pulled gently and released.
c. speed of the chain at the time of leaving the table in part (b) .
d. work done by the external force acting at the end A of the chain in slowly pulling the chain completely onto the table.
View Solution