Half length of the chain of mass m and length / is overhanging. What is speed of chain when it just slips off the smooth table?
√7gl
12√gl
12√5gl
12√3gl
To find the speed of the chain when it just slips off the smooth table, we can use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Understand the System
We have a chain of mass m and length L where half of the chain (length L2) is hanging off the table, and the other half is resting on the table.
Step 2: Identify Initial Potential Energy
Initially, the part of the chain that is hanging has potential energy. The center of mass of the hanging part (length L2) is located at a distance of L4 below the table. The potential energy (PE) of the hanging part is given by:
PEinitial=−(m2)g(L4)=−mgL8
Step 3: Identify Final Potential Energy
When the entire chain has slipped off the table, the center of mass of the entire chain (length L) is at a distance of L2 below the table. The potential energy of the entire chain is:
PEfinal=−mg(L2)=−mgL2
Step 4: Identify Kinetic Energy
When the chain slips off the table, it also has kinetic energy. The kinetic energy (KE) of the chain when it has just slipped off the table is given by:
KE=12mv2
Step 5: Apply Conservation of Energy
According to the conservation of energy, the initial potential energy plus the initial kinetic energy equals the final potential energy plus the final kinetic energy:
PEinitial+KEinitial=PEfinal+KEfinal
Substituting the values we have:
−mgL8+0=−mgL2+12mv2
Step 6: Simplify the Equation
Rearranging the equation gives:
12mv2=−mgL2+mgL8
To combine the terms on the right side, we convert −mgL2 to have a common denominator:
−mgL2=−4mgL8
Thus,
12mv2=−4mgL8+mgL8=−3mgL8
Step 7: Solve for Velocity
Now, multiplying through by 2 and dividing by m:
v2=3gL4
Taking the square root gives:
v=√3gL4=√3gL2
Final Result
Thus, the speed of the chain when it just slips off the smooth table is:
v=√3gL2
We have a chain of mass m and length L where half of the chain (length L2) is hanging off the table, and the other half is resting on the table.
Initially, the part of the chain that is hanging has potential energy. The center of mass of the hanging part (length L2) is located at a distance of L4 below the table. The potential energy (PE) of the hanging part is given by:
PEinitial=−(m2)g(L4)=−mgL8
When the entire chain has slipped off the table, the center of mass of the entire chain (length L) is at a distance of L2 below the table. The potential energy of the entire chain is:
PEfinal=−mg(L2)=−mgL2
When the chain slips off the table, it also has kinetic energy. The kinetic energy (KE) of the chain when it has just slipped off the table is given by:
KE=12mv2
According to the conservation of energy, the initial potential energy plus the initial kinetic energy equals the final potential energy plus the final kinetic energy:
PEinitial+KEinitial=PEfinal+KEfinal
Substituting the values we have:
−mgL8+0=−mgL2+12mv2
Rearranging the equation gives:
12mv2=−mgL2+mgL8
To combine the terms on the right side, we convert −mgL2 to have a common denominator:
−mgL2=−4mgL8
Thus,
12mv2=−4mgL8+mgL8=−3mgL8
Now, multiplying through by 2 and dividing by m:
v2=3gL4
Taking the square root gives:
v=√3gL4=√3gL2
Thus, the speed of the chain when it just slips off the smooth table is:
v=√3gL2
Topper's Solved these Questions
Similar Questions
A uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

What is the speed of the chain, when it just loses contact with the table?
View SolutionA man places a chain (of mass m and length l) on a table slowly. Initially, the lower end of the chain just touches the table. The main brings down the chain by length l/2. Work done by the man in this process is
View SolutionA chain of mass m and length l lies on a horizontal table. The chain is allowed to slide down gently from the side of the table. Find the speed of the chain at the instant when last link of the chain slides from the table. Neglect friction everywhere.
(a) the force from thelicopter and
(b) the gravitational force on her
(c ) What are speed ot the kinetic energy and.
(d) the speed of the astronaut just before she reaches the helicopter?
View SolutionA uniform chain of mass 4 kg and length 2 m overhangs a smooth table with its one third part lying on the table Find the speed of chain as it completely slips of the table. (Take g=10ms2)
View Solution
Consider a uniform chain of mass m and length L, the chain is released when hanging length is L0. Find the speed with which the chain leaves the table.
View SolutionA uniform flexible chain of mass m and length 2l hangs in equilibrium over a smooth horizontal pin of negligible diameter. One end of the chain is given a small vertical displacement so that the chain slips over the pin. The speed of chain when it leaves the pin is
View SolutionFind aC and α of the smooth rod of mass m and length l.
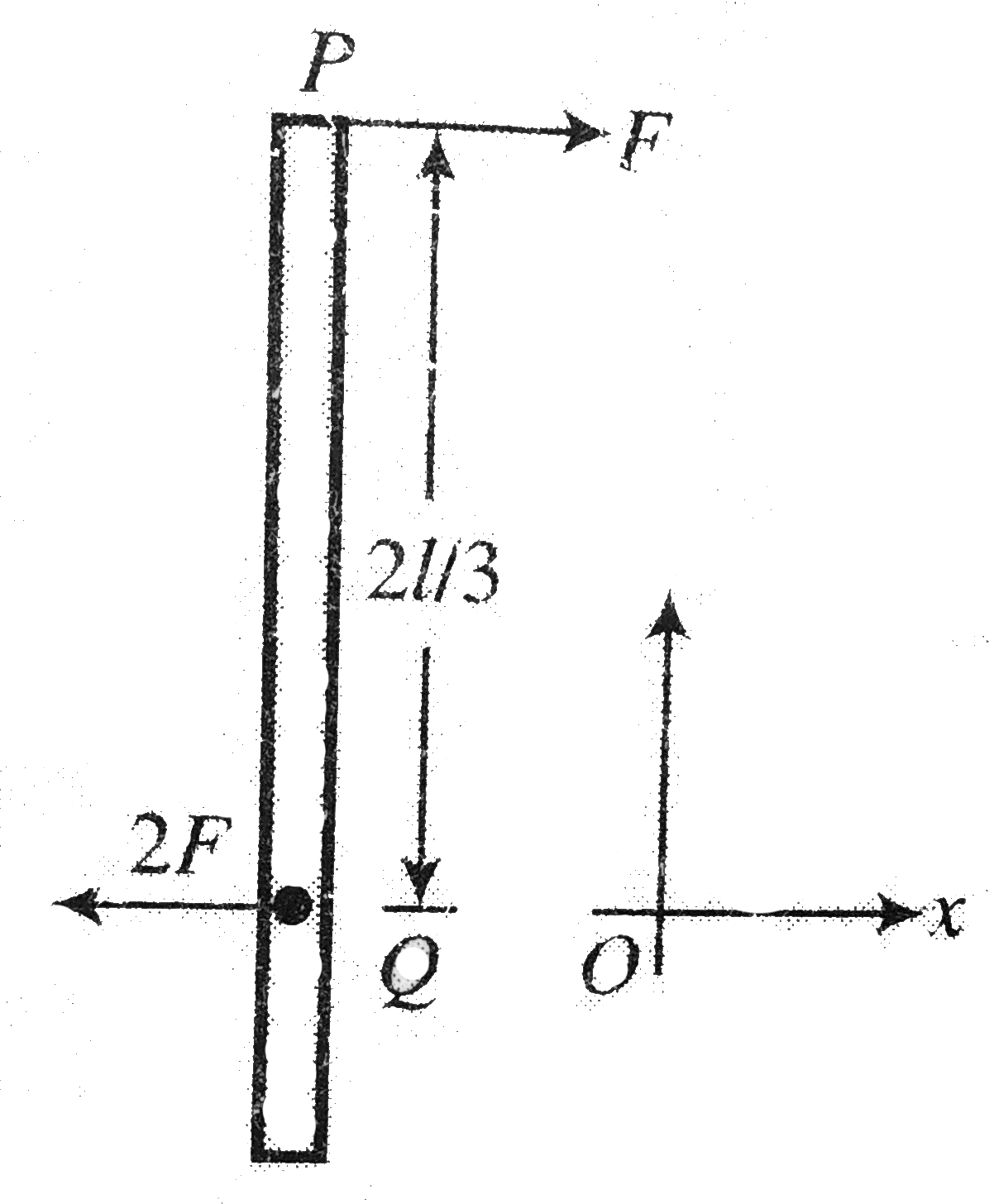
View SolutionA uniform flexible chain of mass m and length l hangs in equilibrium over a smooth horizontal pin of neglible diameter. One end of the chain is given a small verticle displacement so that the chain slips over the pin. The speed of chain when it leaves pin is
View SolutionA uniform chain of mass m and length l overhangs a table with its two third part on the table. Fine the work to be done by a person to put the hanging part back on the table.
View SolutionA very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
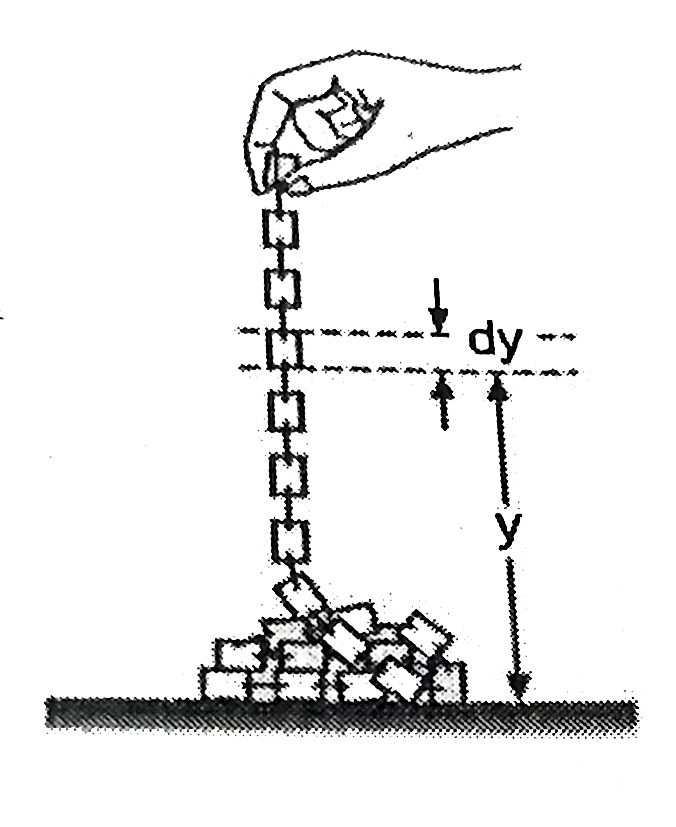
View Solution
