A car comes to a sliding stop in 5 m. During this process, the force on the car due to road is 100 N and is directed opposite to the motion.
(a) How much work done the road do on the car?
(b) How much work done the car do on the road?
To solve the problem step by step, we will analyze the situation involving the car, the forces acting on it, and the work done by these forces.
Step 1: Understand the Forces Acting on the Car
The car is coming to a stop due to the friction force exerted by the road. This friction force (F1) is given as 100 N and acts opposite to the direction of motion of the car.
Step 2: Identify the Displacement
The car slides to a stop over a distance of 5 meters. This is the displacement (d) we will use in our calculations.
Step 3: Calculate the Work Done by the Road on the Car
The work done (W) by a force is calculated using the formula:
W=F⋅d⋅cos(θ)
where:
- F is the force,
- d is the displacement,
- θ is the angle between the force and the displacement.
In this case:
- The force exerted by the road on the car (F1) is 100 N,
- The displacement (d) is 5 m,
- The angle (θ) between the force and the displacement is 180 degrees (since the force is opposite to the direction of displacement).
Substituting these values into the work formula:
W=100N×5m×cos(180∘)
Since cos(180∘)=−1:
W=100×5×(−1)=−500J
So, the work done by the road on the car is -500 Joules.
Step 4: Calculate the Work Done by the Car on the Road
Now, we will calculate the work done by the car on the road. The friction force exerted by the car on the road (F2) is also 100 N, but it acts in the same direction as the displacement of the car.
In this case:
- The force exerted by the car on the road (F2) is 100 N,
- The displacement (d) is still 5 m,
- The angle (θ) between the force and the displacement is 0 degrees (since the force and displacement are in the same direction).
Using the work formula again:
W=F⋅d⋅cos(θ)
Substituting the values:
W=100N×5m×cos(0∘)
Since cos(0∘)=1:
W=100×5×1=500J
So, the work done by the car on the road is 500 Joules.
Summary of Results
(a) The work done by the road on the car is -500 Joules.
(b) The work done by the car on the road is 500 Joules.
---
The car is coming to a stop due to the friction force exerted by the road. This friction force (F1) is given as 100 N and acts opposite to the direction of motion of the car.
The car slides to a stop over a distance of 5 meters. This is the displacement (d) we will use in our calculations.
The work done (W) by a force is calculated using the formula:
W=F⋅d⋅cos(θ)
where:
- F is the force,
- d is the displacement,
- θ is the angle between the force and the displacement.
- The force exerted by the road on the car (F1) is 100 N,
- The displacement (d) is 5 m,
- The angle (θ) between the force and the displacement is 180 degrees (since the force is opposite to the direction of displacement).
W=100N×5m×cos(180∘)
Since cos(180∘)=−1:
W=100×5×(−1)=−500J
Now, we will calculate the work done by the car on the road. The friction force exerted by the car on the road (F2) is also 100 N, but it acts in the same direction as the displacement of the car.
- The force exerted by the car on the road (F2) is 100 N,
- The displacement (d) is still 5 m,
- The angle (θ) between the force and the displacement is 0 degrees (since the force and displacement are in the same direction).
W=F⋅d⋅cos(θ)
Substituting the values:
W=100N×5m×cos(0∘)
Since cos(0∘)=1:
W=100×5×1=500J
(a) The work done by the road on the car is -500 Joules.
(b) The work done by the car on the road is 500 Joules.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-A (OBJECTIVE TYPE QUESTIONS (ONE OPTIONISCORRECT)60videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)45videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION2videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))12videos
WAVES
Similar Questions
A cyclist comes to a skidding stop in 10m. During this process, the force on the cycle due to the road is 200N and is directly opposite to the motion.
a. How much work does the road do on the cycle?
b. How much work does the cycle do on the road?View SolutionA cyclist comes to a skidding stop in 10m. During this process, the force on the cycle due to the road is 200N and is directly opposite to the motion.
a. How much work does the road do on the cycle?
b. How much work does the cycle do on the road?View Solution
Knowledge Check
- Question 1 - Select One
A bicyclist comes to a skidding stop in 10m. During this process, the force on the bicycle due to the road is 200N and is directly opposed to the motion. The work done by the cycle on the road is
A+2000 JB-200 JCzeroD-20000 J - Question 2 - Select One
How much work can be done by 100 calories of heat?
A100 JB420 JC42 JD4200 J
A bicyclist comes to a skidding stop in 10m. During this process, the force on the bicycle due to the road is 200N and is directly opposed to the motion. The work done by the cycle on the road is
View SolutionA bicyclist comes to a skidding stop in 10m. During this process, the force on the bicycle due to the road in 200N and is directly opposed to the motion. The work done by the cycle on the road is
View SolutionHow much work can be done by 100 calories of heat?
View SolutionA girl having mass of 35 kg sits on a trolley of mass 5 kg. The trolley is given an initial velocity of 4m//s by applying a force. The trolley comes to rest after travelling a distance of 16m. (a) How much work is done on the trolley ? (b) How much work is done by the girl ?
View SolutionA car travels with constant speed on a circular road level ground in figure Fair is the force of air resistence acts opposite to the motion of car which of the other forces shown best represents the horizontal force of the road on the car's tires?
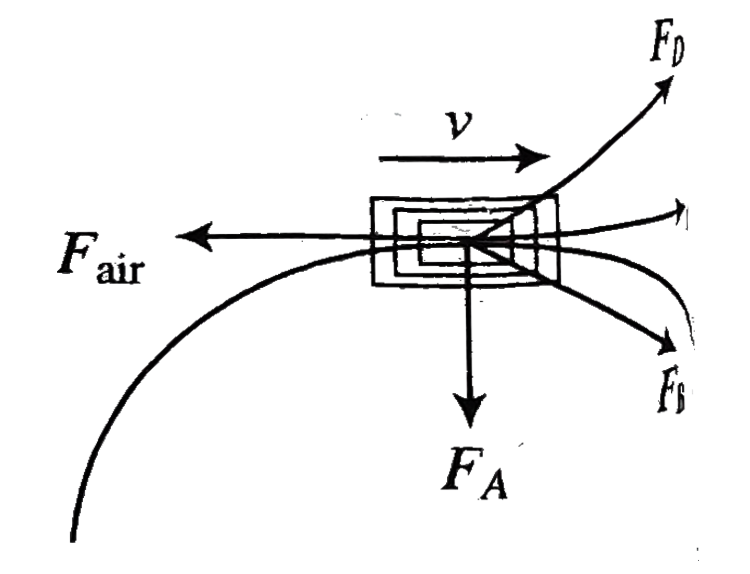 View Solution
View SolutionA car moves at a constant speed on a straigh but hilly road. One section has a crest and dip of the 250m radius.
(a) As the car passes over the crest the normal force on the car is half the 16kN weight of the car. What will the noraml force on the car its passes through th ebottom of the dip?
(b) What is the greatest speed at which the car can move without leaving the road at the top of the hill ?
(c) Moving at a speed found in part (b) what will be the normal force on the car as it moves through the bottom of the dip? (Take, g=10m/s2)View Solution

