Potential energy is defined
Only in conservative fields
As the negative work done by conservative forces
As the negative of work done by external forces when ΔK=0
All of these
The correct Answer is:A
To define potential energy, we can follow these steps:
Step 1: Understanding Potential Energy
Potential energy is the energy stored in an object due to its position in a force field, typically a gravitational or electric field. It is a form of mechanical energy.
Hint: Think about how energy can be stored based on an object's position relative to other objects or fields.
Step 2: Conservative Forces
Potential energy is associated with conservative forces. A conservative force is one where the work done by the force on an object moving between two points is independent of the path taken. The work done by a conservative force can be expressed in terms of potential energy.
Hint: Consider how the work done by a force relates to energy changes in a system.
Step 3: Mathematical Representation
The relationship between force (F) and potential energy (V) can be expressed mathematically as:
F=−dVdx
This equation indicates that the force is the negative gradient of the potential energy.
Hint: Remember that the negative sign indicates that the force acts in the direction of decreasing potential energy.
Step 4: Work Done by Conservative Forces
The work done by conservative forces can be defined as the negative change in potential energy:
W=−ΔV
This means that when work is done by conservative forces, potential energy decreases.
Hint: Think about how energy is transferred when work is done on or by an object.
Step 5: Non-Conservative Forces
In contrast, non-conservative forces (like friction) do not have a potential energy associated with them, and the work done depends on the path taken.
Hint: Consider examples of forces that do not conserve mechanical energy.
Conclusion
Based on the definitions and properties discussed, potential energy is specifically defined in the context of conservative fields. Therefore, the correct answer to the question is that potential energy is defined as existing only in conservative fields.
Final Answer: The correct option is A: only in conservative field.
Potential energy is the energy stored in an object due to its position in a force field, typically a gravitational or electric field. It is a form of mechanical energy.
Potential energy is associated with conservative forces. A conservative force is one where the work done by the force on an object moving between two points is independent of the path taken. The work done by a conservative force can be expressed in terms of potential energy.
The relationship between force (F) and potential energy (V) can be expressed mathematically as:
F=−dVdx
This equation indicates that the force is the negative gradient of the potential energy.
The work done by conservative forces can be defined as the negative change in potential energy:
W=−ΔV
This means that when work is done by conservative forces, potential energy decreases.
In contrast, non-conservative forces (like friction) do not have a potential energy associated with them, and the work done depends on the path taken.
Based on the definitions and properties discussed, potential energy is specifically defined in the context of conservative fields. Therefore, the correct answer to the question is that potential energy is defined as existing only in conservative fields.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)45videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS) (MORE THAN ONE OPTIONS ARE CORRECT)16videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF95videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))12videos
WAVES
Similar Questions
A block of mass 2 kg is kept at origin at t = 0 and is having velocity 4√5m/s in positive x - direction. The only force on it is a conservative and its potential energy is defined as U=−x3+6x2+15 (SI units). Its velocity when the force acting on it is minimum (after the time t = 0 ) is
View SolutionPotential energy is converted into kinetic energy by
View SolutionA: The value of potential energy depends on the reference taken for zero potential energy .
R : The value of change in potential energy is independent from reference level .View SolutionA body is executing simple harmonic motion. At a displacement x, its potential energy is E1 and a displacement y, its potential energy is E2. The potential energy E at a displacement (x+y) is
View SolutionA body is performing SHM At a displacement X1, its potential energy is 4 J and at a displacement X2, its potential energy is 9 J. The potential energy at a displacement (X1+X2) is
View SolutionWhich of the following statemente is / are INCORRECT?
(a) Mechanical energy is the sum of kinetic energy and potential energy.
(b) Potential energy is a relative quantity. It depends on the choice of reference point.
(c) Kinetic energy must be non negative.
(d) Potential energy must be postive.View SolutionA : The potential energy can be defined only in conservative field.
R : The value of potential energy depends on the reference level (level of zero potential energy).View SolutionDefine mechanical energy and law of conservation of mechanical energy. Prove conversion of gravitational potential energy in to kinetic energy by the help of law of conservation of mechanical energy. Also draw graph between energy and height.
View SolutionAssuming potential energy 'U' at ground level to be zero.
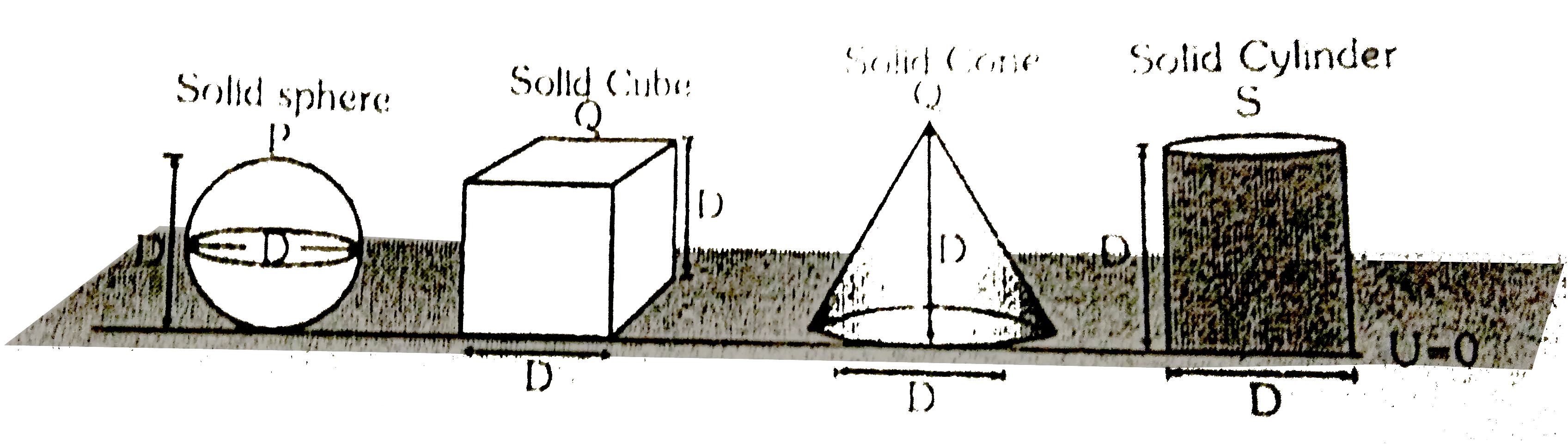
All objects are made up of same material :-
UP=Potential energy of solid sphereUQ=Potential energy of solid cubeUR=Potential energy of solid coneUS=Potential energy of solid cylinderView SolutionAssuming potential energy 'U' at ground level to be zero.

All objects are made up of same material :-
UP=Potential energy of solid sphereUQ=Potential energy of solid cubeUR=Potential energy of solid coneUS=Potential energy of solid cylinderView Solution

