A buttle weighting 10 g and moving with a velocity strikes a 10 kg block resting on a frictionless surface. The speed of the block after the perfectly inelastic collision is approximately
The correct Answer is:B
To solve the problem of a bullet colliding with a block in a perfectly inelastic collision, we can follow these steps:
Step 1: Identify the given values
- Mass of the bullet, m1=10g=10×10−3kg
- Velocity of the bullet, u1=800m/s
- Mass of the block, m2=10kg
- Initial velocity of the block, u2=0m/s
Step 2: Write the conservation of momentum equation
In a perfectly inelastic collision, the total momentum before the collision is equal to the total momentum after the collision. The equation is:
m1u1+m2u2=(m1+m2)V
Where V is the final velocity of the combined mass after the collision.
Step 3: Substitute the known values into the equation
Substituting the values we have:
(10×10−3kg)×(800m/s)+(10kg)×(0m/s)=(10×10−3kg+10kg)V
This simplifies to:
(10×10−3×800)=(10×10−3+10)V
Step 4: Calculate the left side of the equation
Calculating the left side:
10×10−3×800=8kg m/s
Step 5: Simplify the right side of the equation
The right side becomes:
(10×10−3+10)=10.01kg(approximately 10 kg)
Step 6: Set up the equation to solve for V
Now we can set up the equation:
8=10.01V
Step 7: Solve for V
To find V:
V=810.01≈0.8m/s
Step 8: Convert to centimeters per second
To convert V from meters per second to centimeters per second:
V=0.8m/s×100=80cm/s
Conclusion
The speed of the block after the perfectly inelastic collision is approximately 80cm/s.
- Mass of the bullet, m1=10g=10×10−3kg
- Velocity of the bullet, u1=800m/s
- Mass of the block, m2=10kg
- Initial velocity of the block, u2=0m/s
In a perfectly inelastic collision, the total momentum before the collision is equal to the total momentum after the collision. The equation is:
Substituting the values we have:
Calculating the left side:
The right side becomes:
Now we can set up the equation:
To find V:
To convert V from meters per second to centimeters per second:
The speed of the block after the perfectly inelastic collision is approximately 80cm/s.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)
Explore 45 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:SECTION-C (OBJECTIVE TYPE QUESTIONS) (MORE THAN ONE OPTIONS ARE CORRECT)
Explore 16 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:TRY YOURSELF
Explore 95 Videos
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
A bullet weighing 10 g and moving with a velocity 300 m/s strikes a 5 kg block of ice and drop dead. The ice block is kept on smooth surface. The speed of the block after the the collision is
View SolutionA steel ball of mass 0.5kg is fastened to a cord 20cm long and fixed at the far end and is released when the cord is horizontal. At the bottom of its path the ball strikes a 2.5kg steel block initially at rest on a frictionless surface. The collision is elastic. The speed of the block just after the collision will be.
View SolutionA 5 kg block rests on a horizontal surface. Which of the following option is incorrect? (g=10ms)

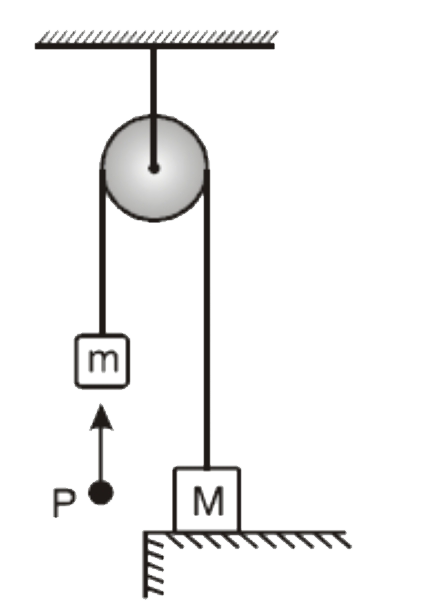
View SolutionA light inelastic thread passes over a small frictionless pulley. Two blocks of masses m = 1 kg and M = 3 kg, respectively, are attached with the thread and heavy block rests on a surface. A particle P of mass 1 kg moving upward with a velocity of 10ms−1 collides with the lighter block and sticks to it. The speed of the bigger block just after the string is taut will be [g=10ms−2]
View SolutionA bullet of mass 0.02 kg travelling horizontally with velocity 250ms−1 strikes a block of wood of mass 0.23 kg which rests on a rough horizontal surface. After the impact, the block and bullet move together and come to rest after travelling a distance of 40m. The coefficient of sliding friction of the rough surface is (g=9.8ms_2)
View SolutionAn object of mass 80 kg moving with velocity 2ms−1 hit by collides with another object of mass 20 kg moving with velocity 4ms−1 Find the loss of energy assuming a perfectly, inelastic collision
View SolutionAn object of mass 80 kg moving with velocity 2ms−1 hit by collides with another object of mass 20 kg moving with velocity 4ms−1 Find the loss of energy assuming a perfectly, inelastic collision
View SolutionA bullet of mass 50 g moving with an initial velocity 100m s−1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate : Retardation caused by the wooden block
View SolutionA bullet of mass 10g travelling horizontally with a velocity of 150ms−1 strikes a stationary wooden block and come to rest in 0.03s. Calculate the distance of penetration of the bullet into the block. Also, Calculate the magnitude of the force exerted by the wooden block on the bullet,
View SolutionA bullet of mass 10 g is fired horizontally into a 4 kg wooden block resting on a horizontal surface. The coefficient of kinetic friction between the block and the surface is 0.25. The bullet is embadded the block and the combination moves a distance of 20 m before coming to rest. Find the speed of the bullet just before striking the block. (g=10m/s2)
View Solution