A 5 kg body is fired vertically up with a speed of 200 m/s. Just before it hits the ground, its speed is 150 m/s. Over the entire trip,
Change in internal energy of the projectile and air is
The work done by gravity is 44000 J
The work done by gravity is zero
The time of upward motion is less than that for downward motion
The correct Answer is:A, C, D
To solve the problem, we will analyze the motion of the body fired vertically upward and then coming back down, taking into account the effects of gravity and air resistance.
1. Identify the Initial and Final Conditions:
- The mass of the body, m=5kg.
- Initial speed when fired upwards, u=200m/s.
- Final speed just before hitting the ground, v=150m/s.
2. Calculate the Change in Kinetic Energy:
- The initial kinetic energy (KE_initial) when the body is fired upwards can be calculated using the formula:
KEinitial=12mu2=12×5×(200)2=1000000J
- The final kinetic energy (KE_final) just before hitting the ground is:
KEfinal=12mv2=12×5×(150)2=562500J
3. Calculate the Change in Kinetic Energy:
- The change in kinetic energy (ΔKE) is given by:
ΔKE=KEfinal−KEinitial=562500−1000000=−437500J
- This negative value indicates that the body has lost kinetic energy during its trip.
4. Work Done by Air Resistance:
- The work done by air resistance (W_air) can be equated to the change in kinetic energy:
Wair=ΔKE=−437500J
- This means that air resistance has done negative work on the body, indicating energy loss.
5. Work Done by Gravity:
- Since the body returns to the same height from which it was fired, the total displacement is zero. Therefore, the work done by gravity (W_gravity) is:
Wgravity=0J
6. Conclusion about Internal Energy:
- The change in internal energy of the system (projectile and air) is not affected by the work done by gravity since it is zero. The loss in kinetic energy is due to air resistance, which means the internal energy change is also zero.
Final Answer:
- The work done by gravity is zero.
- The mass of the body, m=5kg.
- Initial speed when fired upwards, u=200m/s.
- Final speed just before hitting the ground, v=150m/s.
- The initial kinetic energy (KE_initial) when the body is fired upwards can be calculated using the formula:
KEinitial=12mu2=12×5×(200)2=1000000J
- The final kinetic energy (KE_final) just before hitting the ground is:
KEfinal=12mv2=12×5×(150)2=562500J
- The change in kinetic energy (ΔKE) is given by:
ΔKE=KEfinal−KEinitial=562500−1000000=−437500J
- This negative value indicates that the body has lost kinetic energy during its trip.
- The work done by air resistance (W_air) can be equated to the change in kinetic energy:
Wair=ΔKE=−437500J
- This means that air resistance has done negative work on the body, indicating energy loss.
- Since the body returns to the same height from which it was fired, the total displacement is zero. Therefore, the work done by gravity (W_gravity) is:
Wgravity=0J
- The change in internal energy of the system (projectile and air) is not affected by the work done by gravity since it is zero. The loss in kinetic energy is due to air resistance, which means the internal energy change is also zero.
- The work done by gravity is zero.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-D (LINKED COMPREHENSION TYPE QUESTIONS) (COMPREHENSION-I)
3 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-D (LINKED COMPREHENSION TYPE QUESTIONS) (COMPREHENSION-II)
3 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)
45 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A ball is projected vertically up with speed 20 m/s. Take g=10m/s2
View SolutionAt t=0, an arrow is fired vertically upwards with a speed of 100ms−1. A second arrow is fired vertically upwads with the same speed at t=5s. Then .
View SolutionA body is projected horizontally from the top of a tower with a velocity of 10m/s. If it hits the ground at an angle of 45∘, the vertical component of velocity when it hits ground in m/s is
View SolutionA ball is thrown upward with speed 10 m/s from the top to the tower reaches the ground with a speed 20 m/s. The height of the tower is [Take g=10m/s2]
View SolutionAn object is thrown vertically upward with a speed of 30 m/s. The velocity of the object half-a-second before it reaches the maximum height is
View SolutionA ball is thrown downwards with a speed of 20ms−1, from the top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30ms−1 from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
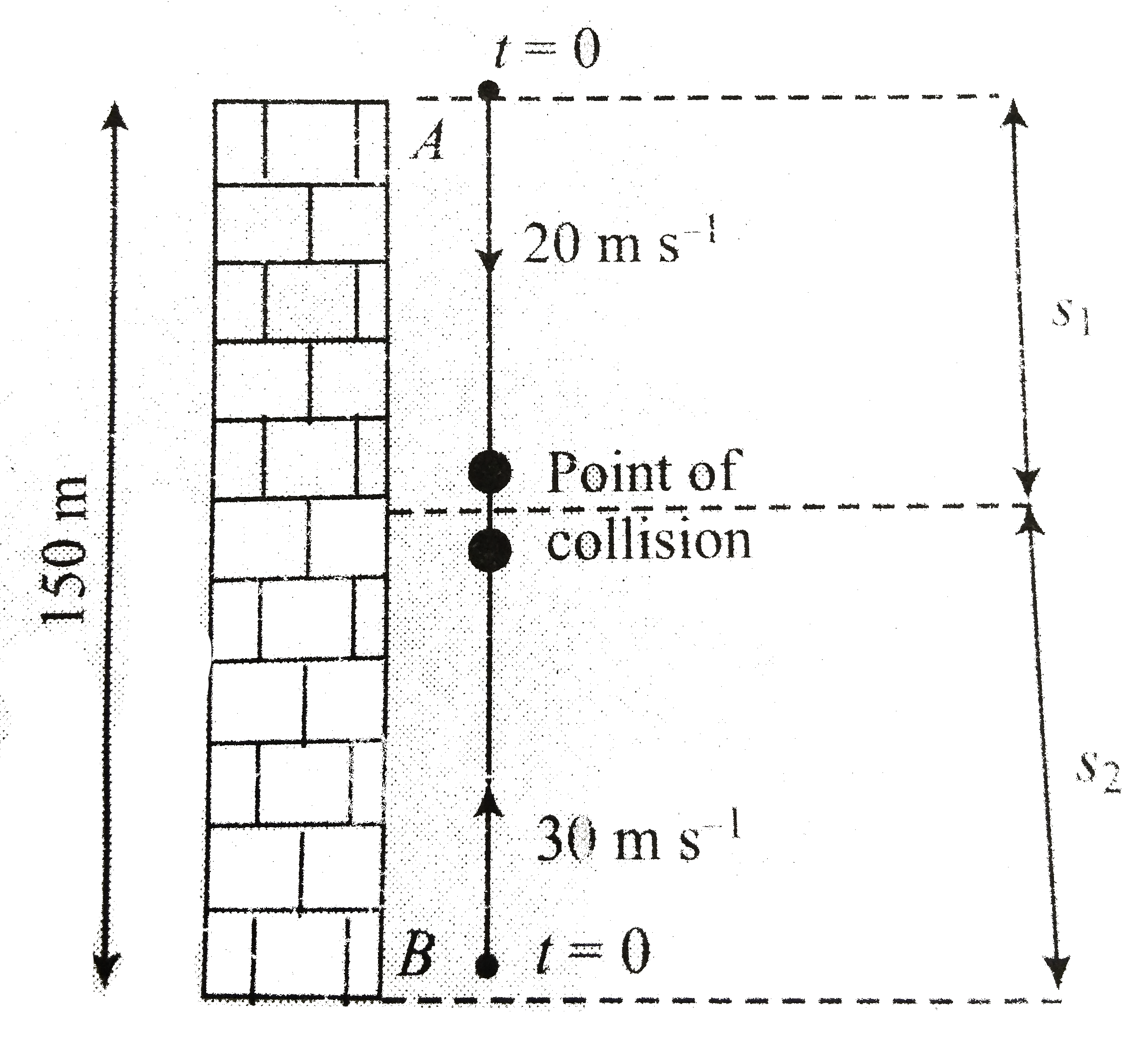 .
.
View SolutionA body is projected horizontally from the top of a tower with a velocity of 10m/s.If it hits the ground at an angle 45∘, then vertical component of velocity when it hits ground in m/s is
View SolutionAn aeroplane is flying vertically upwards. When it is at a height of 1000m above the ground and moving at a speed of 367m/s., a shot is fired at it with a speed of 567 ms−1 from a point directly below it. What should be the acceleration of aeroplane so that it may escape from being hit?
View SolutionA man standing on the edge of the terrace of a high rise building throws a stone, vertically up with at speed of 20m/s. Two seconds later, an identical stone is thrown vertically downwards with the same speed of 20m,. Then
View SolutionA stone is thrown vertically up at 20 m/s from a tower 80 m height. The speed with which it hits the ground is [g=10m/s2]
View Solution
