A light rigid rod of length l is hinged at one end and it is free to rotate in a vertical plane. A particle of mass m is attached to another end of the rod. The particle is released from rest at its highest point. Select the correct statement out of the following
Tension in the rod is zero when it makes an angle of cos−1(13) with the vertical
Tension in the rod is zero when it makes an angle of cos−1(23) with the vertical
Speed of partical of mass m is √23gl when the tension in the rod is zero
Speed of particle of mass m is √43gl when the tension in the rod is zero
The correct Answer is:B, C
To solve the problem step by step, we will analyze the motion of the particle attached to the rod when it is released from the highest point.
Step 1: Understand the Initial Setup
- A light rigid rod of length L is hinged at one end and free to rotate in a vertical plane.
- A particle of mass m is attached to the free end of the rod.
- The particle is released from rest at the highest point.
Hint: Visualize the setup and identify the forces acting on the mass when it is released.
Step 2: Determine Initial Potential Energy
- At the highest point, the height h of the mass m from the reference point (hinge) is equal to the length of the rod L.
- The initial potential energy PEinitial is given by:
PEinitial=mgh=mgL
Hint: Remember that potential energy is calculated using the formula PE=mgh.
Step 3: Determine Final Potential Energy
- As the rod rotates and the mass descends to an angle θ, the height of the mass from the hinge becomes Lcosθ.
- The final potential energy PEfinal is:
PEfinal=mg(Lcosθ)
Hint: The height changes as the mass moves, affecting the potential energy.
Step 4: Apply Conservation of Energy
- The change in potential energy will convert into kinetic energy. Thus, we can write:
PEinitial−PEfinal=KE
- The kinetic energy KE of the mass at angle θ is given by:
KE=12mv2
- Therefore, we have:
mgL−mgLcosθ=12mv2
Hint: Use the principle of conservation of energy to relate potential and kinetic energy.
Step 5: Simplify the Equation
- Cancel m from both sides:
gL(1−cosθ)=12v2
- Rearranging gives:
v2=2gL(1−cosθ)
Hint: Isolate v2 to find the relationship between speed and angle.
Step 6: Analyze Forces at Angle θ
- When the rod is at angle θ, the forces acting on the mass m are:
- Weight mg acting downward.
- Tension T in the rod acting along the rod.
- The centripetal force required for circular motion is provided by the tension and the component of weight along the rod:
T+mgcosθ=mv2L
Hint: Break down the forces acting on the mass into components.
Step 7: Find Condition for Zero Tension
- Set T=0 (the condition when tension is zero):
mgcosθ=mv2L
- Substitute v2 from the previous step:
mgcosθ=m(2gL(1−cosθ))L
- Simplifying gives:
mgcosθ=2mg(1−cosθ)
Hint: Setting tension to zero helps to find the angle at which this occurs.
Step 8: Solve for cosθ
- Cancel mg from both sides:
cosθ=2(1−cosθ)
- Rearranging gives:
3cosθ=2⇒cosθ=23
Hint: Rearranging the equation will help you isolate cosθ.
Step 9: Find the Angle θ
- To find θ, take the inverse cosine:
θ=cos−1(23)
Hint: Use a calculator or trigonometric tables to find the angle.
Step 10: Find the Speed of the Particle
- Substitute cosθ back into the equation for v2:
v2=2gL(1−23)=2gL(13)=2gL3
- Thus, the speed v is:
v=√2gL3
Hint: Make sure to simplify correctly to find the final expression for speed.
Final Results
- The angle at which tension is zero is θ=cos−1(23).
- The speed of the particle when the tension is zero is v=√2gL3.
- A light rigid rod of length L is hinged at one end and free to rotate in a vertical plane.
- A particle of mass m is attached to the free end of the rod.
- The particle is released from rest at the highest point.
- At the highest point, the height h of the mass m from the reference point (hinge) is equal to the length of the rod L.
- The initial potential energy PEinitial is given by:
PEinitial=mgh=mgL
- As the rod rotates and the mass descends to an angle θ, the height of the mass from the hinge becomes Lcosθ.
- The final potential energy PEfinal is:
PEfinal=mg(Lcosθ)
- The change in potential energy will convert into kinetic energy. Thus, we can write:
PEinitial−PEfinal=KE
- The kinetic energy KE of the mass at angle θ is given by:
KE=12mv2
- Therefore, we have:
mgL−mgLcosθ=12mv2
- Cancel m from both sides:
gL(1−cosθ)=12v2
- Rearranging gives:
v2=2gL(1−cosθ)
- When the rod is at angle θ, the forces acting on the mass m are:
- Weight mg acting downward.
- Tension T in the rod acting along the rod.
- The centripetal force required for circular motion is provided by the tension and the component of weight along the rod:
T+mgcosθ=mv2L
- Set T=0 (the condition when tension is zero):
mgcosθ=mv2L
- Substitute v2 from the previous step:
mgcosθ=m(2gL(1−cosθ))L
- Simplifying gives:
mgcosθ=2mg(1−cosθ)
- Cancel mg from both sides:
cosθ=2(1−cosθ)
- Rearranging gives:
3cosθ=2⇒cosθ=23
- To find θ, take the inverse cosine:
θ=cos−1(23)
- Substitute cosθ back into the equation for v2:
v2=2gL(1−23)=2gL(13)=2gL3
- Thus, the speed v is:
v=√2gL3
- The angle at which tension is zero is θ=cos−1(23).
- The speed of the particle when the tension is zero is v=√2gL3.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:SECTION-D (LINKED COMPREHENSION TYPE QUESTIONS) (COMPREHENSION-I)
Explore 3 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:SECTION-D (LINKED COMPREHENSION TYPE QUESTIONS) (COMPREHENSION-II)
Explore 3 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)
Explore 45 Videos
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
A uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is

View SolutionA conducting rod of length l is hinged at point O. It is a free to rotate in a verical plane. There exists a uniform magnetic field B in horizontal direction. The rod is released from the position shown. The potential difference between the two ends of the rod is proportional to

View SolutionAssertion One end of a massless rod of length l is hinged so that it is free to rotate in vertical plane about a horizontal axis. If a particle is attached to the other end of the rod, then the minimum speed at lower most position of the particle is √5gl to complete the circular motion.
Reason Work done by cnetripetal force on the particle is always zero.
View SolutionA light rigid rod of length 4m is connected rigidly with two identical particles each of mass m=2kg. the free end of the rod is smoothly pivoted at O. The rod is released from rest from its horizontal position at t=0. Find the
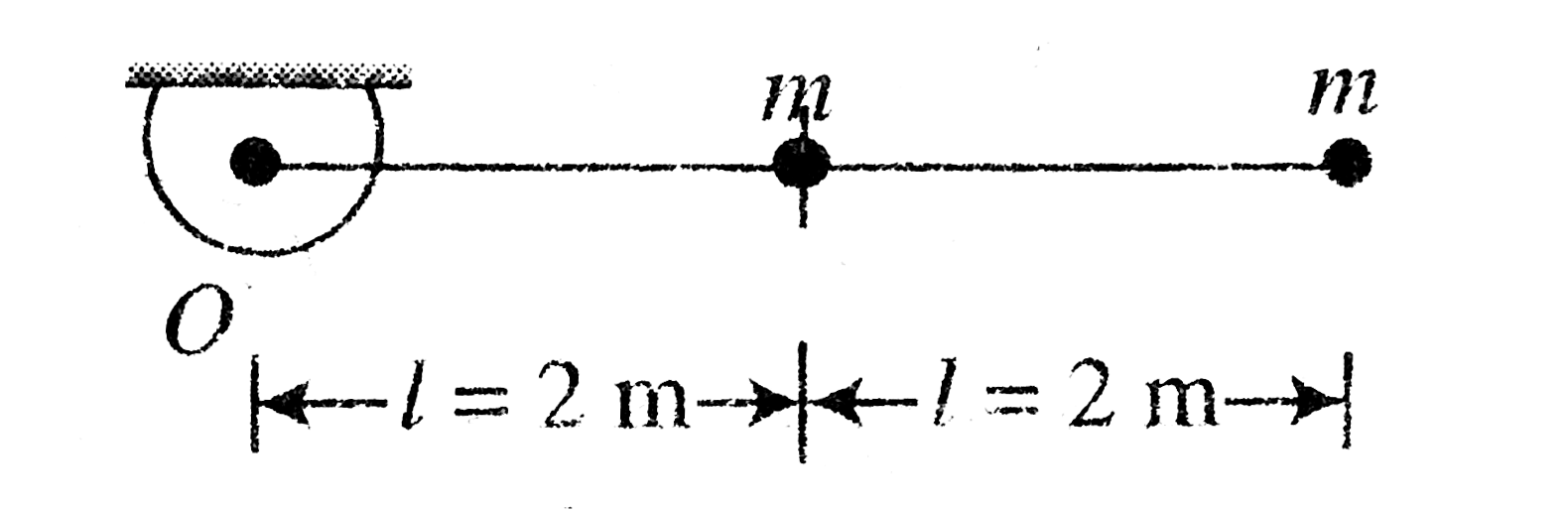
reaction offered by the pivot at t=0 (in N).
View SolutionA uniform rod smoothly pivoted at one of its ends is released from rest. If it swings in vertical plane, the maximum speed of the end P of the rod is.
 .
.
View SolutionA uniform rod of mass m and length / is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity vo collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
View SolutionA uniform rod of length 75cm is hinged at one of its ends and is free to rotate in vertical plane. It is released from rest when rod is horizontal. When the rod becomes vertical, it is breaks at mid− point and lower part now moves freely. The distance of centre of lower part from hinge, when it again becomes vertical for the first time is r. Find the approximate value of 2r.
View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is

View SolutionAB is a mass less rigid rod of length 2l. It is free to rotate in vertical plane about a horizontal axis passing through its end A. Equal point masses (m each) are stuck at the centre C and end Bof the rod. The rod is released from horizontal position. Write the tension in the rod when it becomes vertical.

View SolutionA uniform rod of mass m and length L is hinged about one end and can freely rotate in a vertical plane. The angular velocity of the rod, when it falls from position P to Q. through an angle α starting from rest, is

View Solution