In the arrangement shown in figure, the track is frictionless until the body reaches the higher level. A frictional force stops the body in a distance d from A. The initial speed of the body v0 is 6 m/s the height h is 1 m and the coefficient of kinetic friction is 0.2. What is the maximum distance d travelled by body on rough surface?
3 m
4 m
5 m
4.25 m
The correct Answer is:B
To solve the problem step by step, we will use the principles of conservation of energy and the work-energy theorem.
Step 1: Calculate the final velocity (V) at point A using conservation of energy.
The initial kinetic energy (KE_initial) and potential energy (PE_initial) at the starting point (point B) can be expressed as:
- KE_initial = 12mv20
- PE_initial = 0 (since we are taking the reference level at point B)
At point A, the body has kinetic energy (KE_final) and potential energy (PE_final):
- KE_final = 12mV2
- PE_final = mgh (where h is the height)
Using conservation of energy:
KEinitial+PEinitial=KEfinal+PEfinal
Substituting the values:
12mv20+0=12mV2+mgh
We can cancel mass (m) from both sides:
12v20=12V2+gh
Now substituting v0=6m/s, g=10m/s2, and h=1m:
12(62)=12V2+10⋅1
18=12V2+10
Rearranging gives:
12V2=18−10
12V2=8
V2=16
V=4m/s
Step 2: Calculate the distance (d) traveled on the rough surface.
The work done against friction (W_friction) is equal to the change in kinetic energy as the body comes to rest:
Wfriction=KEinitial−KEfinal
Since the body comes to rest, KEfinal=0:
Wfriction=KEinitial
The initial kinetic energy at point A is:
KEinitial=12mV2
Substituting V=4m/s:
KEinitial=12m(42)=12m(16)=8m
The work done against friction can also be expressed as:
Wfriction=Ffriction⋅d
Where Ffriction=μmg (with μ=0.2):
Ffriction=0.2mg
Thus, we have:
8m=0.2mg⋅d
Cancelling m from both sides (assuming m≠0):
8=0.2g⋅d
Substituting g=10m/s2:
8=0.2⋅10⋅d
8=2d
d=82=4m
Final Answer:
The maximum distance d traveled by the body on the rough surface is 4 meters.
---
The initial kinetic energy (KE_initial) and potential energy (PE_initial) at the starting point (point B) can be expressed as:
- KE_initial = 12mv20
- PE_initial = 0 (since we are taking the reference level at point B)
- KE_final = 12mV2
- PE_final = mgh (where h is the height)
KEinitial+PEinitial=KEfinal+PEfinal
12mv20+0=12mV2+mgh
12v20=12V2+gh
12(62)=12V2+10⋅1
18=12V2+10
12V2=18−10
12V2=8
V2=16
V=4m/s
The work done against friction (W_friction) is equal to the change in kinetic energy as the body comes to rest:
Wfriction=KEinitial−KEfinal
Since the body comes to rest, KEfinal=0:
Wfriction=KEinitial
KEinitial=12mV2
Substituting V=4m/s:
KEinitial=12m(42)=12m(16)=8m
Wfriction=Ffriction⋅d
Where Ffriction=μmg (with μ=0.2):
Ffriction=0.2mg
8m=0.2mg⋅d
8=0.2g⋅d
8=0.2⋅10⋅d
8=2d
d=82=4m
The maximum distance d traveled by the body on the rough surface is 4 meters.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-D (LINKED COMPREHENSION TYPE QUESTIONS) (COMPREHENSION-IV)
3 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-E (ASSERTION-REASON TYPE QUESTIONS)
9 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-D (LINKED COMPREHENSION TYPE QUESTIONS) (COMPREHENSION-II)
3 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
In the arrangement show in figure, the track is frictionless until the body reaches the higher level. A frictional force stops the body in a distance d from A. The initial speed of the body v0 is 6 m/s the height h is 1 m and the coefficient of kinetic friction is 0.2.
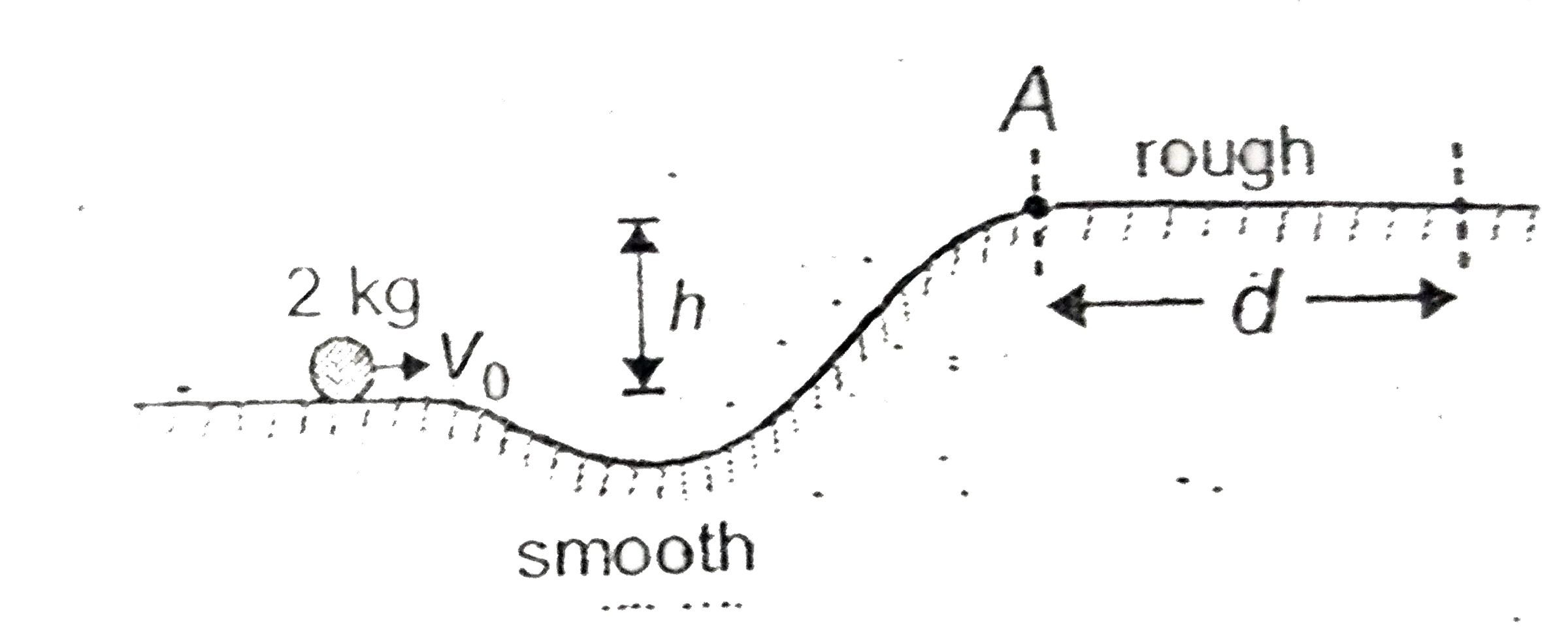
The speed of body at the higher level A is
View SolutionIn the arrangement show in figure, the track is frictionless until the body reaches the higher level. A frictional force stops the body in a distance d from A. The initial speed of the body v0 is 6 m/s the height h is 1 m and the coefficient of kinetic friction is 0.2.
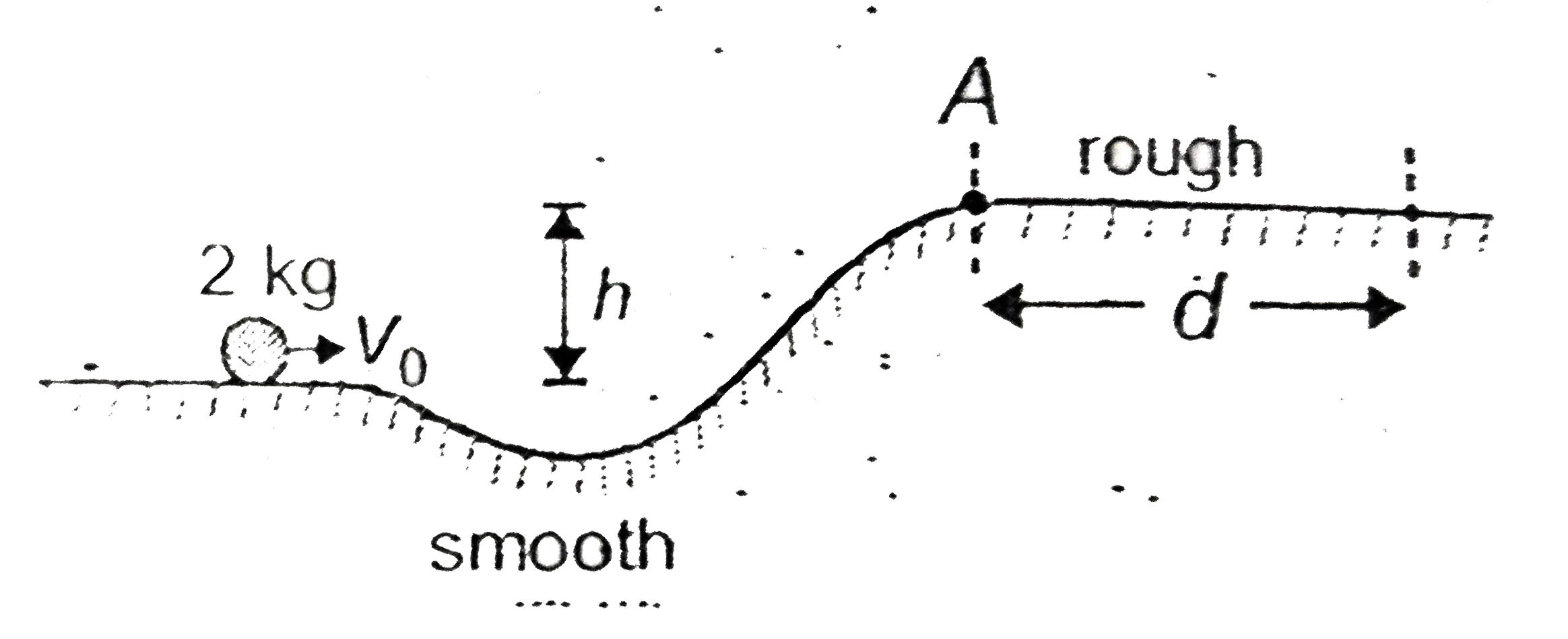
What is the work done by friction force on the body during the motion.
View SolutionFigure, a block slides along a track from one level to a higher level by moving through an intermediate valley. The track is friction less until the block reaches the higher
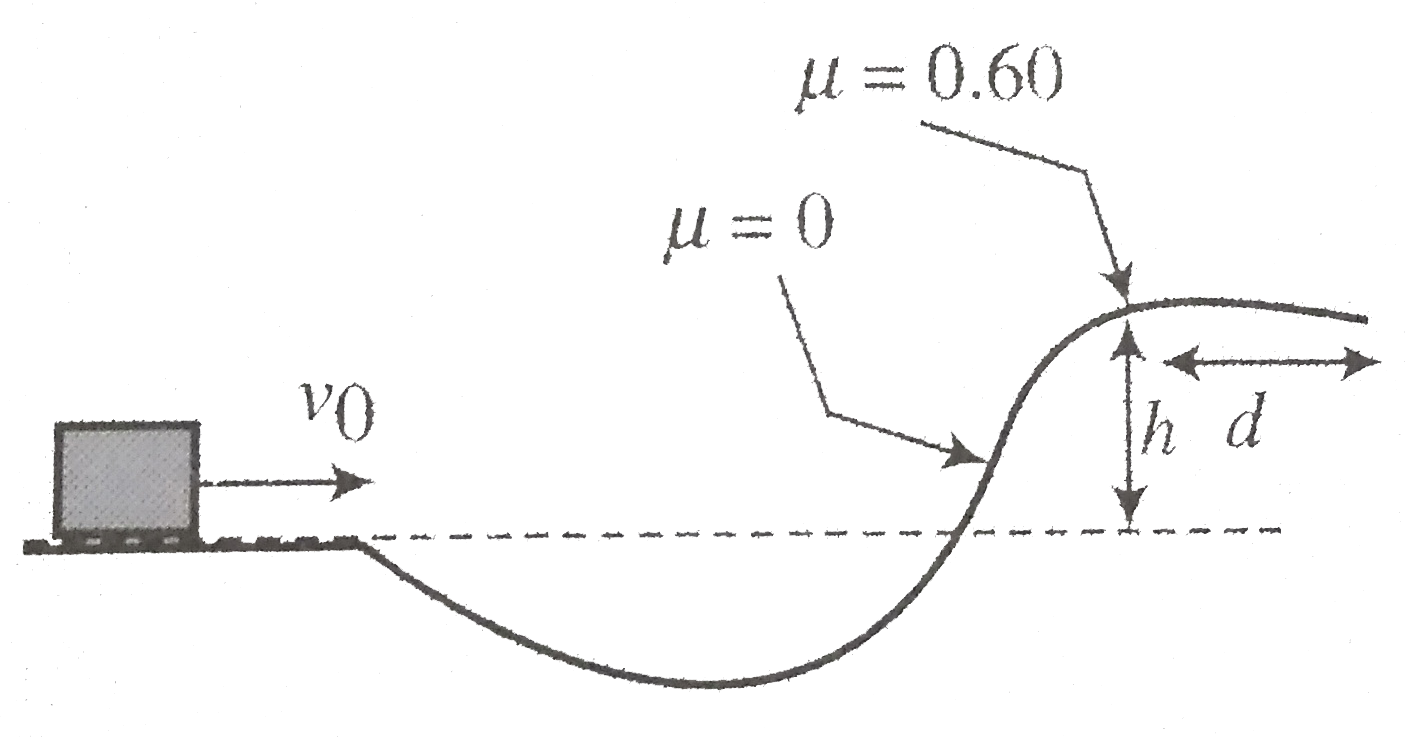 level. Then there is friction force which stops the block at a distance d. The block's initial speed v0 is 6.0ms−1, the height difference h is 1.1m, and the coefficient of kinetic friction μ is 0.60. Find d.
level. Then there is friction force which stops the block at a distance d. The block's initial speed v0 is 6.0ms−1, the height difference h is 1.1m, and the coefficient of kinetic friction μ is 0.60. Find d.
View SolutionIf a body has kinetic energy. T, moving on a rough horizontal surface stops at distance y. The frictional force exerted on the body is
View SolutionA body moving with a speed of 54kmph is brought to rest in a distances. If the coefficient of friction between the body and the surface is 0.3. Calculate the distance travelled by the body ?
View SolutionA block is pushed up a rough inclined plane of 45°. If the time of descent is twice the time of ascent, the coefficient of friction is
View SolutionA body is moving along a rough horizontal surface with an initial velocity 6m/s m If the body comes to rest after travelling 9 m , then the coefficient of sliding friction will be
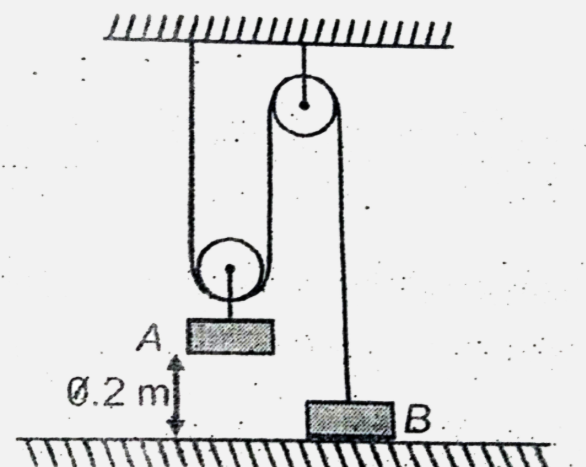
View SolutionIn the arrangment shown in figure , the mass of the body A is 4 m and that of body B is m . The height h=0⋅2 m . If the body B is released , then till what maximum height the body B will go up ? (g = 10m/s2)
View SolutionA body slipping on a rough horizontal plane moves wioth a deceleationof 4.0ms. What is cofficient of kineic friction between the block and the plane?
View SolutionA body of mass 2kg collides with a horizontal weight spring of force constant 4Nm−1. The body compresses the spring by 1m from rest position. Find the speed of the block at the instant of collision ? Given that the coefficient of kinetic friction between the body and the surface is 0.1.
View Solution
