A square plate of side 'a' and mass 'm' is lying on a horizontal floor. A force F is applied at the top. Find the maximum force that can be applied on the square plate so that the plate does not topple about A.
To solve the problem of finding the maximum force F that can be applied to a square plate of side a and mass m without causing it to topple about point A, we will follow these steps:
Step 1: Understand the Forces Acting on the Plate
The forces acting on the plate include:
- The gravitational force mg acting downward at the center of mass.
- The normal force N acting upward at the base.
- The applied force F acting horizontally at the top of the plate.
- The frictional force f acting horizontally at the base, opposing the applied force.
Step 2: Set Up the Equations
1. Vertical Forces: The normal force N balances the weight of the plate:
N=mg(Equation 1)
2. Horizontal Forces: The applied force F is balanced by the frictional force f:
F=f(Equation 2)
Step 3: Analyze the Torque
To prevent the plate from toppling about point A, the net torque about point A must be zero. The torque due to the applied force F and the frictional force f must balance the torque due to the weight of the plate.
1. The distance from point A (the pivot) to the center of mass (which is at a distance a2 from A) is a2.
2. The torque due to the applied force F is:
τF=F⋅a2
3. The torque due to the weight mg about point A is:
τmg=mg⋅a2
Step 4: Set Up the Torque Equation
For the plate not to topple:
F⋅a2=mg⋅a2
Step 5: Solve for the Maximum Force F
Cancelling a2 from both sides gives:
F=mg
Step 6: Consider the Friction
Since the frictional force f must also be equal to the applied force F (from Equation 2), we can substitute F into the equation:
F=mg2
Thus, the maximum force that can be applied on the square plate so that the plate does not topple about point A is:
mg2
The forces acting on the plate include:
- The gravitational force mg acting downward at the center of mass.
- The normal force N acting upward at the base.
- The applied force F acting horizontally at the top of the plate.
- The frictional force f acting horizontally at the base, opposing the applied force.
1. Vertical Forces: The normal force N balances the weight of the plate:
N=mg(Equation 1)
F=f(Equation 2)
To prevent the plate from toppling about point A, the net torque about point A must be zero. The torque due to the applied force F and the frictional force f must balance the torque due to the weight of the plate.
2. The torque due to the applied force F is:
τF=F⋅a2
3. The torque due to the weight mg about point A is:
τmg=mg⋅a2
For the plate not to topple:
F⋅a2=mg⋅a2
Cancelling a2 from both sides gives:
F=mg
Since the frictional force f must also be equal to the applied force F (from Equation 2), we can substitute F into the equation:
F=mg2
mg2
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)62videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - B) Objective Type Questions (One option is correct)60videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Try Yourself63videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE21videos
TEST 1
Similar Questions
A uniform square block of side 'a' and mass 'm' is lying on a horizontal surface. A small block of mass m is placed on the top block. Find the distance by which normal reaction is shifted.
 View Solution
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View Solution
Knowledge Check
- Question 1 - Select One
A block A of mass 4 kg is placed on another block B of mass 5 kg and the block rests on a smooth horizontal table. For sliding the block A on B, a horizontal force of 12 N is required to be applied on it. The maximum horizontal force that can be applied on B so that both A and B move together and the acceleration produced by this force is
 A25 N, 5 m/s2B27 N, 3 m/s2C30 N, 8 m/s2Dcannot be calculated from the given data.
A25 N, 5 m/s2B27 N, 3 m/s2C30 N, 8 m/s2Dcannot be calculated from the given data.
12N of force required to be applied on A to slip on B. Find the maximum horizontal force F to be applied on B so that A and B moves together.
 View Solution
View SolutionA uniform cube of side 'a' and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly below the centre of the face, at a height a/4 above the base.
a. What is the minimum value of F for which the cube begins to tip about an edge?
b. What is the minimum value of its so that toppling occurs?
c. If μ=μmin find minimum force for topping.
d. Find minimum μs so that Fmin can cause toppling.View SolutionThree identical cubes each of mass m are place on a smooth horizontal surface.A constant force F is applied on A as shown in the figure.The force on B applied by C is
View SolutionUniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force is applied at the top point P of the cylinder so that it start pure rolling .In the above question, the frictional force on the cylinder is
View Solution
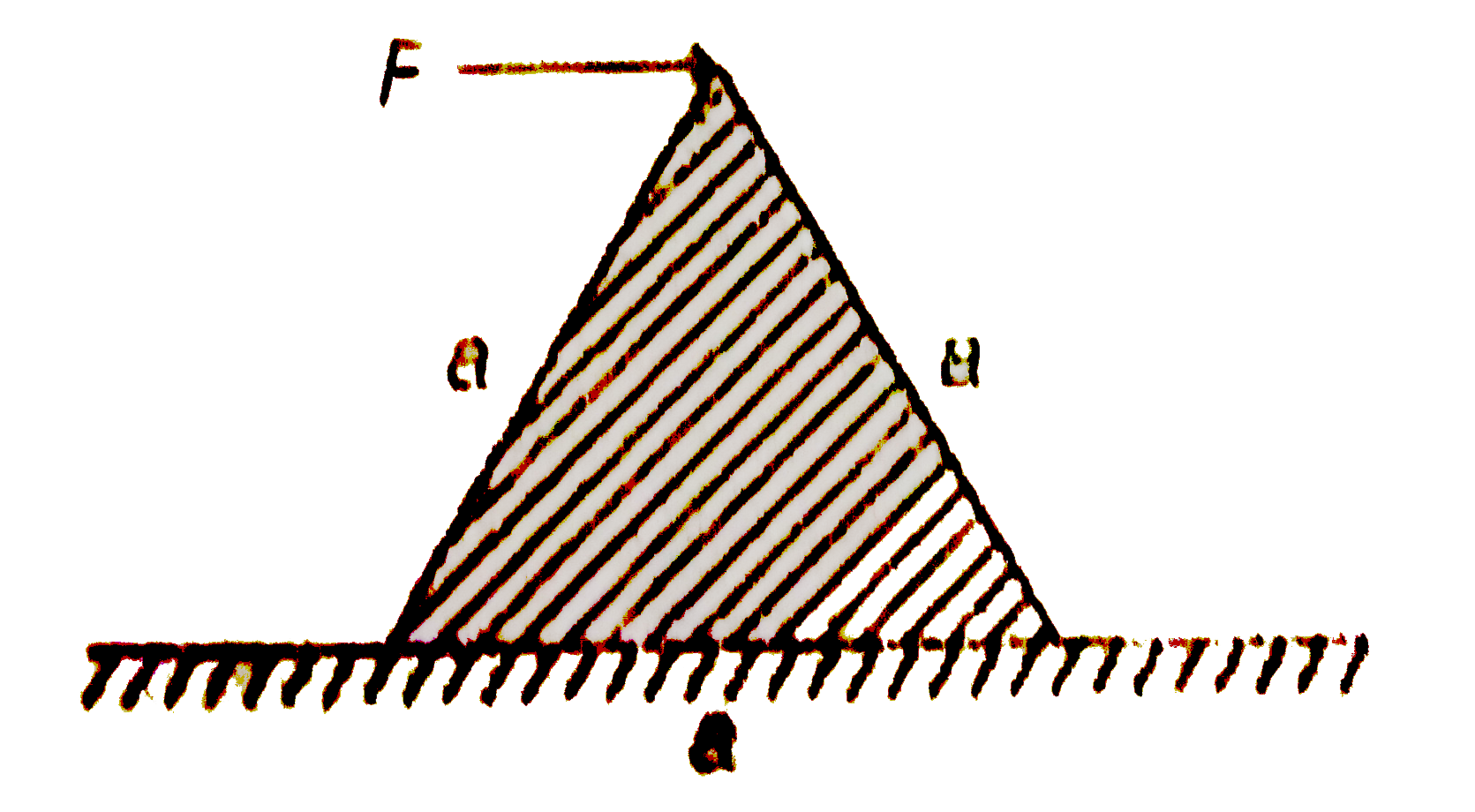
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isView SolutionAn equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
 View Solution
View SolutionAs shown in figure, if we apply a horizontal force F on the block, find the maximum force F (in N) that can be applied so that block does not slide up. (Givenθ=45∘,g=10m/sec2,m=15kg,μ=12)
 View Solution
View Solution

