If a diaelectric material of dielectric constant is completely filled between two point charges as shown in the figure, then the net electrostatic force on is
zero
To find the net electrostatic force on charge q1 when a dielectric material with dielectric constant ϵr is completely filled between two point charges q1 and q2, we can follow these steps:
Step 1: Understand the Electrostatic Force Formula
The electrostatic force F between two point charges q1 and q2 separated by a distance r in a vacuum is given by Coulomb's law:
F=kq1q2r2
where k is Coulomb's constant, which can also be expressed as:
k=14πϵ0
Thus, the formula can be rewritten as:
F=14πϵ0q1q2r2
Step 2: Effect of Dielectric Material
When a dielectric material with dielectric constant ϵr is introduced between the charges, the electrostatic force is reduced by a factor of ϵr. Therefore, the new force F′ can be expressed as:
F′=Fϵr
Step 3: Substitute the Original Force
Substituting the expression for F into the equation for F′:
F′=1ϵr(14πϵ0q1q2r2)
Step 4: Simplify the Expression
This simplifies to:
F′=14πϵ0ϵrq1q2r2
Step 5: Final Expression
Thus, the net electrostatic force on charge q1 when the dielectric material is present is given by:
F′=14πϵ0ϵrq1q2r2
Conclusion
The net electrostatic force on q1 is:
F′=14πϵ0ϵrq1q2r2
The electrostatic force F between two point charges q1 and q2 separated by a distance r in a vacuum is given by Coulomb's law:
F=kq1q2r2
where k is Coulomb's constant, which can also be expressed as:
k=14πϵ0
Thus, the formula can be rewritten as:
F=14πϵ0q1q2r2
When a dielectric material with dielectric constant ϵr is introduced between the charges, the electrostatic force is reduced by a factor of ϵr. Therefore, the new force F′ can be expressed as:
F′=Fϵr
Substituting the expression for F into the equation for F′:
F′=1ϵr(14πϵ0q1q2r2)
This simplifies to:
F′=14πϵ0ϵrq1q2r2
Thus, the net electrostatic force on charge q1 when the dielectric material is present is given by:
F′=14πϵ0ϵrq1q2r2
The net electrostatic force on q1 is:
F′=14πϵ0ϵrq1q2r2
Topper's Solved these Questions
Similar Questions
In the figure shown P2andP2 are two conducting plates having charges of equal magnitude and opposite sign. Two dielectrics of dielectric constant K1andK2 fill the space between the plates as shown in the figure. The ratio of electrical energy in 1st dielectric to that in the 2nd dielectric is :

View SolutionA parallel plate capacitor has a dielectric slab of dielectric constant K between its plates that covers 1/3 of the area of its plates, as shown in the figure. The total capacitance of the capacitor is C while that of the portion with dielectric in between is C1. When the capacitor is charged, the plate area covered by the dielectric gets charge Q1 and the rest of the area gets charge Q2. The electric field in the dielectric is E1 and that in the other portion is E2. Choose the correct option/options, ignoring edge effects.

View SolutionIf →a and →b are two unit vectors and θ is the angle between them, then the unit vector along the angular bisector of →a and →b will be given by
View Solution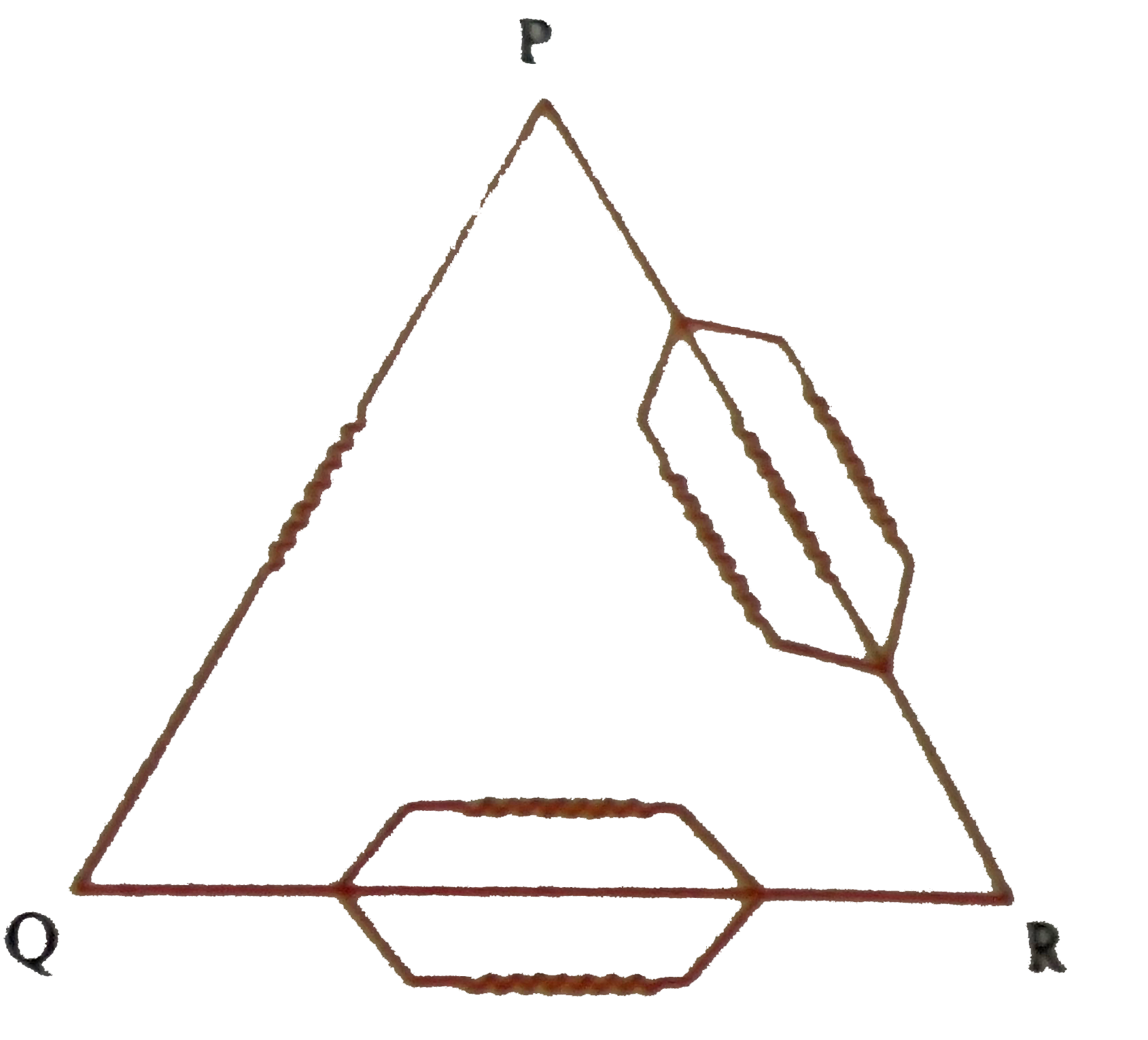
Six equal resistances are connected between points P, Q and R as shown in the figure. Then the net resistance will be maximum between
View SolutionTwo similar point charges q1andq2 are placed at a distance r apart in the air. The force between them is F1 . A dielectric slab of thickness t(<r) and dielectric constant K is placed between the charges . Then the force between the same charge . Then the fore between the same charges is F2 . The ratio is
View SolutionForce between two identical charges placed at a distance of r in vacuum is F.Now a slab of dielectric constant 4 is inserted between these two charges . If the thickness of the slab is r/2, then the force between the charges will becomes
View SolutionAir filled capacitor of capacitance 2μF is filled with three dielectric material of dielectric constant K1=4,K2=4 and K3=6 as shown in the figure . The new capacitance of the capacitor is
View SolutionAssertion : When two positive point charges move away from each other, then their electrostatic potential energy decreases.
Reason : Change in potential energy between two points is equal to the work done by electrostatic forces.
View SolutionThe net resistance between points P and Q in the circuit shown in figure is

View SolutionForce between two conducting large plates , with charges Q and Q2 as shown in the figure, is (Area of each face of plate =A)
_PHY_E01_022_Q01.png)
View Solution
