A planet is at R distance from sun and its time period of revolution is T. What will be its new time period of revolution if it brought 0.5 R distance closer to sun ?
4T√2
√2T4
2√2T
√2T
The correct Answer is:B
To solve the problem, we will use Kepler's Third Law of Planetary Motion, which states that the square of the time period of revolution (T) of a planet is directly proportional to the cube of the semi-major axis of its orbit (R). Mathematically, this can be expressed as:
T2∝R3
1. Identify the Given Values:
- Initial distance from the sun, R1=R
- Initial time period of revolution, T1=T
- New distance from the sun, R2=R−0.5R=0.5R
2. Apply Kepler's Third Law:
According to Kepler's law, we can write:
T21R31=T22R32
3. Substitute the Known Values:
Substitute R1=R and R2=0.5R:
T2R3=T22(0.5R)3
4. Simplify the Right Side:
Calculate (0.5R)3:
(0.5R)3=0.125R3=18R3
So the equation becomes:
T2R3=T2218R3
5. Cross-Multiply to Solve for T22:
T2⋅18R3=T22⋅R3
Dividing both sides by R3 gives:
T28=T22
6. Solve for T2:
Taking the square root of both sides:
T2=√T28=T√8=T2√2
7. Final Expression:
We can express T2 as:
T2=√24T
Conclusion:
The new time period of revolution when the planet is brought 0.5R closer to the sun is:
T2=√24T
- Initial distance from the sun, R1=R
- Initial time period of revolution, T1=T
- New distance from the sun, R2=R−0.5R=0.5R
According to Kepler's law, we can write:
T21R31=T22R32
Substitute R1=R and R2=0.5R:
T2R3=T22(0.5R)3
Calculate (0.5R)3:
(0.5R)3=0.125R3=18R3
So the equation becomes:
T2R3=T2218R3
T2⋅18R3=T22⋅R3
Dividing both sides by R3 gives:
T28=T22
Taking the square root of both sides:
T2=√T28=T√8=T2√2
We can express T2 as:
T2=√24T
The new time period of revolution when the planet is brought 0.5R closer to the sun is:
T2=√24T
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -B (Objective Type Questions (one option is correct))
20 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -C (Objective Type Questions (More than one option are correct))
12 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - Try Yourself
33 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
Time period of revolution of polar satellite is around
View SolutionThe period of revolution of a satellite in an orbit of radius 2R is T. What will be its period of revolution in an orbit of radius 8R ?
View SolutionA body is projected from earth's surface to become its satellite, its time period of revolution will not depend upon
View SolutionThe Earth and Jupiter are two planets of the sun. The orbital radius of the earth is 107m and that of Jupiter is 4×107m If the time period of revolution of earth is T=365 days find time period of revolution of the Jupiter
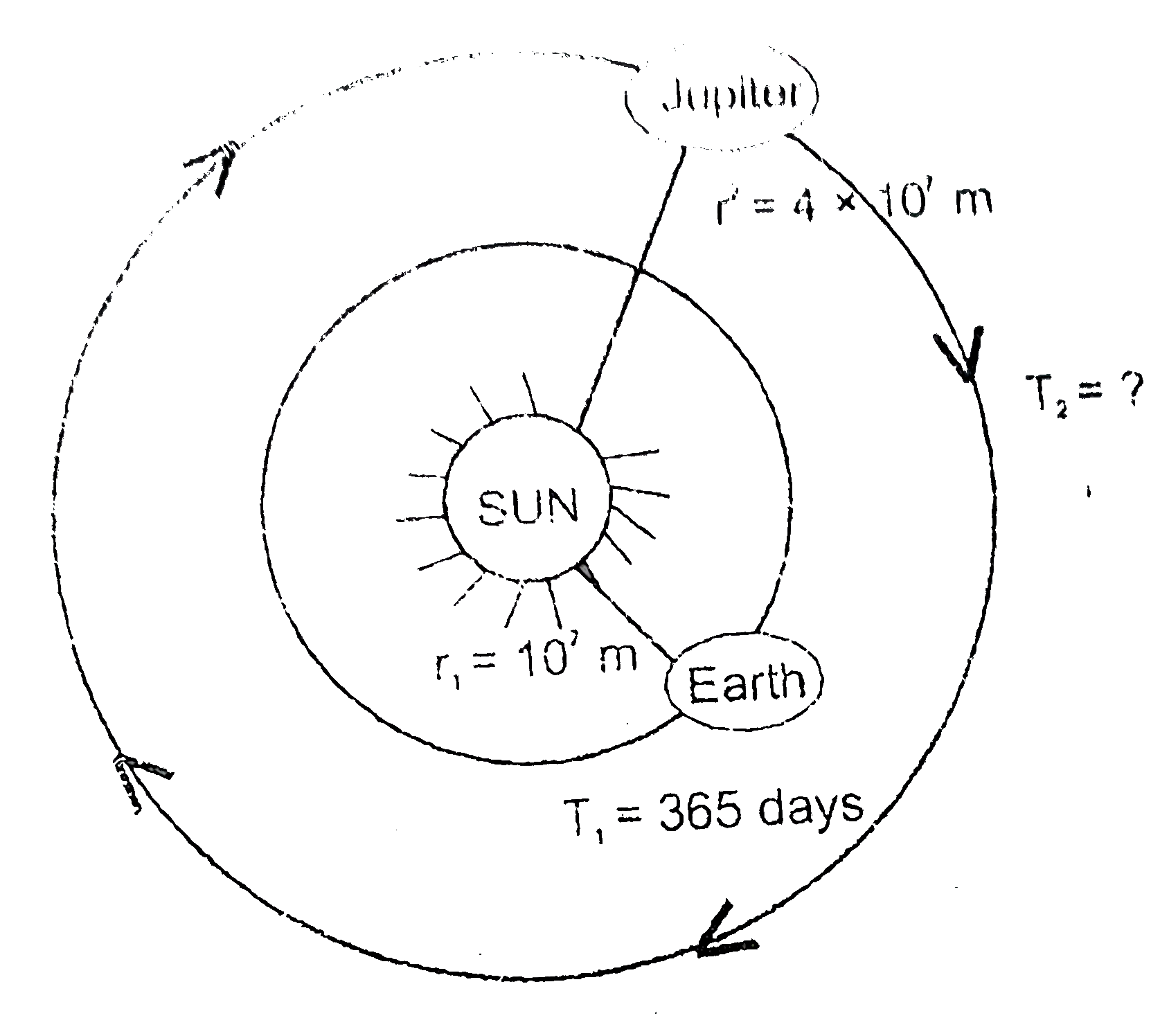 .
.
View SolutionA particle moves in a circle of radius R. In half the period of revolution its displacement is ………… and distance covered is ………. .
View SolutionThe distance of the planet Jupiter from the Sun is 5.2 times that of the Earth. Find the period of Jupiter's revolution around the Sun.
View SolutionNear the earth's surface time period of a satellite is 4 hrs. Find its time period if it is at the distance '4R' from the centre of earth :-
View SolutionTwo satellite of mass m and 9m are orbiting a planet in orbits of radius R. Their periods of revolution will be in the ratio of
View SolutionFor a satellite orbiting close to the surface of earth the period of revolution is 84min. The time period of another satellite orbiting at a height three times the radius of earth from its surface will be
View SolutionThe radius of a planet is R1 and a satellite revolves round it in a circle of radius R2. The time period of revolution is T. find the acceleration due to the gravitation of the plane at its surface.
View Solution
