The gravitational potential energy of a system of three particles of mass m each kept at the vertices of equilateral triangle of side x will be
−Gm2x
−Gm23x
−3Gm2x
3Gm2x2
The correct Answer is:C
To find the gravitational potential energy of a system of three particles of mass m each, placed at the vertices of an equilateral triangle with side length x, we can follow these steps:
Step 1: Understand the System
We have three particles, each of mass m, located at the vertices of an equilateral triangle. Let's label the vertices as A, B, and C.
Step 2: Write the Formula for Gravitational Potential Energy
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by the formula:
U=−Gm1m2r
where G is the gravitational constant.
Step 3: Calculate the Potential Energy Between Each Pair of Masses
1. Potential Energy between Masses at A and B:
UAB=−Gmmx=−Gm2x
2. Potential Energy between Masses at B and C:
UBC=−Gmmx=−Gm2x
3. Potential Energy between Masses at C and A:
UCA=−Gmmx=−Gm2x
Step 4: Sum the Potential Energies
The total gravitational potential energy U of the system is the sum of the potential energies of each pair:
U=UAB+UBC+UCA
Substituting the values we calculated:
U=−Gm2x−Gm2x−Gm2x
U=−3Gm2x
Final Answer
Thus, the gravitational potential energy of the system of three particles is:
U=−3Gm2x
We have three particles, each of mass m, located at the vertices of an equilateral triangle. Let's label the vertices as A, B, and C.
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by the formula:
U=−Gm1m2r
where G is the gravitational constant.
1. Potential Energy between Masses at A and B:
UAB=−Gmmx=−Gm2x
UBC=−Gmmx=−Gm2x
UCA=−Gmmx=−Gm2x
The total gravitational potential energy U of the system is the sum of the potential energies of each pair:
U=UAB+UBC+UCA
Substituting the values we calculated:
U=−Gm2x−Gm2x−Gm2x
U=−3Gm2x
Thus, the gravitational potential energy of the system of three particles is:
U=−3Gm2x
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -B (Objective Type Questions (one option is correct))
20 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -C (Objective Type Questions (More than one option are correct))
12 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - Try Yourself
33 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
The gravitational potential energy of an isolated system of three particles, each of mass m, at the three corners of an equilateral triangle of side l is
View SolutionFind the potential energy of a system of 3 particles kept at the vertices of an equilateral triangle of side r.
View SolutionFind the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
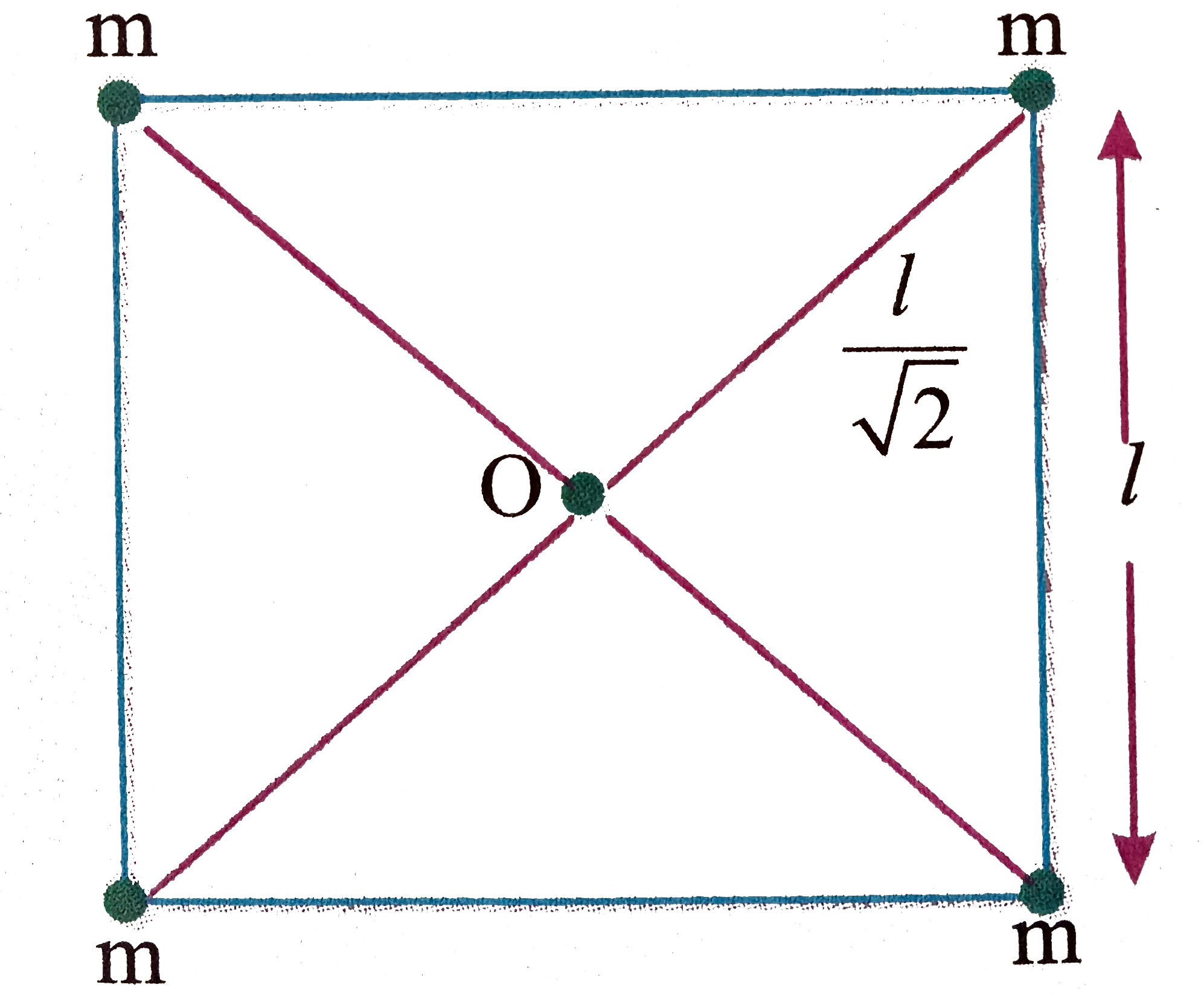
View SolutionThe position co-ordinates of the centre of mass of a system of three particles of equal masses which are placed on the verctices of an equilateral triangle of a side a are shown. Locate centre mass?

View SolutionFind the potential energy of a system of four particles each of mass 2m kept at the vertices of a square of side x. Also find the potential at the centr of the square.
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThe gravitational potential at the centre of a square of side a when four point masses m each are kept at its vertices will be
View SolutionFind the potential energy of a system of eight particles of mass M placed at the vertices of a cube of side L. neglect the self energy of the particles.
View SolutionFind the area of an equilateral triangle having each side x cm
View SolutionFind the potential energy of 4-particles, each of mass 1 kg placed at the four vertices of a square of side length 1 m.
View Solution
