Find the gravitational potential energy of a system of four particles, each of mass $m$ placed at the verticles of a square of side $l$ . Also obtain the gravitaitonal potential at centre of the square.

Video Solution

Text Solution

Verified by Experts

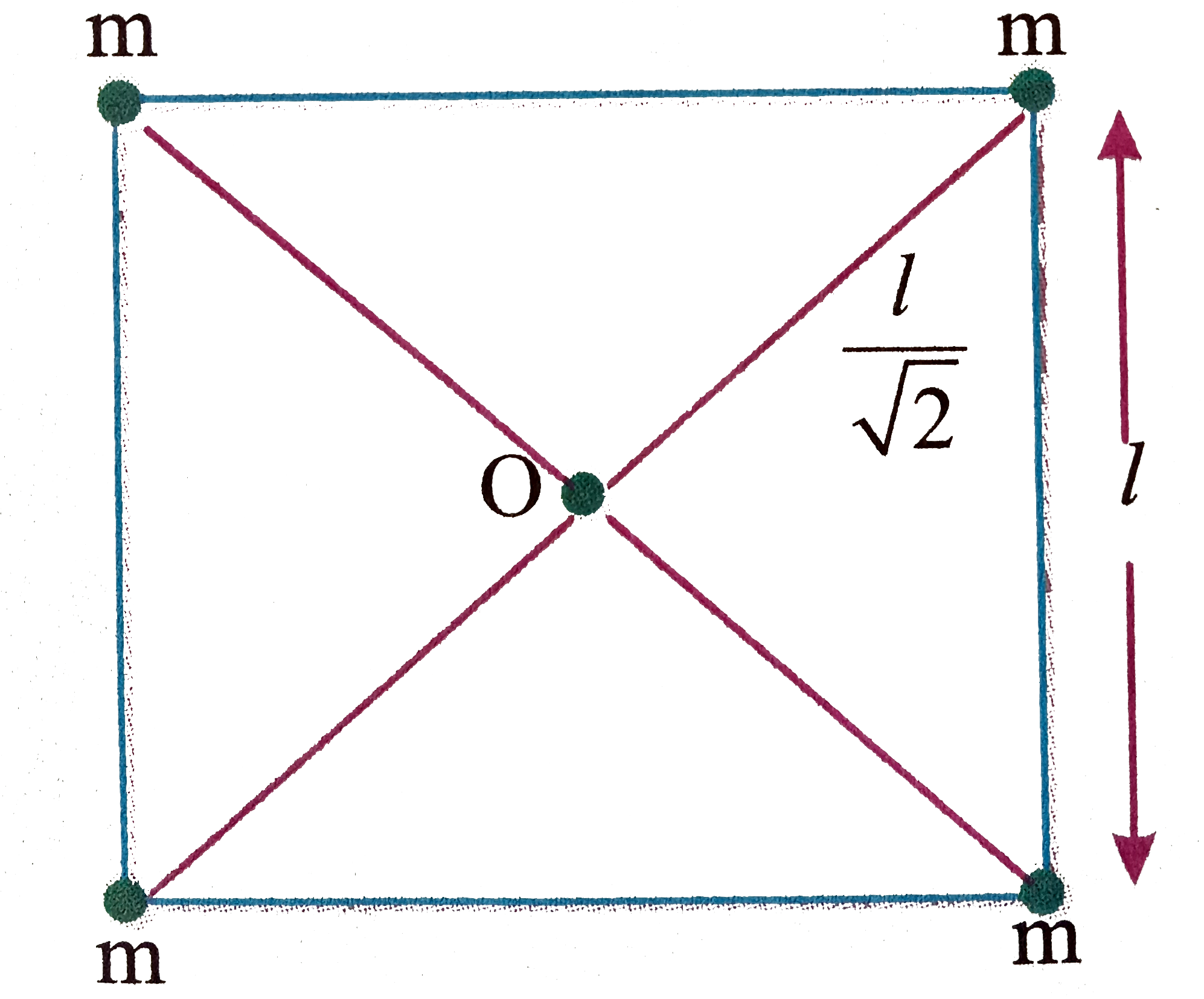
Consider four masses each of mass m at the corners of a square of side l: See Fig. ,9. We have four mass paris at distance l and two diagonal pairs at distance $\sqrt{2} l$
Hence,
$W ® = - 4 \frac{G m^{2}}{l} - 2 \frac{G m^{2}}{\sqrt{2} l}$

$= - \frac{2 G m^{2}}{l} (2 + \frac{1}{\sqrt{2}}) = - 5.41 \frac{G m^{2}}{l}$
The gravitational potential at the centre of the square $(r = \sqrt{2} l / 2)$ is
$U (r) = - 4 \sqrt{2} \frac{G m}{l}$

Updated on:21/07/2023

Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A $- \frac{\sqrt{2} G m^{2}}{l} (2 - \frac{1}{\sqrt{2}})$
B $- \frac{2 G m^{2}}{l} (2 + \frac{1}{\sqrt{2}})$
C $- \frac{\sqrt{2} G m^{2}}{l} (\sqrt{2} - \frac{1}{\sqrt{2}})$
D $- \frac{2 G m^{2}}{l} (\sqrt{2} - \frac{1}{\sqrt{2}})$