Given that the gravitation potential on Earth surface is V0. The potential at a point distant half the radius of earth from the cetre will be
114V0
V02
2V0
118V0
The correct Answer is:D
To find the gravitational potential at a point that is half the radius of the Earth from the center, we can follow these steps:
Step 1: Understand the gravitational potential at the Earth's surface
The gravitational potential V0 at the surface of the Earth is given by the formula:
V0=−GMR
where:
- G is the universal gravitational constant,
- M is the mass of the Earth,
- R is the radius of the Earth.
Step 2: Use the formula for gravitational potential inside a sphere
The gravitational potential V at a distance r from the center of a uniform sphere (where r<R) is given by:
V=−GM2R3(3R2−r2)
Step 3: Substitute r=R2
We need to find the potential at a point that is half the radius of the Earth from the center, so we set r=R2:
V=−GM2R3(3R2−(R2)2)
Step 4: Simplify the expression
Calculating (R2)2:
(R2)2=R24
Now substituting this back into the potential formula:
V=−GM2R3(3R2−R24)
Combine the terms inside the parentheses:
3R2−R24=12R24−R24=11R24
So, we have:
V=−GM2R3⋅11R24
Step 5: Further simplify the expression
This simplifies to:
V=−11GM8R3
Step 6: Relate this to V0
We know from Step 1 that:
V0=−GMR
Thus, we can express V in terms of V0:
V=118⋅V0
Final Result
The gravitational potential at a point distant half the radius of the Earth from the center is:
V=118V0
The gravitational potential V0 at the surface of the Earth is given by the formula:
V0=−GMR
where:
- G is the universal gravitational constant,
- M is the mass of the Earth,
- R is the radius of the Earth.
The gravitational potential V at a distance r from the center of a uniform sphere (where r<R) is given by:
V=−GM2R3(3R2−r2)
We need to find the potential at a point that is half the radius of the Earth from the center, so we set r=R2:
V=−GM2R3(3R2−(R2)2)
Calculating (R2)2:
(R2)2=R24
Now substituting this back into the potential formula:
V=−GM2R3(3R2−R24)
Combine the terms inside the parentheses:
3R2−R24=12R24−R24=11R24
So, we have:
V=−GM2R3⋅11R24
This simplifies to:
V=−11GM8R3
We know from Step 1 that:
V0=−GMR
Thus, we can express V in terms of V0:
V=118⋅V0
The gravitational potential at a point distant half the radius of the Earth from the center is:
V=118V0
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -C (Objective Type Questions (More than one option are correct))
12 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -D (Linked Comprehension Type Questions)
13 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -A (Objective Type Questions (one option is correct))
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
If V is the gravitational potential on the surface of the earth, then what is its value at the centre of the earth ?
View SolutionIf a charged spherical conductor of radius 5 cm has potential V at a point distant 5 cm its centre, then the potential at a point distant 30 cm from the centre will be
View Solution
Knowledge Check
A body weighs 72 N on the surface of the earth. What is the gravitational force on it due to earth at a height equal to half the radius of the earth from the surface
A16 NB28 NC32 ND72 N
If a charged spherical conductor of radius 10cm has potential V at a point distant 5cm from its centre, then the potential at a point distant 15cm from the centre will be
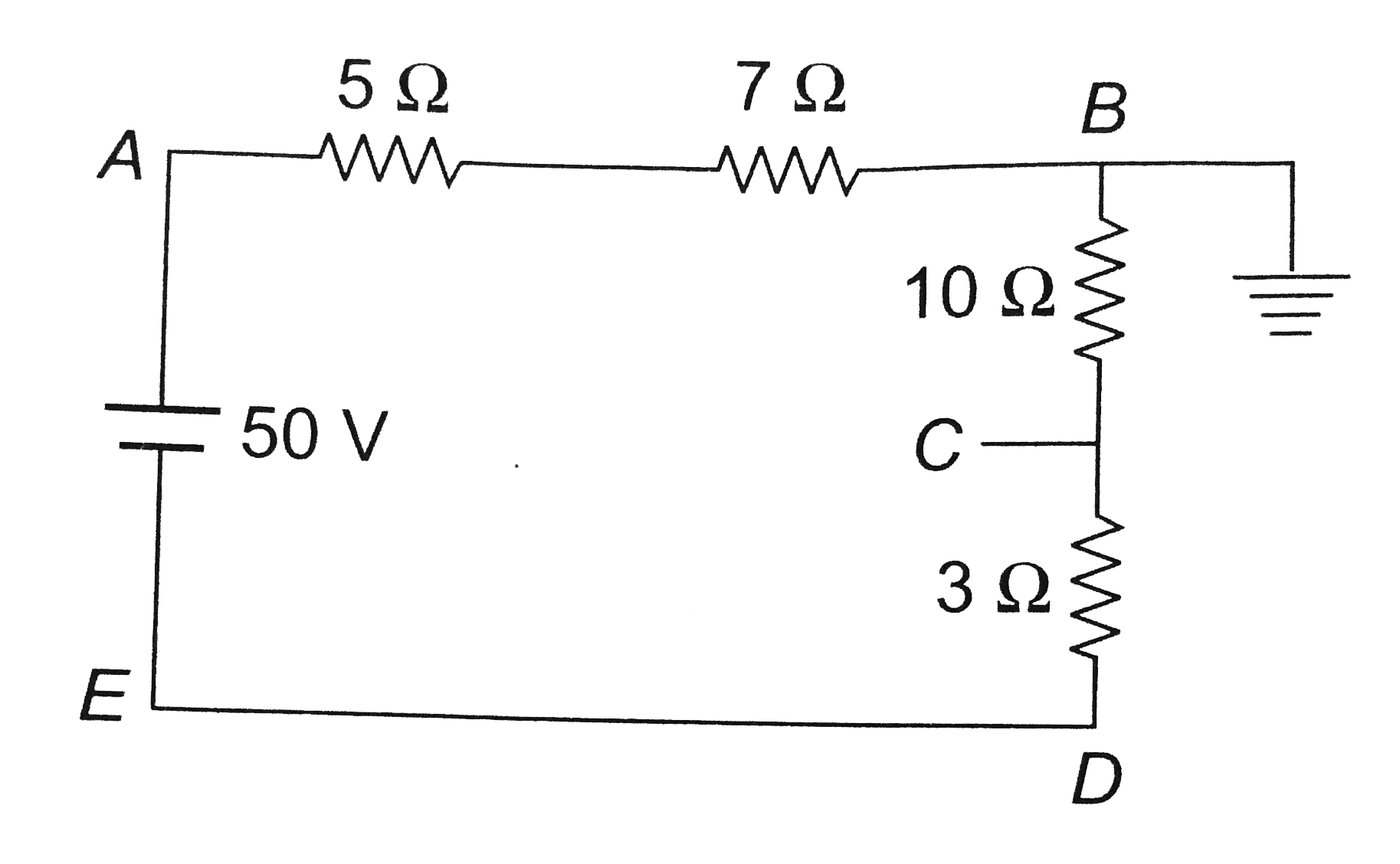
View SolutionIn the circuit shown, the point B is earthed. The potential at the point 'A' is
View SolutionA body weighs 63 N on the surface of the earth. What is the gravitational force on it due to the earth at a height equal to half the radius of the earth ?
View SolutionA body weighs 63 N on the surface of the earth. What is the gravitational force on it due to the earth at a height equal to half the radius of the earth ?
View SolutionA satellite of mass m is revolving around the Earth at a height R above the surface of the Earth. If g is the gravitational intensity at the Earth’s surface and R is the radius of the Earth, then the kinetic energy of the satellite will be:
View SolutionA satellite of mass m is revolving around the Earth at a height R above the surface of the Earth. If g is the gravitational intensity at the Earth’s surface and R is the radius of the Earth, then the kinetic energy of the satellite will be:
View SolutionGravitational potential at a height R from the surface of the earth will be [Take M = mass of the earth, R = radius of the earth]
View Solution