Consider a ring of mass m and radius r. Maximum gravitational intensity on the axis of the ring has value.
Gmr2
2Gm√3r2
2Gm3√3r2
Gm2r2
The correct Answer is:C
To find the maximum gravitational intensity on the axis of a ring of mass m and radius r, we will follow these steps:
Step 1: Understand the Gravitational Intensity Formula
The gravitational intensity GP at a point P on the axis of the ring can be expressed as:
GP=Gmx(r2+x2)3/2
where:
- G is the gravitational constant,
- m is the mass of the ring,
- r is the radius of the ring,
- x is the distance from the center of the ring to the point P along the axis.
Step 2: Differentiate the Gravitational Intensity
To find the maximum gravitational intensity, we need to differentiate GP with respect to x and set the derivative equal to zero.
Using the quotient rule:
ddx(uv)=vdudx−udvdxv2
Let u=Gmx and v=(r2+x2)3/2.
Step 3: Apply the Quotient Rule
We find:
dudx=Gm
dvdx=32(r2+x2)1/2⋅2x=3x(r2+x2)1/2
Now, applying the quotient rule:
dGPdx=(r2+x2)3/2⋅Gm−Gmx⋅3x(r2+x2)1/2(r2+x2)3
Setting this equal to zero gives:
(r2+x2)3/2⋅Gm−Gmx⋅3x(r2+x2)1/2=0
Step 4: Simplify the Equation
This simplifies to:
Gm(r2+x2)3/2=3Gmx2(r2+x2)1/2
Dividing both sides by Gm(r2+x2)1/2 (assuming Gm≠0):
(r2+x2)=3x2
Rearranging gives:
r2=2x2
Thus, we find:
x=r√2
Step 5: Substitute Back to Find Maximum Gravitational Intensity
Now substitute x=r√2 back into the gravitational intensity formula:
GP=Gm(r√2)(r2+(r√2)2)3/2
Calculating r2+r22=3r22:
GP=Gm(r√2)(3r22)3/2=Gm(r√2)(3√38r3)=8Gm3√3r2
Final Result
Thus, the maximum gravitational intensity on the axis of the ring is:
GP=2Gm3√3r2
The gravitational intensity GP at a point P on the axis of the ring can be expressed as:
GP=Gmx(r2+x2)3/2
where:
- G is the gravitational constant,
- m is the mass of the ring,
- r is the radius of the ring,
- x is the distance from the center of the ring to the point P along the axis.
To find the maximum gravitational intensity, we need to differentiate GP with respect to x and set the derivative equal to zero.
ddx(uv)=vdudx−udvdxv2
Let u=Gmx and v=(r2+x2)3/2.
We find:
dudx=Gm
dvdx=32(r2+x2)1/2⋅2x=3x(r2+x2)1/2
Now, applying the quotient rule:
dGPdx=(r2+x2)3/2⋅Gm−Gmx⋅3x(r2+x2)1/2(r2+x2)3
Setting this equal to zero gives:
(r2+x2)3/2⋅Gm−Gmx⋅3x(r2+x2)1/2=0
This simplifies to:
Gm(r2+x2)3/2=3Gmx2(r2+x2)1/2
Dividing both sides by Gm(r2+x2)1/2 (assuming Gm≠0):
(r2+x2)=3x2
Rearranging gives:
r2=2x2
Thus, we find:
x=r√2
Now substitute x=r√2 back into the gravitational intensity formula:
GP=Gm(r√2)(r2+(r√2)2)3/2
Calculating r2+r22=3r22:
GP=Gm(r√2)(3r22)3/2=Gm(r√2)(3√38r3)=8Gm3√3r2
Thus, the maximum gravitational intensity on the axis of the ring is:
GP=2Gm3√3r2
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -C (Objective Type Questions (More than one option are correct))
12 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -D (Linked Comprehension Type Questions)
13 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -A (Objective Type Questions (one option is correct))
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
Mass of 1 kg is distributed uniformly over a ring of radius 1m. Find the gravitational potential at a point lies on the axis of the ring at a distance of 1m from the centre.
View SolutionMass of 20 kg is distributed uniformly over a ring of radius 2m. Find the the grvitational field at a point lies an th axis of the ring at a distance of 2√3 m from the centre.
View Solution
Knowledge Check
A thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring. The ring will now rotate with an angular velocity of
Aω(M−2m)(M+2m)BωM(M+2m)CωM(M+m)Dω(M+2m)M
A thin circular ring of mass m and radius R is rotating about its axis perpendicular to the plane of the ring with a constant angular velocity ω. Two point particleseach of mass M are attached gently to the opposite end of a diameter of the ring. The ring now rotates, with an angular velocityω2. Then the ratiomM is
View SolutionFor a uniform ring of mass M and radius R at its centre
View SolutionCalculate the moment of inertia of
a. a ring of mass M and radius R about an axis coinciding with the diameter of the ring.
b. as thin disc about an axis coinciding with the diameter.
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity omega. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be
View SolutionThe gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
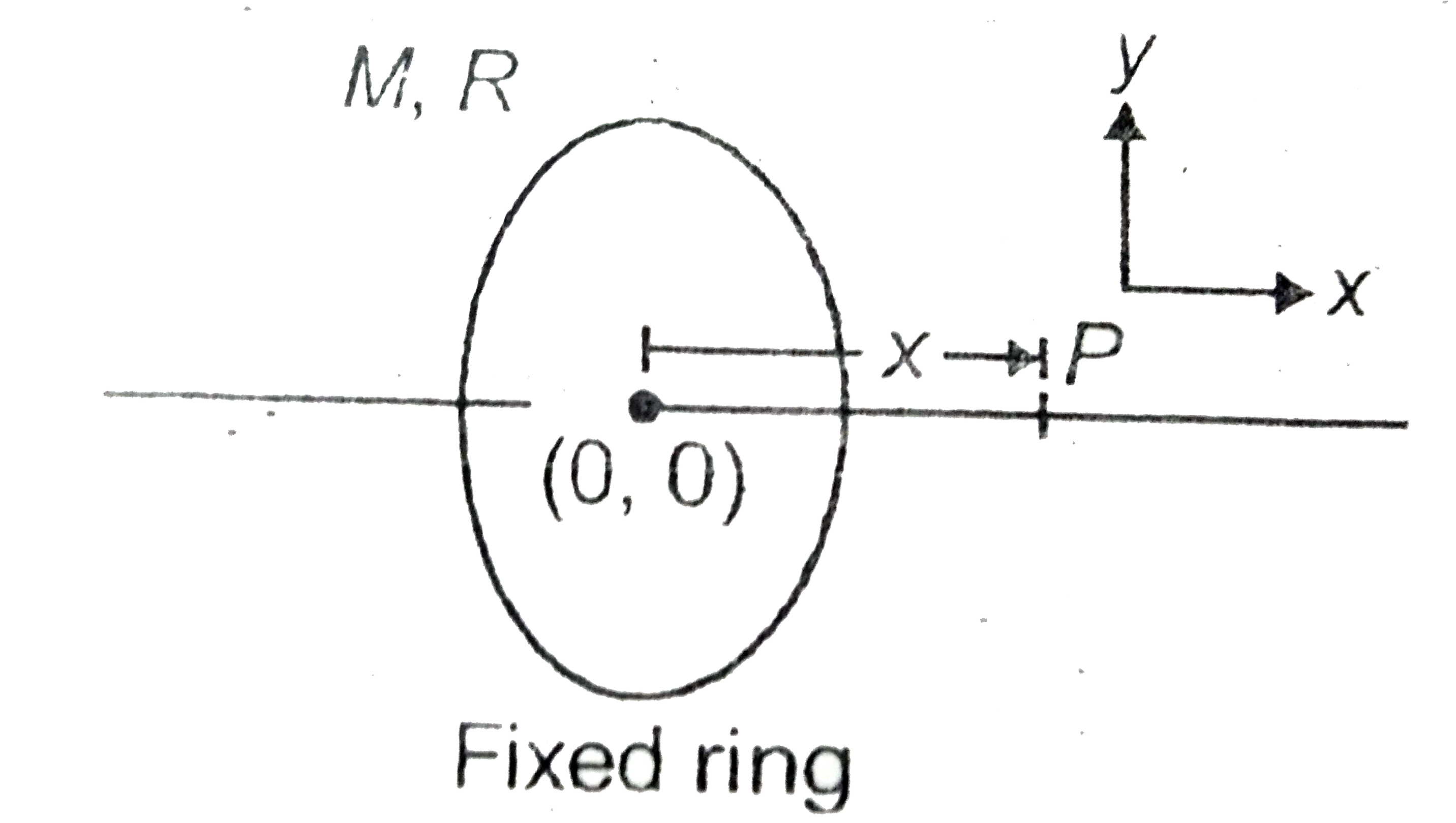
The value of maximum gravitational field intensity is
View SolutionThe M.I. of a ring of mass M and radius R about a tangential axis perpendicular to its plane is :
View Solution
