Match the items in column I to the items in column II given below Column-IColumn-II(A)Planet moving around the sun in the elliptical orbit(p)Linear momentum is conserved/constant(B)Planet moving around the sun in the fixed circular orbit(q)Angular momentum is conserved about one point in space.(C)A particle of mass m1 is projected towards a stationary mass m2. For m1 and m2 as system(r)Kinetic energy is conserved(D)A particle of mass m is projected by making an angle θ from the surface of the earth with speed less than escape velocity(s)Total energy is conserved
The correct Answer is:A, B, C, D
To match the items in Column I with those in Column II, we analyze each statement in Column I and determine the corresponding conservation laws or principles from Column II.
1. For Item A: "Planet moving around the sun in the elliptical orbit."
- In an elliptical orbit, the only force acting on the planet is the gravitational force from the sun, which is an internal force. Therefore:
- Total Energy is conserved (s).
- Angular Momentum is conserved about the sun (q).
- Linear Momentum is not conserved because the direction of the velocity changes, although the total momentum of the system remains constant.
- Kinetic Energy is not conserved in the strict sense because it varies at different points in the orbit.
- Matches: (A) → (s), (q).
2. For Item B: "Planet moving around the sun in the fixed circular orbit."
- In a circular orbit, the gravitational force provides the necessary centripetal force, and:
- Total Energy is conserved (s).
- Angular Momentum is conserved (q).
- Linear Momentum is conserved in magnitude but not direction.
- Kinetic Energy is conserved because the speed is constant.
- Matches: (B) → (s), (q), (r).
3. For Item C: "A particle of mass m1 is projected towards a stationary mass m2."
- In this case, since there are no external forces acting on the system of m1 and m2:
- Total Energy is conserved (s).
- Linear Momentum is conserved (p).
- Angular Momentum is conserved (q).
- Kinetic Energy is not conserved because some kinetic energy may be converted into other forms during the interaction (like heat or deformation).
- Matches: (C) → (s), (p), (q).
4. For Item D: "A particle of mass m is projected by making an angle theta from the surface of the earth with speed less than escape velocity."
- This is a projectile motion scenario:
- Total Energy is conserved (s).
- Linear Momentum is not conserved due to the gravitational force acting on the particle.
- Angular Momentum is conserved about the point of projection (q).
- Kinetic Energy is not conserved in the strict sense because it converts to potential energy at the peak.
- Matches: (D) → (s), (q).
Final Matches:
- (A) → (s), (q)
- (B) → (s), (q), (r)
- (C) → (s), (p), (q)
- (D) → (s), (q)
- In an elliptical orbit, the only force acting on the planet is the gravitational force from the sun, which is an internal force. Therefore:
- Total Energy is conserved (s).
- Angular Momentum is conserved about the sun (q).
- Linear Momentum is not conserved because the direction of the velocity changes, although the total momentum of the system remains constant.
- Kinetic Energy is not conserved in the strict sense because it varies at different points in the orbit.
- Matches: (A) → (s), (q).
- In a circular orbit, the gravitational force provides the necessary centripetal force, and:
- Total Energy is conserved (s).
- Angular Momentum is conserved (q).
- Linear Momentum is conserved in magnitude but not direction.
- Kinetic Energy is conserved because the speed is constant.
- Matches: (B) → (s), (q), (r).
- In this case, since there are no external forces acting on the system of m1 and m2:
- Total Energy is conserved (s).
- Linear Momentum is conserved (p).
- Angular Momentum is conserved (q).
- Kinetic Energy is not conserved because some kinetic energy may be converted into other forms during the interaction (like heat or deformation).
- Matches: (C) → (s), (p), (q).
- This is a projectile motion scenario:
- Total Energy is conserved (s).
- Linear Momentum is not conserved due to the gravitational force acting on the particle.
- Angular Momentum is conserved about the point of projection (q).
- Kinetic Energy is not conserved in the strict sense because it converts to potential energy at the peak.
- Matches: (D) → (s), (q).
- (A) → (s), (q)
- (B) → (s), (q), (r)
- (C) → (s), (p), (q)
- (D) → (s), (q)
Topper's Solved these Questions
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:ASSIGNMENT SECTION -G (Integer Answer Type Questions)
Explore 6 Videos
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:ASSIGNMENT SECTION -H (Multiple True - False Type Questions)
Explore 5 Videos
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:ASSIGNMENT SECTION -E (Assertion - Reason Type Questions)
Explore 14 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - D
Explore 9 Videos
- KINETIC THEORYBook:AAKASH INSTITUTE ENGLISHChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
Similar Questions
Match the items in column I with those given in column II.
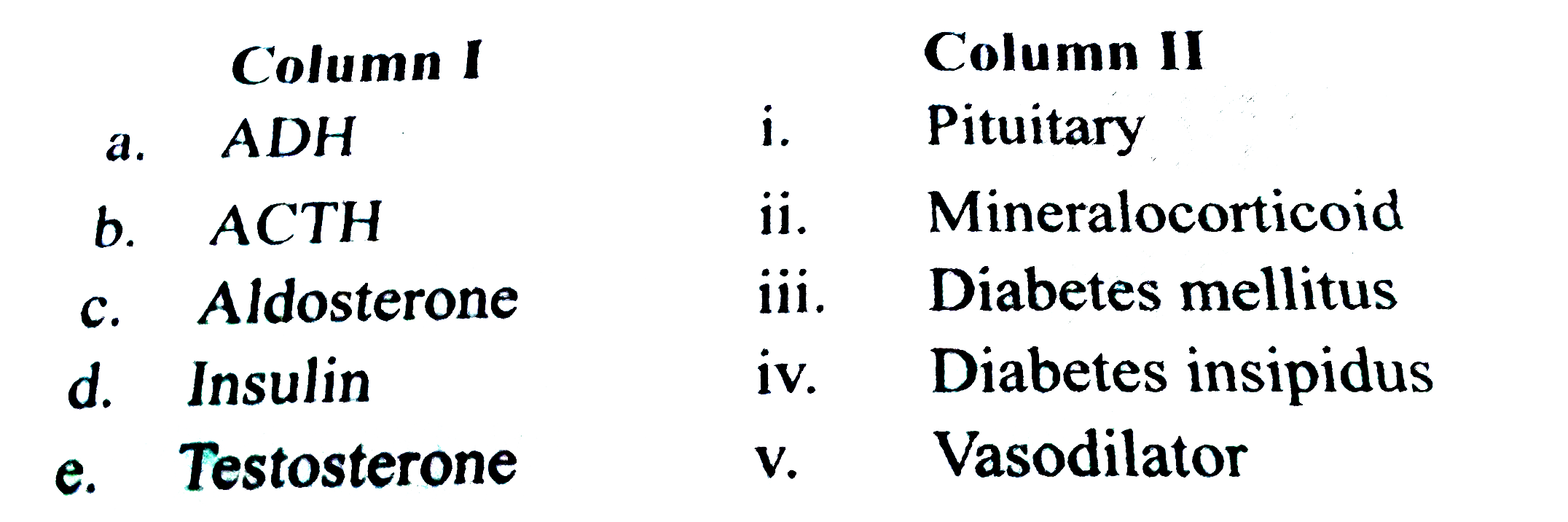
View SolutionMatch the items in column I with relevant items in column II

View SolutionMatch the items in Column I with those in Column II
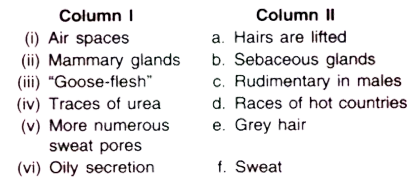
View SolutionMatch the items of Column I with items of Column II.

View SolutionMatch the items of Column I with items of Column II.

View SolutionMatch the items in the column I with those in the column II.

View SolutionMatch the items in Column I with the relevant item in column II.
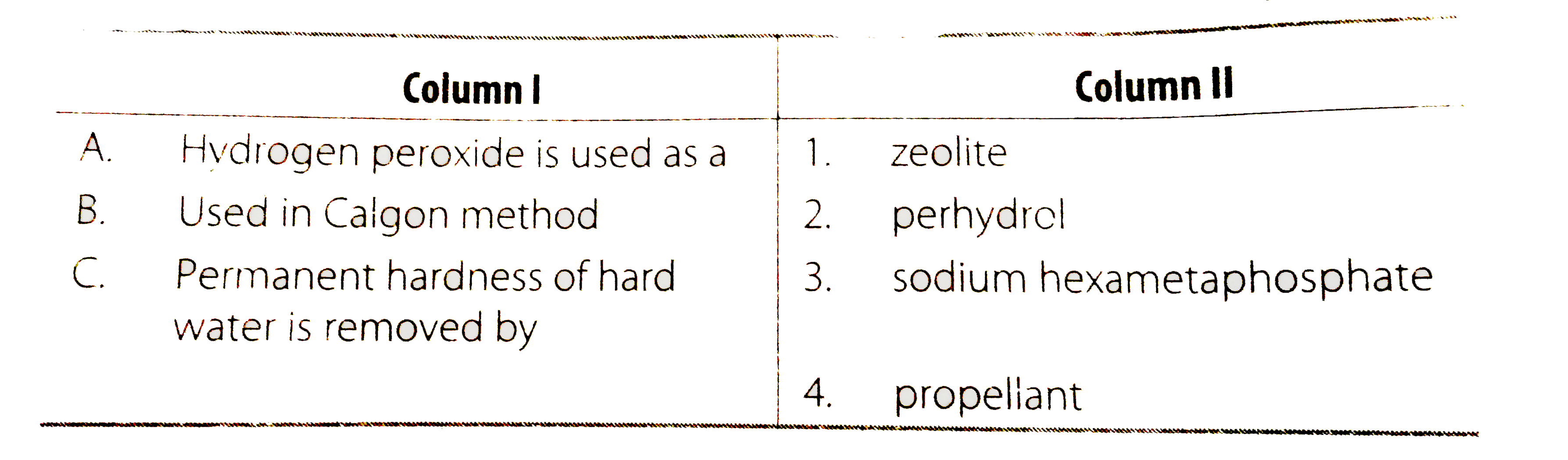
View SolutionMatch the item of columns I and II

View Solutionmatch the items given in column I with the items given in column II.
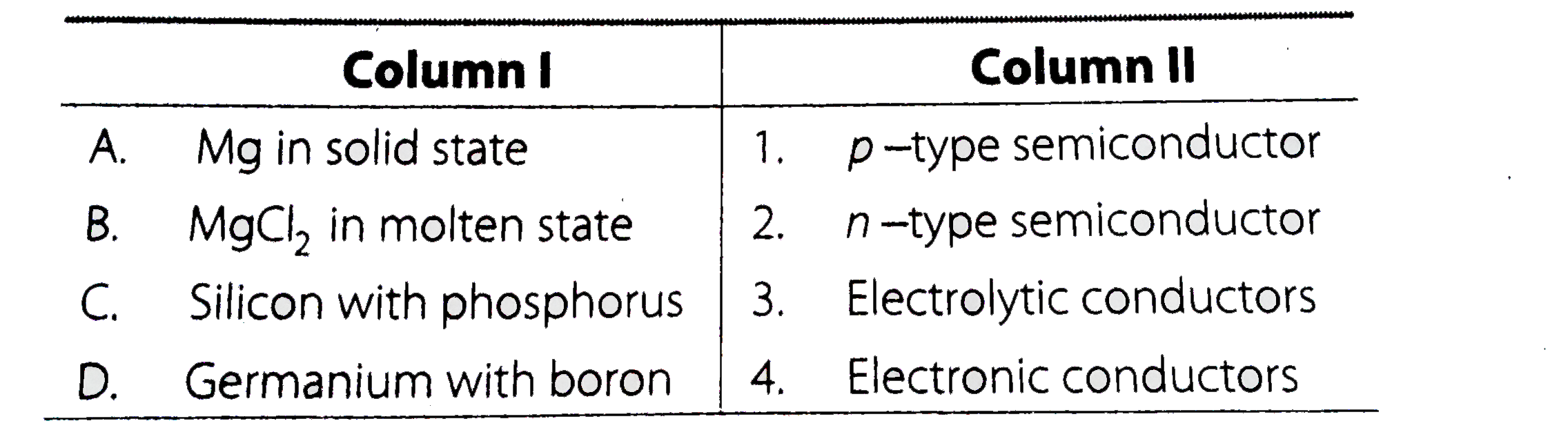
View Solutionmatch the items given in column I with the items given in column II.
View Solution