A planet moves in elliptical around sun, at one of focal points. Match the following, for different parameters related to the planet during the motion
Column IColumn II(A)Kinetic energy(p)Maximum at perigee(B)Gravitational potential energy(q)Minimum at perigee(C)Linear momentum(r)Maximum at apogee(D)Area swept per second radius(s)Minimum at apogee
The correct Answer is:A, B, C, D
To solve the problem, we need to analyze the parameters related to a planet moving in an elliptical orbit around the Sun. The parameters we need to match are Kinetic Energy, Gravitational Potential Energy, Linear Momentum, and Area Swept per Second Radius.
1. Understanding the Orbit:
- The planet moves in an elliptical orbit with the Sun at one of the foci. The closest point to the Sun is called the perigee, and the farthest point is called the apogee.
2. Kinetic Energy (KE):
- Kinetic Energy is given by the formula KE=12mv2.
- At perigee, the planet is closest to the Sun and moves at its highest speed, thus the kinetic energy is maximum at perigee.
- At apogee, the planet is farthest from the Sun and moves at its lowest speed, thus the kinetic energy is minimum at apogee.
- Conclusion: Kinetic Energy is maximum at perigee (p) and minimum at apogee (q).
3. Gravitational Potential Energy (GPE):
- Gravitational Potential Energy is given by GPE=−GMmr.
- At perigee, the distance r is minimum, which means the potential energy is at its most negative value (minimum).
- At apogee, the distance r is maximum, which means the potential energy is less negative (maximum).
- Conclusion: Gravitational Potential Energy is minimum at perigee (q) and maximum at apogee (p).
4. Linear Momentum (p):
- Linear Momentum is defined as p=mv.
- Since velocity is maximum at perigee and minimum at apogee, linear momentum will also be maximum at perigee and minimum at apogee.
- Conclusion: Linear Momentum is maximum at perigee (p) and minimum at apogee (r).
5. Area Swept per Second Radius:
- According to Kepler's second law, the area swept out by the radius vector in a given time is constant.
- The area swept per unit time is constant, but the radius r changes. As the radius increases (at apogee), the area swept per second radius decreases.
- Conclusion: Area swept per second radius is maximum at perigee (s) and minimum at apogee (D).
Final Matching:
- A: Kinetic Energy → Maximum at perigee (p)
- B: Gravitational Potential Energy → Minimum at perigee (q)
- C: Linear Momentum → Maximum at perigee (r)
- D: Area swept per second radius → Minimum at apogee (s)
Summary of Answers:
- A → p
- B → q
- C → r
- D → s
- The planet moves in an elliptical orbit with the Sun at one of the foci. The closest point to the Sun is called the perigee, and the farthest point is called the apogee.
- Kinetic Energy is given by the formula KE=12mv2.
- At perigee, the planet is closest to the Sun and moves at its highest speed, thus the kinetic energy is maximum at perigee.
- At apogee, the planet is farthest from the Sun and moves at its lowest speed, thus the kinetic energy is minimum at apogee.
- Conclusion: Kinetic Energy is maximum at perigee (p) and minimum at apogee (q).
- Gravitational Potential Energy is given by GPE=−GMmr.
- At perigee, the distance r is minimum, which means the potential energy is at its most negative value (minimum).
- At apogee, the distance r is maximum, which means the potential energy is less negative (maximum).
- Conclusion: Gravitational Potential Energy is minimum at perigee (q) and maximum at apogee (p).
- Linear Momentum is defined as p=mv.
- Since velocity is maximum at perigee and minimum at apogee, linear momentum will also be maximum at perigee and minimum at apogee.
- Conclusion: Linear Momentum is maximum at perigee (p) and minimum at apogee (r).
- According to Kepler's second law, the area swept out by the radius vector in a given time is constant.
- The area swept per unit time is constant, but the radius r changes. As the radius increases (at apogee), the area swept per second radius decreases.
- Conclusion: Area swept per second radius is maximum at perigee (s) and minimum at apogee (D).
- A: Kinetic Energy → Maximum at perigee (p)
- B: Gravitational Potential Energy → Minimum at perigee (q)
- C: Linear Momentum → Maximum at perigee (r)
- D: Area swept per second radius → Minimum at apogee (s)
- A → p
- B → q
- C → r
- D → s
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -G (Integer Answer Type Questions)
6 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -H (Multiple True - False Type Questions)
5 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -E (Assertion - Reason Type Questions)
14 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
Match the following columns. (for a satellite in circular orbit)
Column-IColumn-II(A)Kinetic energy(p)−GMm2r(B)Potential energy(q)√GMr(C)Total energy(r)−GMmr(D)Orbital speed(s)GMm2r
View SolutionMatch the following :
Column -IColumn -II(A)Acceleration due to gravity(p)Kepler's law(B)Law of periods(q)Vector quantity(C)Orbital speed(r)Uniform near earth surface(D)Gravitational potential(s)Is nearly zero at infinity
View SolutionDensity of a planet is two times the density of earth. Radius of this planet is half. Match the following (as compared to earth)
Column-IColumn-II(A)Accleration due to gravity on this planet's surface(p)Half(B)Gravitational potential on the surface(q)Same(C)Gravitational potential at centre(r)Two times(D)Gravitational field strength at centre(s)Four times
View SolutionMatch the following
Column-IColumn-II(A)Enthalpy(p)Extensive property(B)Entropy(q)H - TS(C)Free energy(r)E + PV(D)Pressure(s)Intensive property
View SolutionIn elliptical orbit of a planet, as the planet moves from apogee position to perigee position to perigee position, match the following columns
Column-IColumn-II(A)Speed of planet(p)Remains same(B)Distance of planet from centre of sun(q)Decreases(C)Potential energy(r)Increase(D)Angular momentum about centre of sun(s)Cannot say
View SolutionIf earth decreases its rotational speed. Match the following columns
Column-IColumn-II(A)Value of g at pole(p)Will remain same(B)Value of g at equator(q)Will increase(C)Distance of geostationary(r)Will decrease(D)Energy of geostationary satellite(s)Cannot say
View SolutionIf some charge is given to a conducting object of any shape, then match the following columns, under electrostatic condition
Column IColumn II(A)→E at a point within conducting material(p)Must be zero(B)→Eat a point outside the material (q)May be Zero(C)→Eat a point in a cavity having no charge(r)May be uniform but not zero(D)→Eat a point in the cavity having some charge(s)May be non-uniform(t)Cannot predict
View SolutionTwo concentric spherical shells are as shown in figure. Match the following columns
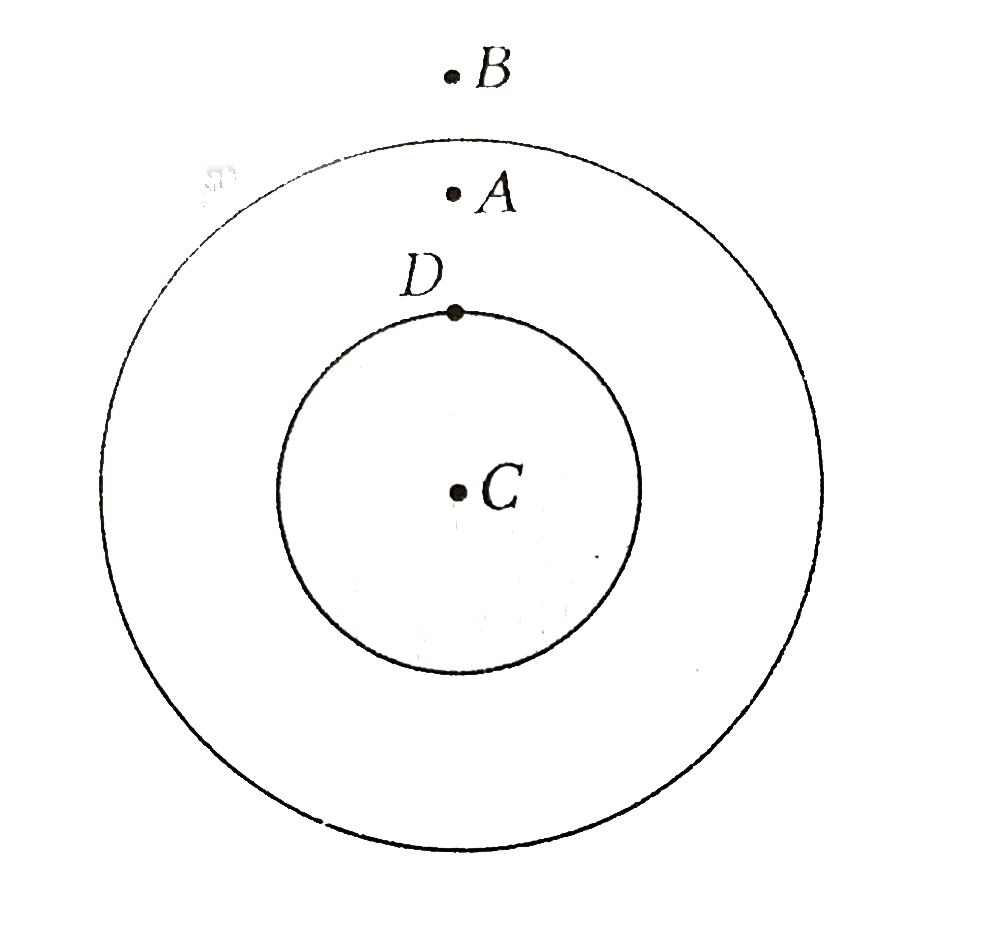
Column-IColumn-II(A)Potential at A(p)greater than B(B)Gravitational field at A(q)less than B(C)As one moves from C to D(r)Potential remains constant(D)As one moves from D to A(s)Gravitational field decreases(t)None
View SolutionA solid sphere is rotating about an axis shown in figure. An insect follows the dotted path on the circumference of sphere as shown in the figure.
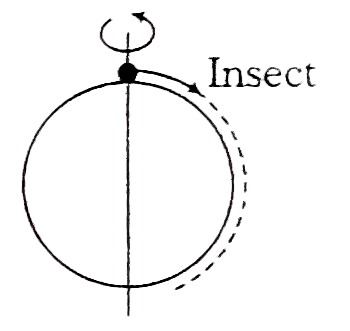
Column-IColumn-II(A)Moment of inertia(p)Will remain constant(B)Angular velocity(q)Will first increase, then decrease(C)Angular momentum(r)Will first decrease then increase(D)Rotational kinetic energy(s)Will continuously decrease(t)Will continuously increase
View SolutionMatch the following :
{:(,"Column-I",,"Column-II"),((A),"Velocity",(p),"Increased,"n uarr z darr),((B), "Potential Energy",(q),"Increased,"ndarrzuarr),((C ),E_(n)-E_(n-1) (E="Total energy for H atom "(n cancel(=)1)),(r ),"Decreased,"n uarr ),((D),"Separation energy (For H atom)",(s),"No change"n uarr):}
View Solution