A body is suspended on a spring balance in a ship sailing along the equator with a speed v. Show that the scale reading will be very close to W0(1±2ωvg), where ω is the angular speed of the earth and W0 is the reading of spring balance when the ship is at rest. Explain the plus or minus sign
To solve the problem, we need to analyze the forces acting on a body suspended in a spring balance on a ship sailing along the equator with a speed v. We will derive the expression for the scale reading when the ship is in motion.
Step 1: Understanding the Forces at Rest
When the ship is at rest, the reading on the spring balance, denoted as W0, is equal to the weight of the body. The effective gravitational force acting on the body is given by:
W0=mgeffective=mg−mω2R
where g is the acceleration due to gravity, ω is the angular speed of the Earth, and R is the radius of the Earth.
Step 2: Considering the Motion of the Ship
When the ship is moving with speed v, we need to consider the effective gravitational force acting on the body. The centripetal acceleration due to the Earth's rotation and the ship's motion will affect the reading on the spring balance.
Step 3: Analyzing the Two Cases
1. Case 1: The ship is moving in the same direction as the Earth's rotation (i.e., v is in the direction of ωR).
2. Case 2: The ship is moving in the opposite direction to the Earth's rotation (i.e., v is opposite to ωR).
In both cases, we will derive the effective weight W′ when the ship is moving.
Step 4: Deriving the Expression for W′
Using the centripetal force concept, the effective weight when the ship is moving can be expressed as:
W′=mg−m((v±ωR)2R)
This simplifies to:
W′=mg−m(v2±2vωR+ω2R2R)
Step 5: Simplifying the Expression
We can neglect the terms v2 and ω2R2 as they are much smaller compared to the other terms. Thus, we have:
W′≈mg−m(2vω)
Factoring out mg, we get:
W′≈mg(1−2vωg)
Step 6: Final Expression
Therefore, the reading on the spring balance when the ship is moving is:
W′≈W0(1±2ωvg)
where W0 is the reading when the ship is at rest.
Explanation of the Plus/Minus Sign
- The plus sign occurs when the ship is moving in the opposite direction to the rotation of the Earth, effectively increasing the apparent weight.
- The minus sign occurs when the ship is moving in the same direction as the rotation of the Earth, effectively decreasing the apparent weight.
When the ship is at rest, the reading on the spring balance, denoted as W0, is equal to the weight of the body. The effective gravitational force acting on the body is given by:
W0=mgeffective=mg−mω2R
where g is the acceleration due to gravity, ω is the angular speed of the Earth, and R is the radius of the Earth.
When the ship is moving with speed v, we need to consider the effective gravitational force acting on the body. The centripetal acceleration due to the Earth's rotation and the ship's motion will affect the reading on the spring balance.
1. Case 1: The ship is moving in the same direction as the Earth's rotation (i.e., v is in the direction of ωR).
2. Case 2: The ship is moving in the opposite direction to the Earth's rotation (i.e., v is opposite to ωR).
Using the centripetal force concept, the effective weight when the ship is moving can be expressed as:
W′=mg−m((v±ωR)2R)
This simplifies to:
W′=mg−m(v2±2vωR+ω2R2R)
We can neglect the terms v2 and ω2R2 as they are much smaller compared to the other terms. Thus, we have:
W′≈mg−m(2vω)
Factoring out mg, we get:
W′≈mg(1−2vωg)
Therefore, the reading on the spring balance when the ship is moving is:
W′≈W0(1±2ωvg)
where W0 is the reading when the ship is at rest.
- The plus sign occurs when the ship is moving in the opposite direction to the rotation of the Earth, effectively increasing the apparent weight.
- The minus sign occurs when the ship is moving in the same direction as the rotation of the Earth, effectively decreasing the apparent weight.
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - TRY YOUR SELF
33 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - EXERCISE
17 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -I (Subjective Type Question)
9 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
A body suspended on a spring balance in a ship weighs W0 when the ship is at rest. When the ship begins to move along the equator with a speed v, show that the scale reading is very close to W0(1±2ωV/g), where ω is the angular speed of the earth.
View SolutionA body is suspended from a spring balance kept in a satellite. The reading of the balance is W1 when the satellite goes in an orbit of radius R and is W2 when it goes in an orbit of radius 2R.
View SolutionFind the average speed of a particle whose velocity is given by V=V0sinωt t where T=2π/ω is the time of complete cycle
View Solution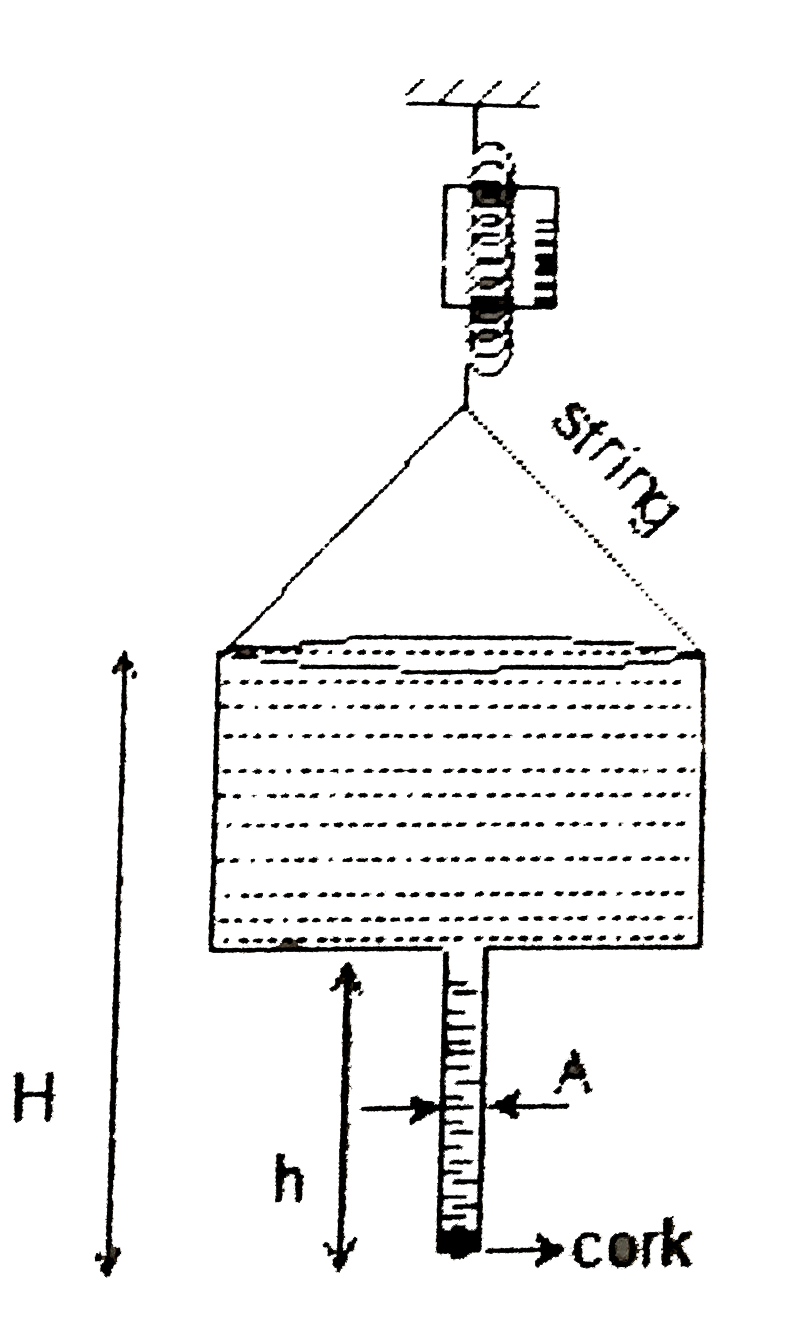
A vessel completely filled wit water is suspended with help of strings from a spring balance as shwon in figure. A cork is plugged at the bottom of the vessel. If the initial reading of the spring balannce is W0. Then the reading of the spring balance just after the cork is removed and the liquid begins to flow out will be [ρ= density of liquid & A=coss -sectional area of narrow pipe]
View SolutionA pendulum having a bob of mas m is hanging in a ship sailing along the equator from east to west. When the ship is stationary with respect to water the tension in the string is T0. a. Find the speed of the ship due to rotation of the earth about its axis. b. find the difference between T0 and the earth's attraction on the bob. c. If the ship sails at speed v, what is the tension in the string ? Angular speed of earth's rotation is ω and radius of the earth is R.
View SolutionA satellite moves estwards very near the surface of the Earth in equitorial plane with speed (v0). Another satellite moves at the same height with the same speed in the equatorial plane but westwards. If R =radius of the Earth and ω be its angular speed of the Earth about its own axis. Then find the approximate difference in the two time period as observed on the earth.
View SolutionA spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this spring, when displaced and released, oscillates with a period of 0.6s. What is the weight of the body? When 50 kg is put, the extension of spring is 20 cm.
View SolutionWeight of a body depends directly upon acceleration due to gravity g. Value of g depends upon many factors. It depends upon the shape of earth, rotation earth etc. Weight of a body at a pole is more then that at a place on equator because g is maximum at poles and minimum on equator. Acceleration due to gravity g varies with latitude λ as per relation given below :
grot=g−Rω2cos2λ where R is radius of earth and ω is angular velocity of earth. A body of mass m weighs Wr in a train at rest. The train then begins to run with a velocity v around the equator from west to east. It observed that weight Wm of the same body in the moving train is different from Wr. Let vebe the velocity of a point on equator with respect to axis of rotation of earth and R be the radius of the earth. Clearly the relative between earth and trainwill affect the weight of the body.
Difference between Weight Wr and the gravitational attraction on the body can be given as
View SolutionWeight of a body depends directly upon acceleration due to gravity g. Value of g depends upon many factors. It depends upon the shape of earth, rotation earth etc. Weight of a body at a pole is more then that at a place on equator because g is maximum at poles and minimum on equator. Acceleration due to gravity g varies with latitude λ as per relation given below :
grot=g−Rω2cos2λ where R is radius of earth and ω is angular velocity of earth. A body of mass m weighs Wr in a train at rest. The train then begins to run with a velocity v around the equator from west to east. It observed that weight Wm of the same body in the moving train is different from Wr. Let vebe the velocity of a point on equator with respect to axis of rotation of earth and R be the radius of the earth. Clearly the relative between earth and trainwill affect the weight of the body.
Weight Wm of the body can be given as
View SolutionA rocket starts vertically upward with speed v0. Show that its speed v at height h is given by v20−v2=2hg1+hR
where R is the radius of the earth and g is acceleration due to gravity at earth's suface. Deduce an expression for maximum height reachhed by a rocket fired with speed 0.9 times the escape velocity.
View Solution