A metal block of area 0.10 m2 placed at a table, is connected to a 0.010 kg mass via a string that passes over an ideal pulley. Th pulley is fixed at the edge of the table. A liquid with a film of thickness 0.30 mm is placed between the block and the table. If the coefficient of viscosity of the liquid is 3.45×10−3 Pa s, with what constant velocity does the block move when released?
To solve the problem step by step, we will follow these calculations:
Step 1: Understand the forces acting on the block
When the metal block is released, it will experience two main forces:
- The gravitational force acting downwards due to the mass connected to it.
- The viscous force acting upwards due to the liquid film between the block and the table.
Step 2: Calculate the gravitational force (Weight)
The weight (W) of the mass connected to the block can be calculated using the formula:
W=mg
Where:
- m=0.010kg (mass)
- g=9.81m/s2 (acceleration due to gravity)
Calculating the weight:
W=0.010kg×9.81m/s2=0.0981N
Step 3: Set up the equation for viscous force
The viscous force (F) acting on the block can be expressed using the formula for viscous drag:
F=ηAVy
Where:
- η=3.45×10−3Pa s (coefficient of viscosity)
- A=0.10m2 (area of the block)
- V is the constant velocity we want to find
- y=0.30mm=0.30×10−3m (thickness of the liquid film)
Step 4: Equate the gravitational force to the viscous force
At constant velocity, the gravitational force will equal the viscous force:
W=F
Substituting the expressions we have:
0.0981N=ηAVy
Step 5: Substitute the known values into the equation
Substituting the values we have:
0.0981=(3.45×10−3)(0.10)V(0.30×10−3)
Step 6: Simplify the equation
Rearranging gives:
0.0981=(3.45×10−3)0.10V0.30×10−3
0.0981=(3.45×10−3)×0.100.30×10−3V
0.0981=(3.45×0.100.30)V
Calculating the constant:
0.100.30=13
Thus:
0.0981=(3.45×13)V
0.0981=1.15×10−3V
Step 7: Solve for V
Now, solving for V:
V=0.09811.15×10−3
V≈85.65m/s
Final Answer
The constant velocity at which the block moves when released is approximately:
V≈0.0857m/s
When the metal block is released, it will experience two main forces:
- The gravitational force acting downwards due to the mass connected to it.
- The viscous force acting upwards due to the liquid film between the block and the table.
The weight (W) of the mass connected to the block can be calculated using the formula:
W=mg
Where:
- m=0.010kg (mass)
- g=9.81m/s2 (acceleration due to gravity)
W=0.010kg×9.81m/s2=0.0981N
The viscous force (F) acting on the block can be expressed using the formula for viscous drag:
F=ηAVy
Where:
- η=3.45×10−3Pa s (coefficient of viscosity)
- A=0.10m2 (area of the block)
- V is the constant velocity we want to find
- y=0.30mm=0.30×10−3m (thickness of the liquid film)
At constant velocity, the gravitational force will equal the viscous force:
W=F
Substituting the expressions we have:
0.0981N=ηAVy
Substituting the values we have:
0.0981=(3.45×10−3)(0.10)V(0.30×10−3)
Rearranging gives:
0.0981=(3.45×10−3)0.10V0.30×10−3
0.0981=(3.45×10−3)×0.100.30×10−3V
0.0981=(3.45×0.100.30)V
0.100.30=13
Thus:
0.0981=(3.45×13)V
0.0981=1.15×10−3V
Now, solving for V:
V=0.09811.15×10−3
V≈85.65m/s
The constant velocity at which the block moves when released is approximately:
V≈0.0857m/s
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - A50videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - B23videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J9videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)26videos
MAGNETISM AND MATTER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)14videos
MECHANICAL PROPERTIES OF SOLIDS
Similar Questions
A metal block of area 0.10 m2 is connected to a 0.02 kg mass via a string. The string passes over an ideal pulley (considered massless and frictionless) as shown in figure. A liquid with a flim of thickness 0.15 mm is placed between the plate and the table. When released the plate movees to the right with a constant speed of 0.075 m s−1. What is the coefficient of viscosity of the liquid?
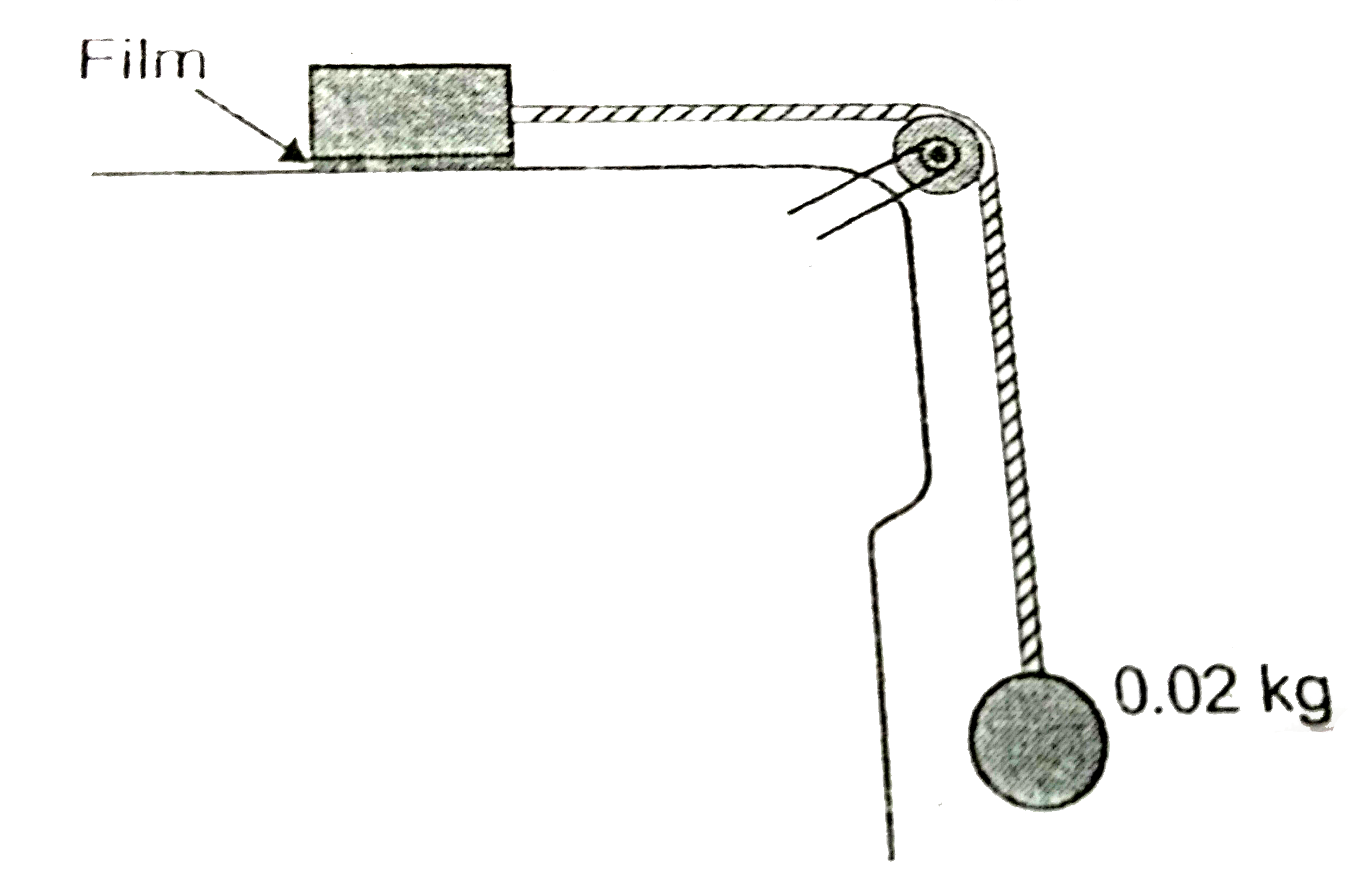 View Solution
View SolutionA metal plate of area 0.10m2 is connected to a 0.01kg mass via a string that passes over an ideal pulley (considered to be friction-less), as shown in the figure. A liquid with a film thickness of 3.0mm is placed between the plate and the table. When released the plate moves to the right with a constant speed of 0.085ms−1. Find the coefficient of viscosity of the liquid.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A metal block of area 0.10m2 is connected to a 0.01 kg mass via a string that passes over a massless and frictionless pulley as shoen in figure.A liquid with a film thickness of 0.3 mm is placed between the block and the table. When released the block moves to the right with a constant of 0.085ms−1. The cofficient of viscosity of the liquid is
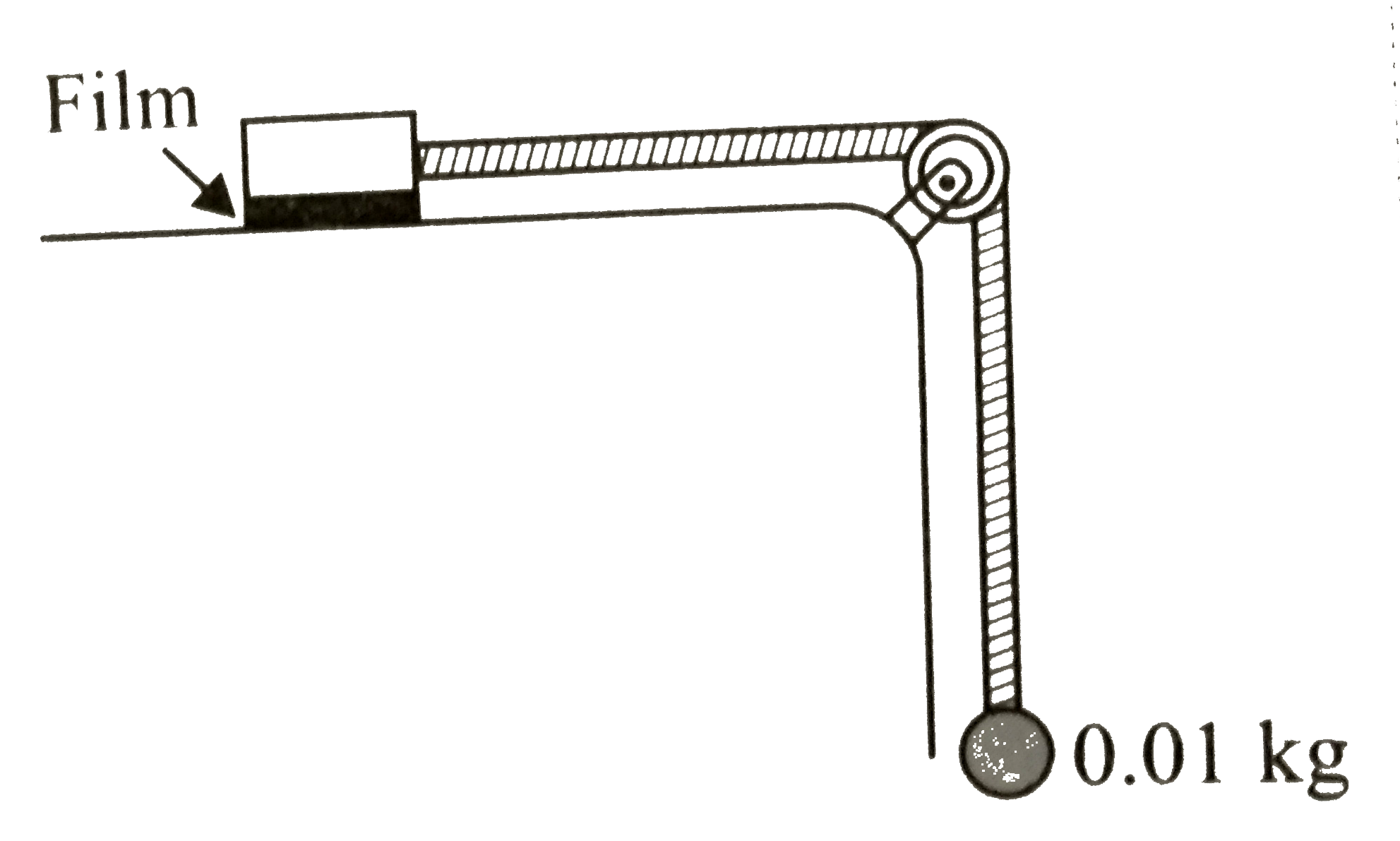 A2.5×10−3Pa sB3.5×10−3 Pa sC4.5×10−3 Pa sD6.5×10−3 Pa s
A2.5×10−3Pa sB3.5×10−3 Pa sC4.5×10−3 Pa sD6.5×10−3 Pa s - Question 2 - Select One
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A metal plate of area 0.10m2 is connected to a 0.04kg mass via a string that passes over an ideal pulley (considered massless and frictionless) A liquid with a film of thickness of 0.3mm is placed between the plate and the table. When system is released, the plate moves up with constant speed of 0.085m/s. Find the approximate value of coefficient of viscosity of the liquid. (mass of metal plate is 0.02kg, g=9.8m/s2)
 View Solution
View SolutionA block of mass M is placed on a horizontal surface. It is tied with an inextensible string that passes through ideal pulleys. A mass m is connected to the pulley as shown. For what value of m, the block M will accelerate towards the fixed pulley ?
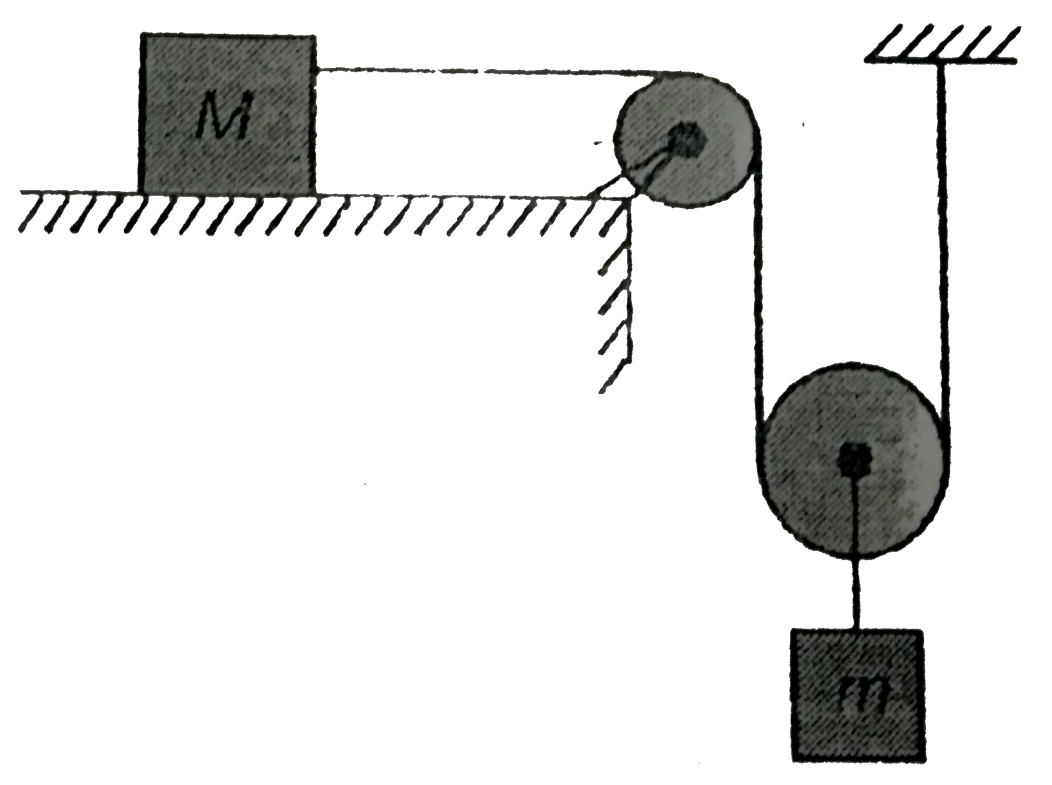 View Solution
View SolutionA body of mass 20 kg is resting on a table. A light string is attached to it and passed over a smooth pulley at the edge of the table and a mass 3kg is attached at the free end. What is the acceleration of the system of the coefficient of kinetic friction between the mass and the table is 0.04 ? What is the tension in the string ?
View SolutionA block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View SolutionThree blocks of masses 3 kg, 6 kg and 1 kg are connected by a string passing over two smooth pulleys attached at the two ends of the horizontal surface. If the co-efficient of friction between the block and the surface is 0.6, the frictional force acting on the block of mass 6 kg is
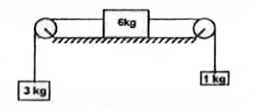 View Solution
View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly
 View Solution
View Solution

