To what height does the liquid rise in a capillary tube of radus 0.25 mm, when dipped in a liquid of density 0.8×103kgm−3 and surface tension 0.05 N m−1? Given (cosθ=0.4)
To find the height to which the liquid rises in a capillary tube, we can use the formula for capillary rise:
h=2⋅γ⋅cosθρ⋅g⋅r
where:
- h = height of the liquid column
- γ = surface tension of the liquid
- θ = angle of contact
- ρ = density of the liquid
- g = acceleration due to gravity
- r = radius of the capillary tube
Step 1: Identify the given values
- Radius of the capillary tube, r=0.25mm=0.25×10−3m
- Density of the liquid, ρ=0.8×103kg/m3
- Surface tension, γ=0.05N/m
- Cosine of the angle of contact, cosθ=0.4
- Acceleration due to gravity, g=10m/s2
Step 2: Substitute the values into the formula
Now we can substitute these values into the formula for h:
h=2⋅0.05⋅0.40.8×103⋅10⋅0.25×10−3
Step 3: Calculate the numerator
Calculate the numerator:
2⋅0.05⋅0.4=0.04
Step 4: Calculate the denominator
Calculate the denominator:
0.8×103⋅10⋅0.25×10−3=0.8⋅103⋅10⋅0.25⋅10−3=0.8⋅10⋅0.25=2
Step 5: Calculate the height h
Now substitute the values back into the equation:
h=0.042=0.02m
Step 6: Convert to millimeters
To convert meters to millimeters:
h=0.02m=20mm
Final Answer
The height to which the liquid rises in the capillary tube is h=20mm.
---
- h = height of the liquid column
- γ = surface tension of the liquid
- θ = angle of contact
- ρ = density of the liquid
- g = acceleration due to gravity
- r = radius of the capillary tube
- Radius of the capillary tube, r=0.25mm=0.25×10−3m
- Density of the liquid, ρ=0.8×103kg/m3
- Surface tension, γ=0.05N/m
- Cosine of the angle of contact, cosθ=0.4
- Acceleration due to gravity, g=10m/s2
Now we can substitute these values into the formula for h:
Calculate the numerator:
Calculate the denominator:
Now substitute the values back into the equation:
To convert meters to millimeters:
The height to which the liquid rises in the capillary tube is h=20mm.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - A
50 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - B
23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
Find the total pressure inside a sperical air bubble of radius 0.2 mm. The bubble is at a depth 5 cm below the surface of a liquid of density 2×103 kg m−3 and surface tension 0.082 N m−1. (Given : atmospheric pressure = 1.01 ×105Nm−2)
Hint : Pi=Po+2SR
Po = atmospheric pressure + gauge pressure of liquid column.
View SolutionTo what height does a liquid of density 0.4×103 kg m−3 and surface tension 0.05 Nm−1 rise in a capillary tube of radius 0.2 mm when dipped in ? [Given cosθ=0.4g=10ms−2]
View Solution
Knowledge Check
The rise in the water level in a capillary tube of radius 0.07 cm when dipped veryically in a beaker containing water of surface tension 0.07Nm−1 is (g = 10ms−2)
A2 cmB4 cmC1.5 cmD3 cmTwo capillary tubes of radii 0.2 cm and 0.4 cm are dipped in the same liquid.The ratio of heights through which liquid will rise in the tube is
A1:2B2:1C1:4D4:1
With what terminal velocity will an air bubble of radius 0.2 mm. rise in a liquid of viscosity 0.15Nsm−2 and specific gravity 0.9 ? Density of air1.3kgm−3
View SolutionA barometer contains two uniform capillries of radii 1.44×10−3m and 7.2×10−4m. If the height of the liquid in the narrow tube is 0.2m more than that in the wide tube, calculate the true pressure difference. Density of liquid =103kg/m3, surface tension =72×10−3N/m and g=m/s2.
View SolutionChoose the correct option:
A capillary tube of radius r is lowered into a liquid of surface tension T and density ρ. Given angle of contact =0∘.
The work done by surface tension will be
View SolutionCalculate the height to which water will rise in a capillary tube of diameter 1×10−3m [given surface tension of water is 0.072Nm−1 angle of contact is 0∘,g=9.8ms−2 and density of water =1000kgm−3]
View SolutionCalculate the pressure indise a small air bubble of radius 0.01mm situated at a depth of h=20m below the fre surface of liquid of density ρ1=103kg/m3,ρ2=800km/m3 and surface tension T2=7.5×10−2N/m. The thickness of the first liqid is h1=15m and h2=25m.
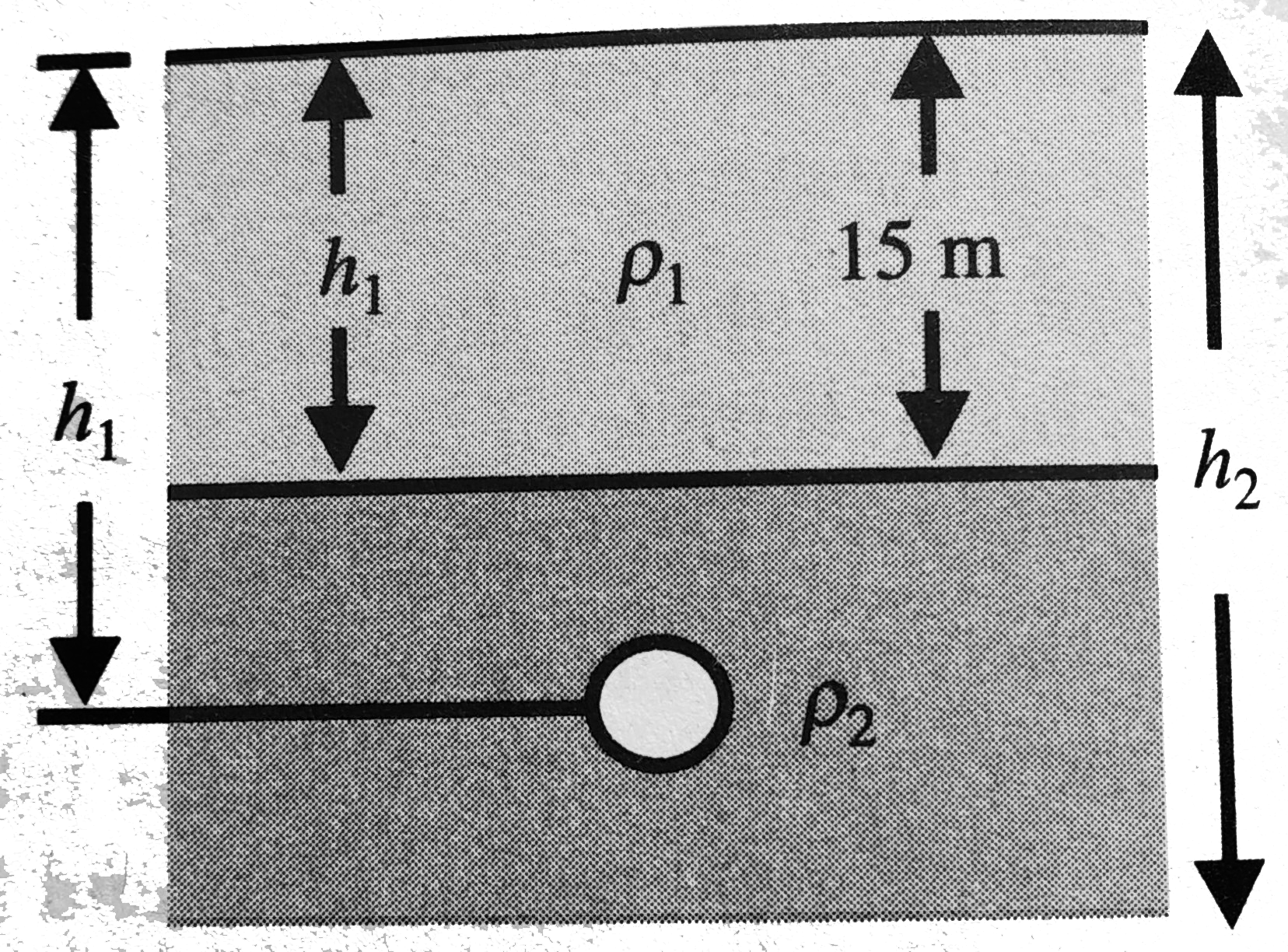
View SolutionA barometer contains two uniform capillaries of radii 1.4×10−3m and 7.2×10−4m. If the height of liquid in narrow tube is 0.2m more than that in wide tube, calculate the true pressure difference. Density of liquid =103kg/m3, surface tension =72×10−3N/m and g=9.8ms−12.
View Solution
