A wooden cylinder of length l floats vertically in a liquid of specific gravity ρ with (13)rd part of its length submerged. Another liquid that is immiscible with the previous liquid is poured into it, to just completely submerge the cylinder. If the density of the liquid at the bottom, density of cylinder and density of upper liquid are in G.P., find the fraction of the cylinder submerged in lower liquid.
To solve the problem step by step, we will analyze the forces acting on the wooden cylinder and use the conditions given in the problem.
Step 1: Understand the initial condition
A wooden cylinder of length L floats in a liquid of specific gravity ρ with 13 of its length submerged.
Step 2: Calculate the buoyant force
The buoyant force Fb acting on the cylinder when it is floating is equal to the weight of the liquid displaced by the submerged part of the cylinder.
Fb=Weight of the displaced liquid=ρ1gVs
Where:
- Vs is the volume of the submerged part of the cylinder, which is L3×A (where A is the cross-sectional area).
- ρ1 is the density of the liquid.
Thus, we have:
Fb=ρ1g(L3A)
Step 3: Set up the equilibrium condition
At equilibrium, the buoyant force equals the weight of the wooden cylinder:
Fb=mg
Where m is the mass of the wooden cylinder:
mg=ρwgLA
Where ρw is the density of the wooden cylinder.
Step 4: Equate the forces
Setting the two expressions for buoyant force equal gives:
ρ1g(L3A)=ρwgLA
Canceling g and A from both sides, we get:
ρ1L3=ρwL
This simplifies to:
ρw=ρ13
Step 5: Use the geometric progression condition
It is given that the densities of the liquid at the bottom (ρ2), the cylinder (ρw), and the upper liquid (ρ1) are in geometric progression:
ρ2w=ρ1ρ2
Substituting ρw=ρ13:
(ρ13)2=ρ1ρ2
This simplifies to:
ρ219=ρ1ρ2
Dividing both sides by ρ1 (assuming ρ1≠0) gives:
ρ2=ρ19
Step 6: Analyze the second condition
When the upper liquid is poured in, the cylinder is completely submerged. Let x be the height of the cylinder submerged in the lower liquid (ρ1), and L−x be the height submerged in the upper liquid (ρ2).
The total buoyant force now is:
Fb1+Fb2=mg
Where:
Fb1=ρ1gxA
Fb2=ρ2g(L−x)A
Thus, we have:
ρ1gxA+ρ2g(L−x)A=ρwgLA
Canceling g and A:
ρ1x+ρ2(L−x)=ρwL
Step 7: Substitute known values
Substituting ρw and ρ2:
ρ1x+ρ19(L−x)=ρ13L
Step 8: Solve for x
Expanding and rearranging gives:
ρ1x+ρ19L−ρ19x=ρ13L
Combining terms:
(1−19)ρ1x=(13−19)ρ1L
This simplifies to:
89ρ1x=29ρ1L
Dividing both sides by ρ1 (assuming ρ1≠0):
89x=29L
Thus:
x=28L=L4
Step 9: Find the fraction submerged in the lower liquid
The fraction of the cylinder submerged in the lower liquid is:
xL=L/4L=14
Final Answer
The fraction of the cylinder submerged in the lower liquid is 14.
---
A wooden cylinder of length L floats in a liquid of specific gravity ρ with 13 of its length submerged.
The buoyant force Fb acting on the cylinder when it is floating is equal to the weight of the liquid displaced by the submerged part of the cylinder.
- Vs is the volume of the submerged part of the cylinder, which is L3×A (where A is the cross-sectional area).
- ρ1 is the density of the liquid.
At equilibrium, the buoyant force equals the weight of the wooden cylinder:
Setting the two expressions for buoyant force equal gives:
It is given that the densities of the liquid at the bottom (ρ2), the cylinder (ρw), and the upper liquid (ρ1) are in geometric progression:
When the upper liquid is poured in, the cylinder is completely submerged. Let x be the height of the cylinder submerged in the lower liquid (ρ1), and L−x be the height submerged in the upper liquid (ρ2).
Fb2=ρ2g(L−x)A
Substituting ρw and ρ2:
Expanding and rearranging gives:
The fraction of the cylinder submerged in the lower liquid is:
The fraction of the cylinder submerged in the lower liquid is 14.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - I
6 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
Knowledge Check
A body floats in a liquid A of density ρ1 with a part of it submerged inside liquid while in liquid B of density ρ2 totally submerged inside liquid. The densities ρ1 and ρ2 are related as :
Aρ1=ρ2Bρ1<ρ2Cρ1>ρ2Dnothing can be said
A block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View SolutionHow is the upthrust related to the volume of the body submerged in a liquid?
View SolutionA solid of density D is floating in a liquid of density d. If υ is the volume of solid submerged in the liquid and V is the total volume of the solid, then υ/V equal to
View SolutionA uniform wooden bar of length l and mass m hinged on a vertical wall of a containing water, at one end.

3/5th part of the bar is submerged in water. Find the ratio of densities of the liquid and the bar.
View SolutionAssertion : A solid floats in a liquid so that it is just submerged . When the liquid is heated the solid sinks to the bottom.
Reason : Weight of the solid increases with the rise in temperature .
View SolutionA needle of length l and density ρ will float on a liquid of surface tension σ if its radius r is less than or equal to:
View SolutionA cylinder is floating in two liquids as shown in figure. Choose the correct options.
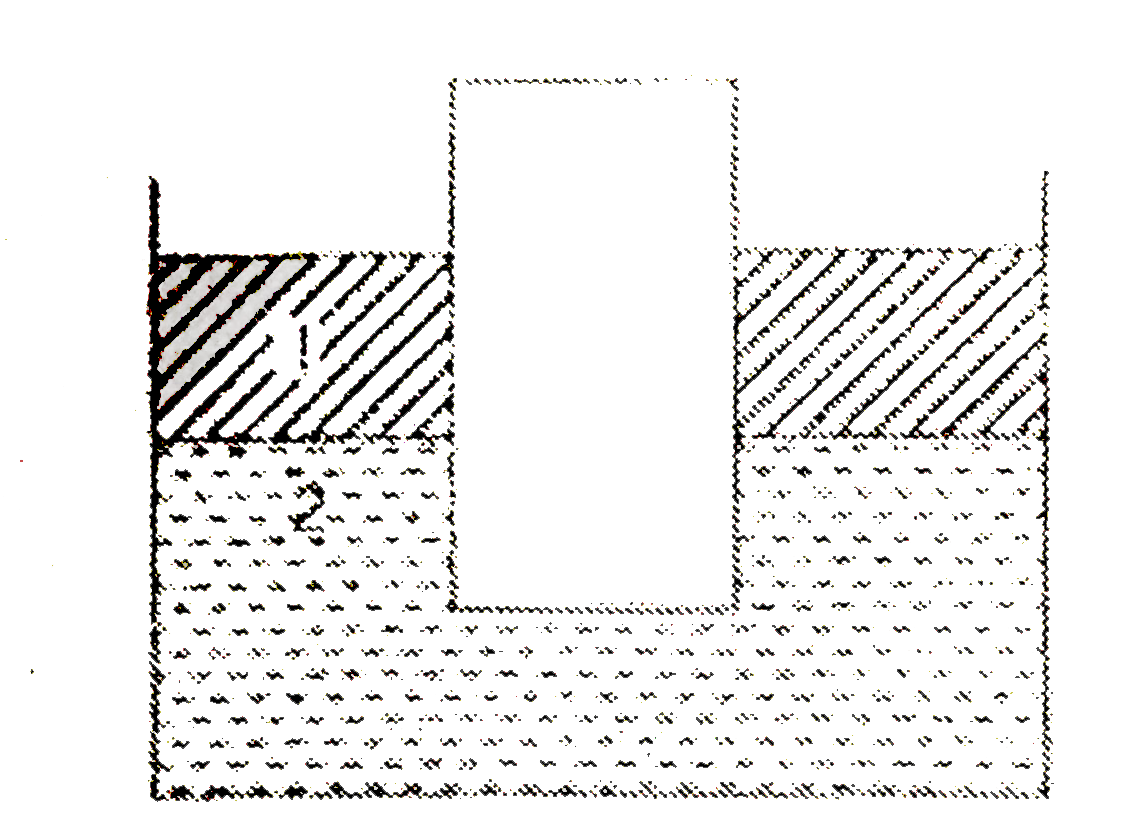
View Solution
