A cylinder vessel of radius 10 cm containing a liquid is rotating about a vertical axis through the centre of circular base. The vessel is rotating with angular frequency 10 rad/s. Find the difference of the heights of liquid at centre of vessel and edge.
To solve the problem of finding the difference in heights of the liquid at the center and the edge of a rotating cylindrical vessel, we can follow these steps:
1. Understand the Setup:
- We have a cylindrical vessel with a radius r=10 cm (which is 0.1 m) rotating about a vertical axis with an angular frequency ω=10 rad/s.
- We need to find the height difference h between the liquid at the center (point A) and at the edge (point B).
2. Apply Bernoulli's Equation:
- For points A (center) and B (edge), we can use Bernoulli's equation, which states:
PA+12ρv2A+ρghA=PB+12ρv2B+ρghB
- Here, P is the pressure, ρ is the density of the liquid, v is the velocity, g is the acceleration due to gravity, and h is the height.
3. Set Up the Equation:
- At the center (point A), the velocity vA=0 and height hA=0 (taking this as our reference point).
- At the edge (point B), we denote the height as hB=h and need to find vB.
4. Simplify the Equation:
- The equation simplifies to:
0+0+0=PB+12ρv2B+ρgh
- Rearranging gives:
12ρv2B+ρgh=PB
5. Find the Velocity at the Edge:
- The velocity at the edge vB can be expressed as:
vB=ωr
- Substituting the values:
vB=10rad/s×0.1m=1m/s
6. Substitute into the Equation:
- Now substituting vB into the equation:
0=PB+12ρ(1)2+ρgh
- Ignoring the pressure term (since it cancels out), we have:
0=12ρ+ρgh
- Rearranging gives:
12=gh
7. Solve for Height:
- Assuming g=10m/s2:
h=1/2g=1/210=0.05m=5cm
Conclusion:
The difference in heights of the liquid at the center and the edge of the vessel is 5cm.
- We have a cylindrical vessel with a radius r=10 cm (which is 0.1 m) rotating about a vertical axis with an angular frequency ω=10 rad/s.
- We need to find the height difference h between the liquid at the center (point A) and at the edge (point B).
- For points A (center) and B (edge), we can use Bernoulli's equation, which states:
PA+12ρv2A+ρghA=PB+12ρv2B+ρghB
- Here, P is the pressure, ρ is the density of the liquid, v is the velocity, g is the acceleration due to gravity, and h is the height.
- At the center (point A), the velocity vA=0 and height hA=0 (taking this as our reference point).
- At the edge (point B), we denote the height as hB=h and need to find vB.
- The equation simplifies to:
0+0+0=PB+12ρv2B+ρgh
- Rearranging gives:
12ρv2B+ρgh=PB
- The velocity at the edge vB can be expressed as:
vB=ωr
- Substituting the values:
vB=10rad/s×0.1m=1m/s
- Now substituting vB into the equation:
0=PB+12ρ(1)2+ρgh
- Ignoring the pressure term (since it cancels out), we have:
0=12ρ+ρgh
- Rearranging gives:
12=gh
- Assuming g=10m/s2:
h=1/2g=1/210=0.05m=5cm
The difference in heights of the liquid at the center and the edge of the vessel is 5cm.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - J
Explore 9 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - H
Explore 5 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment(Section-D)
Explore 14 Videos
Similar Questions
A cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity ω then what is the difference of the heights of liquid at centre of vessel and edge?
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
View SolutionA cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
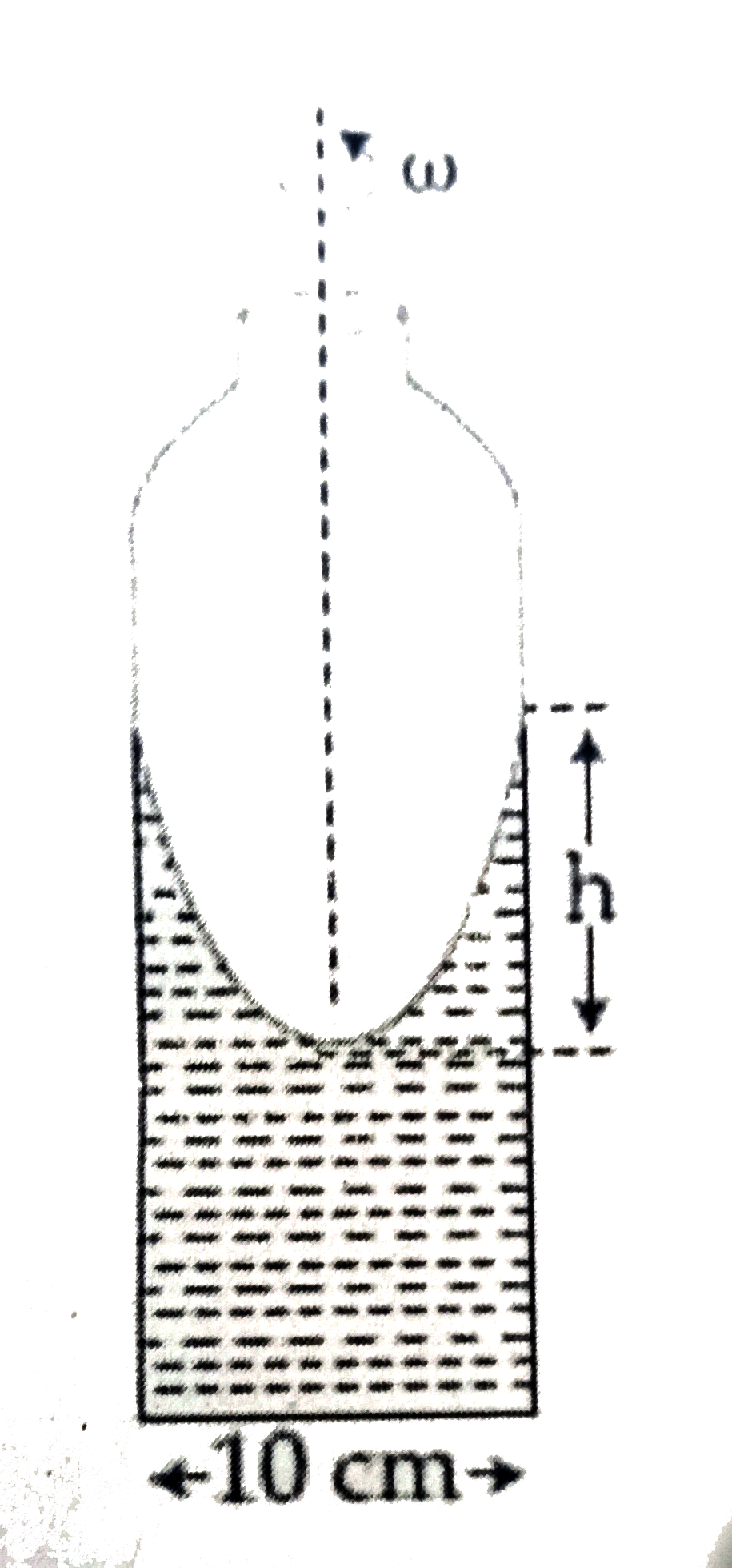
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA cylinder of radius R full of liquid of density p is rotated about its axis at w rad/s. The increase in pressure at the centre of the cylinder will be
View SolutionA long cylindrical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis, the liquid rises up near the wall. If the radius of vessel is 5 cm and its rotational speed is 2 rotations per second, then the difference in the heights between the centre and the sides, in cm, will be:
View Solution