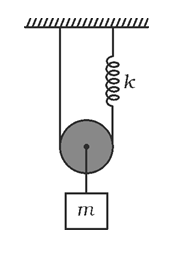
Many builidings have other types of mass dampersas antisway devices ( Refers of Example 14) some like the Johns Honacock building in Boston,have a larger block oscillating at the end of spring and an a lubricated track. .Suppose the block has m=5.44×105kg and is designed to oscillate at a frequency of5√2 Hz and with amplitude xm=0.40m . Find the total mechanical energy E of the spring block system.
Hint :K=mω2=m(2πv)2
E=K+U=12mv2+12kx2
To find the total mechanical energy E of the spring-block system, we can use the formula for total energy in a harmonic oscillator, which is given by:
E=K+U=12mv2+12kx2
Where:
- K is the kinetic energy,
- U is the potential energy,
- m is the mass,
- v is the velocity,
- k is the spring constant,
- x is the displacement.
Step 1: Calculate the angular frequency ω
The angular frequency ω is related to the frequency f by the formula:
ω=2πf
Given that f=5√2Hz:
ω=2π(5√2)=10√2πrad/s
Step 2: Calculate the spring constant k
The spring constant k can be calculated using the formula:
k=mω2
Substituting the values:
k=5.44×105kg×(10√2π)2
Calculating (10√2π)2:
(10√2π)2=100⋅2⋅π2=200π2
Thus,
k=5.44×105×200π2
Step 3: Calculate the total mechanical energy E
The total mechanical energy E at maximum displacement (where kinetic energy is zero and potential energy is maximum) is given by:
E=12kx2m
Substituting xm=0.40m:
E=12(5.44×105×200π2)(0.40)2
Calculating (0.40)2=0.16:
E=12(5.44×105×200π2)(0.16)
E=5.44×105×100π2×0.08
E=5.44×105×8π2
Step 4: Calculate the numerical value
Using π2≈9.87:
E≈5.44×105×8×9.87
Calculating this gives:
E≈5.44×105×79≈4.3×107J
Final Answer
The total mechanical energy E of the spring-block system is approximately:
E≈8.8×107J
---
- K is the kinetic energy,
- U is the potential energy,
- m is the mass,
- v is the velocity,
- k is the spring constant,
- x is the displacement.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION -A)58videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )25videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)13videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)4videos
PHYSICAL WORLD
Similar Questions
Knowledge Check
- Question 1 - Select One
A simple harmonic oscillator has a frequency of 2.5 Hz and an amplitude of 0.05m. What is the period of the oscillations?
A0.4sB0.2sC8sD20s - Question 2 - Select One
Assertion: A block of small mass m attached to a stiff spring will have large oscillation frequency.
Reason: Stiff springs have high value of spring constant.AIf both assertion and reson are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
An object of mass 1kg executes simple harmonic oscillations along the x-axis, with a frequency of 2πHz. At the position x = 1 m, the object has a kinetic energy of 24 J. The amplitude of the oscillation is
View SolutionIn a place e.m wave, the electric field oscillates sinusoidally at a frequency of 2.5×1010Hz and amplitude 480V/m.The amplitude of oscillating magnetic field will be,
View SolutionA block of mass 0.5 kg hanging from a vertical spring executes simple harmonic motion of amplitude 0.1 m and time period 0.314s. Find the maximum fore exerted by the spring on the blockl.
View SolutionIn the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
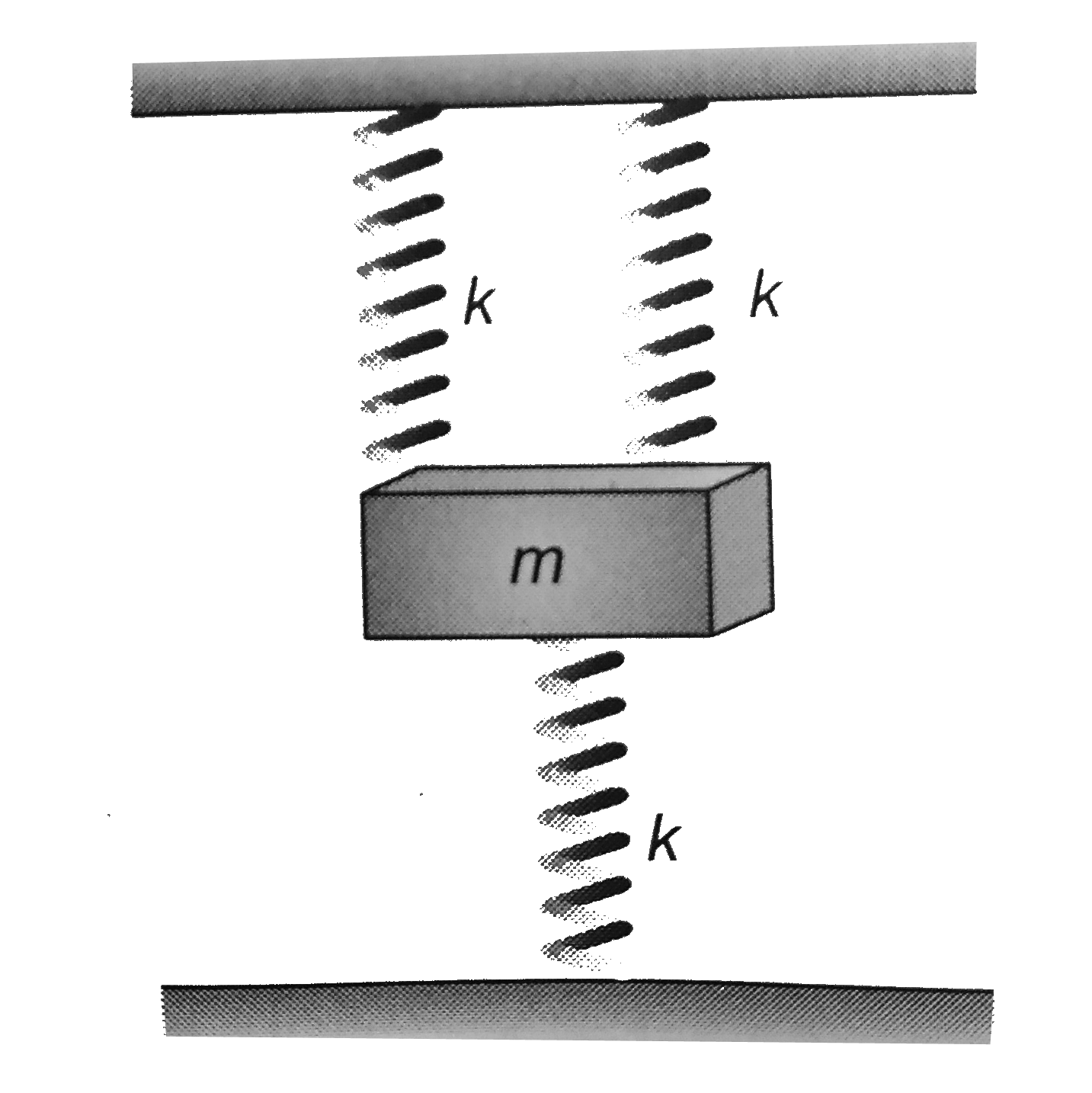 View Solution
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
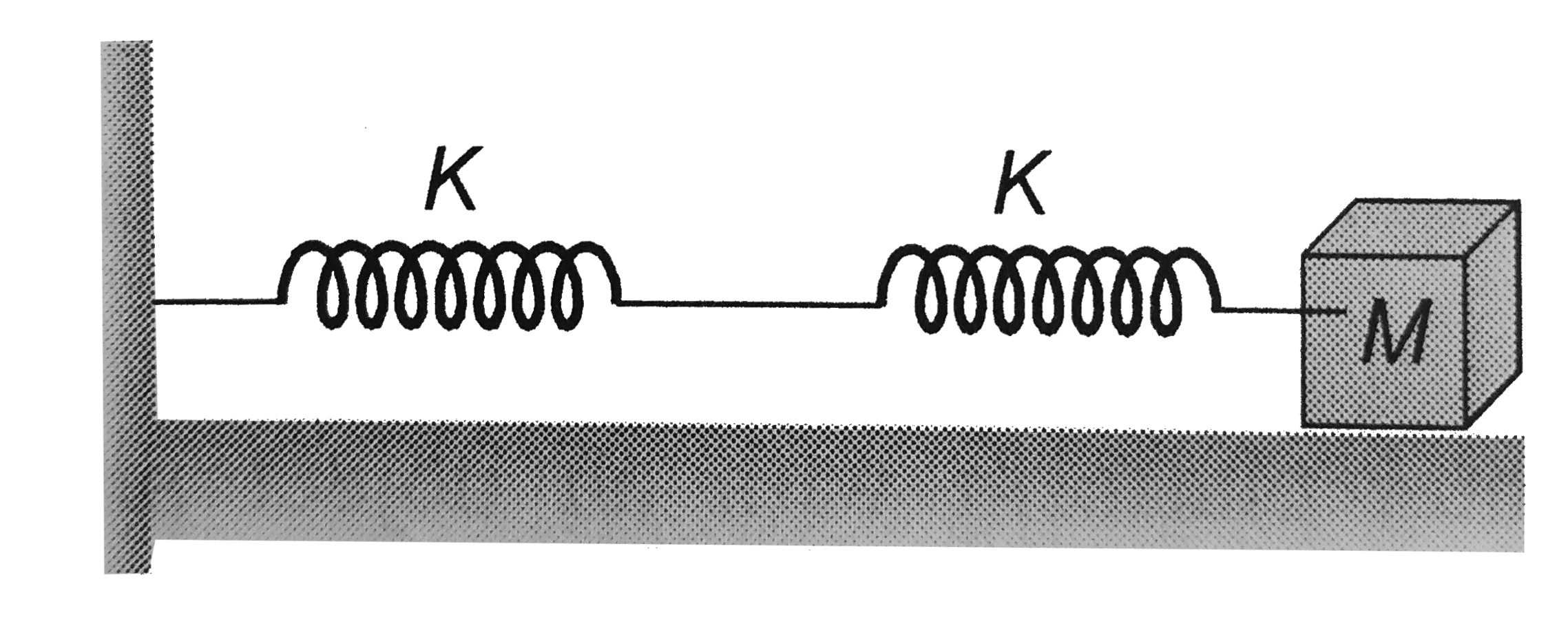 View Solution
View SolutionA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be
 View Solution
View Solution