STATEMENT -1 : If a simple pendulum is in a carriage which is accelerating downward and acceleration is greater than acceleration due to gravity , then pendulum turns up side down and oscillates about highest point.
and
STATEMENT -2 : The time period of pendulum will be independent of g in above case of pendulum oscillating about highest point.
The correct Answer is:3
To solve the question, we need to analyze both statements provided and determine their validity based on the principles of physics related to oscillations and pendulums.
Step 1: Analyze Statement 1
Statement 1: If a simple pendulum is in a carriage which is accelerating downward and the acceleration is greater than the acceleration due to gravity, then the pendulum turns upside down and oscillates about the highest point.
- When the carriage accelerates downward with an acceleration greater than g (acceleration due to gravity), the effective gravitational force acting on the pendulum becomes negative. This means that the pendulum will not be able to hang downwards as it normally would. Instead, it will turn upside down and oscillate about the highest point (the position where it is inverted).
Conclusion for Statement 1: This statement is true.
Step 2: Analyze Statement 2
Statement 2: The time period of the pendulum will be independent of g in the above case of the pendulum oscillating about the highest point.
- The time period T of a simple pendulum is given by the formula:
T=2π√Lgeffective
where geffective is the effective acceleration acting on the pendulum. When the carriage is accelerating downward with an acceleration a greater than g, the effective acceleration can be expressed as:
geffective=a−g
- Therefore, the time period will depend on both the length L of the pendulum and the effective gravitational acceleration geffective. Since geffective is influenced by g, the time period is not independent of g.
Conclusion for Statement 2: This statement is false.
Final Conclusion
- Statement 1 is true.
- Statement 2 is false.
Statement 1: If a simple pendulum is in a carriage which is accelerating downward and the acceleration is greater than the acceleration due to gravity, then the pendulum turns upside down and oscillates about the highest point.
Conclusion for Statement 1: This statement is true.
Statement 2: The time period of the pendulum will be independent of g in the above case of the pendulum oscillating about the highest point.
T=2π√Lgeffective
where geffective is the effective acceleration acting on the pendulum. When the carriage is accelerating downward with an acceleration a greater than g, the effective acceleration can be expressed as:
geffective=a−g
- Therefore, the time period will depend on both the length L of the pendulum and the effective gravitational acceleration geffective. Since geffective is influenced by g, the time period is not independent of g.
- Statement 1 is true.
- Statement 2 is false.
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-F( MATRIX MATCH TYPE QUESTIONS) )
3 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( Section-G( Integers Answer Type Question) )
4 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION -D( Comprehension) )
3 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
An oscillating simple pendulum is kept in a lift which is accelerating upwards. Will there be any change in the time period ?
View SolutionA simple pendulum is suspended from the ceiling a car accelerating uniformly on a horizontal road. If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
View Solution
Knowledge Check
A simple pendulum with a bob of mass m oscillates from A to C and back to A such that PB is H. IF the acceleration due to gravity is g, the velocity of bob as it passes through B is
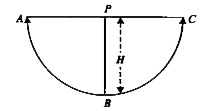 AzeroB2g HCmghD√(2gH)
AzeroB2g HCmghD√(2gH)
The time period of simple pendulum inside a stationary lift is T. If lift starts accelerating upwards with the acceleration of g/2, then the new time period of the simple pendulum will be
View SolutionA simple pendulum of length 'L' has mass 'M' and it oscillates freely with amplitude A, Energy is
(g = acceleration due to gravity)
View SolutionCalculate the time period of a simple pendulum of length one meter. The acceleration due to gravity at the place is π2ms−2.
View SolutionIn an experiment of determine acceleration due to gravity by simple pendulum, a student commits 1% positive error in the measurement of length and 3% negative error in the time then % error in g will be
View SolutionThe time period of a simple pendulum on the surface of the Earth is T1 and that on the planet Mars is T2. If T2<T, then acceleration due to gravity on Mars is
View SolutionThe time period of a simple pendulum of length L as measured in an elevator descending with acceleration g / 3 is
View SolutionState how does the time period of a simple pendulum depend on acceleration due to gravity.
View Solution
