A simple pendulum of length 'L' has mass 'M' and it oscillates freely with amplitude A,
Energy is
(g = acceleration due to gravity)
MgA22L
MgA2L
MgA2L
2MgA2L
The correct Answer is:A
To find the total energy of a simple pendulum of length L, mass M, and amplitude A, we can follow these steps:
Step 1: Understand the Energy in Simple Harmonic Motion
In simple harmonic motion (SHM), the total mechanical energy E is the sum of kinetic energy K and potential energy U. The total energy remains constant throughout the motion.
Step 2: Identify Energy at Extreme Position
At the extreme position of the pendulum's swing (where it momentarily comes to rest), all the energy is potential energy. Therefore, we can express the total energy as:
E=U=Potential Energy at the extreme position
Step 3: Calculate Potential Energy
The potential energy U at the maximum height (extreme position) can be calculated using the formula:
U=Mgh
where h is the height raised from the lowest point.
Step 4: Determine Height h
The height h can be determined using the geometry of the pendulum. When the pendulum is at its maximum amplitude A, the height h can be expressed as:
h=L−Lcos(θ)=L(1−cos(θ))
For small angles, we can approximate cos(θ) using the small angle approximation cos(θ)≈1−A22L. Thus,
h≈A22L
Step 5: Substitute h into Potential Energy Formula
Substituting h into the potential energy formula gives:
U=Mg(A22L)
Step 6: Total Energy Expression
Thus, the total energy E of the pendulum can be expressed as:
E=U=MgA22L
Final Answer
The total energy of the simple pendulum is:
E=MgA22L
---
In simple harmonic motion (SHM), the total mechanical energy E is the sum of kinetic energy K and potential energy U. The total energy remains constant throughout the motion.
At the extreme position of the pendulum's swing (where it momentarily comes to rest), all the energy is potential energy. Therefore, we can express the total energy as:
E=U=Potential Energy at the extreme position
The potential energy U at the maximum height (extreme position) can be calculated using the formula:
U=Mgh
where h is the height raised from the lowest point.
The height h can be determined using the geometry of the pendulum. When the pendulum is at its maximum amplitude A, the height h can be expressed as:
h=L−Lcos(θ)=L(1−cos(θ))
For small angles, we can approximate cos(θ) using the small angle approximation cos(θ)≈1−A22L. Thus,
h≈A22L
Substituting h into the potential energy formula gives:
U=Mg(A22L)
Thus, the total energy E of the pendulum can be expressed as:
E=U=MgA22L
The total energy of the simple pendulum is:
E=MgA22L
Similar Questions
A simple pendulum of length L and mass M is oscillating about a vertical line with angular amplitude θ. If for an angular displacement ϕ(ϕ>θ) the tension in the string is T1 and for angular amplitude θ the tension is T2, then
View SolutionA simple pendulum of length 1m is allowed to oscillate with amplitude 2∘. it collides at T to the vertical its time period will be (use g=π2)
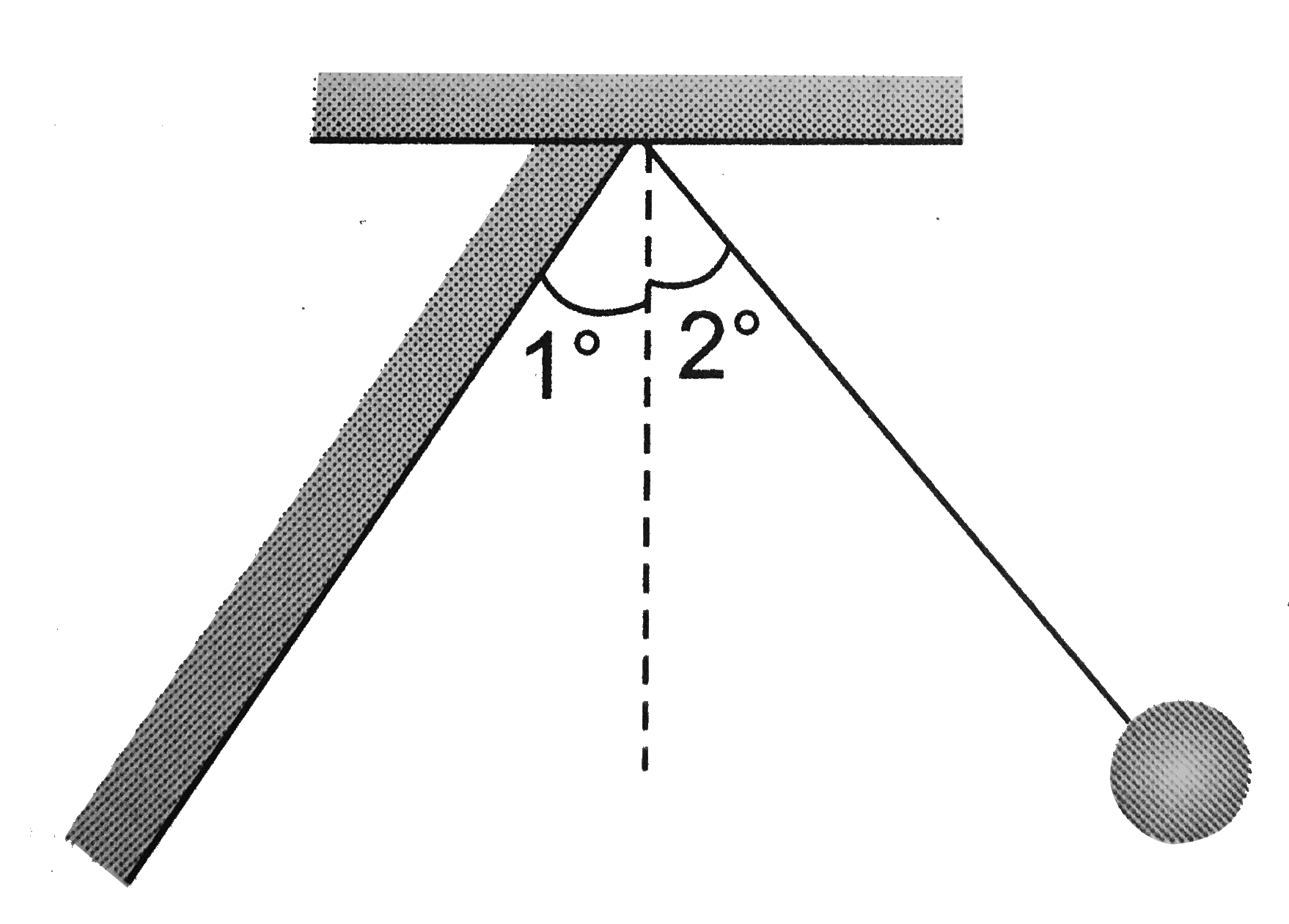
View Solution
Knowledge Check
A simple pendulum with a bob of mass m oscillates from A to C and back to A such that PB is H. IF the acceleration due to gravity is g, the velocity of bob as it passes through B is
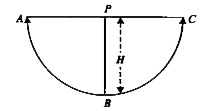 AzeroB2g HCmghD√(2gH)
AzeroB2g HCmghD√(2gH)
A simple pendulum of length 1 m with a bob of mass m swings with an angular amplitude 30∘. Then (g=9.8m/s2
View SolutionA simple pendulm has a length L and a bob of mass M. The bob is vibrating with amplitude a .What is the maximum tension in the string?
View SolutionFind the binding energy of a satellite of mass m in orbit of radius r, (R = radius of earth, g = acceleration due to gravity)
View SolutionA simple pendulum of length L has a period T. If length is changed by ΔL, the change in period ΔT is proportional to
View SolutionIf unit of length and time is double, dthe numerical valuure of 'g' (acceleration due to gravity) will be
View SolutionThe time period Of oscillation of a simple pendulum depends on the following quantities
Length of the pendulum (l),
Mass of the bob (m), and
Acceleration due to gravity (g)
Derive an expression for Using dimensional method.
View SolutionA simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
View Solution
