Calculate the Poisson's ratio for steel. Given that Young's modulus is 2×1011Nm−2 and rigidity modulus is 8×1010Nm−2.
The correct Answer is:0.25
To calculate the Poisson's ratio for steel, we will use the relationship between Young's modulus (E), rigidity modulus (G), and Poisson's ratio (σ). The formula we will use is:
E=3G(1−2σ)
Where:
- E is Young's modulus,
- G is the rigidity modulus,
- σ is Poisson's ratio.
1. Identify the given values:
- Young's modulus E=2×1011N/m2
- Rigidity modulus G=8×1010N/m2
2. Write down the relationship:
E=3G(1−2σ)
3. Substitute the known values into the equation:
2×1011=3×(8×1010)×(1−2σ)
4. Calculate 3G:
3G=3×(8×1010)=24×1010
5. Rearranging the equation:
2×1011=24×1010×(1−2σ)
6. Divide both sides by 24×1010:
2×101124×1010=1−2σ
7. Simplify the left side:
224=112
So,
112=1−2σ
8. Rearranging to find 2σ:
2σ=1−112
9. Finding a common denominator:
1=1212
Thus,
2σ=1212−112=1112
10. Finally, solve for σ:
σ=1124
11. Calculating the numerical value:
σ≈0.4583
Final Answer:
The Poisson's ratio for steel is approximately σ≈0.4583.
- E is Young's modulus,
- G is the rigidity modulus,
- σ is Poisson's ratio.
- Young's modulus E=2×1011N/m2
- Rigidity modulus G=8×1010N/m2
E=3G(1−2σ)
2×1011=3×(8×1010)×(1−2σ)
3G=3×(8×1010)=24×1010
2×1011=24×1010×(1−2σ)
2×101124×1010=1−2σ
224=112
So,
112=1−2σ
2σ=1−112
1=1212
Thus,
2σ=1212−112=1112
σ=1124
σ≈0.4583
The Poisson's ratio for steel is approximately σ≈0.4583.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY) FROM WORK DONE IN STRETCHING A WIRE4videos
PROPERTIES OF MATTER
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 2(SURFACE TENSIONS)SHORT ANSWER QUESTIONS WITH ANSWERS14videos
PROPERTIES OF MATTER
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY) FROM BULK MODULUS8videos
PROPERTIES OF MATTER
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)2videos
OSCILLATIONS
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D12videos
SAMPLE QUESTION PAPER - 01
Similar Questions
The Youngg's modulus of a material is 6×1010Nm−2 and its bulk modulus is 2.8×1010Nm−2 . What is its Poisson's ratio ?
View SolutionA Copper wire of length 2.2m and a steel wire of length 1.6m, both of diameter 3.0mm are connected end to end. When stretched by a load, the net elongation is found to be 0.70 mm. Obtain the load applied . Young's modulus of copper is 1.1×1011Nm−2 and Young's modulus of steel is 2.0×1011Nm−2.
View Solution
Knowledge Check
- Question 1 - Select One
For a given material, Young's modulus is 2.4 times that of rigidity modulus. Its Poisson's ratio is
A2.4B1.2C0.4D0.2
Calculate the speed of longitudinal wave in steel. Young's modulus for steel is 3×1010N/m2 and its density 1.2×103kg/m3
View SolutionCalculate the speed of longitudinal wave in steel. Young's modulus for steel is 3×1010N/m2 and its density 1.2×103kg/m3
View SolutionA light rod AC of length 2.00 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10−3m2 and the other is of brass of cross-section 2×10−3m2. The position of point D from end A along the rod at which a weight may be hung to produce equal stress in both the wires is [Young's modulus of steel is 2×1011Nm2 and for brass is 1×1011Nm−2]
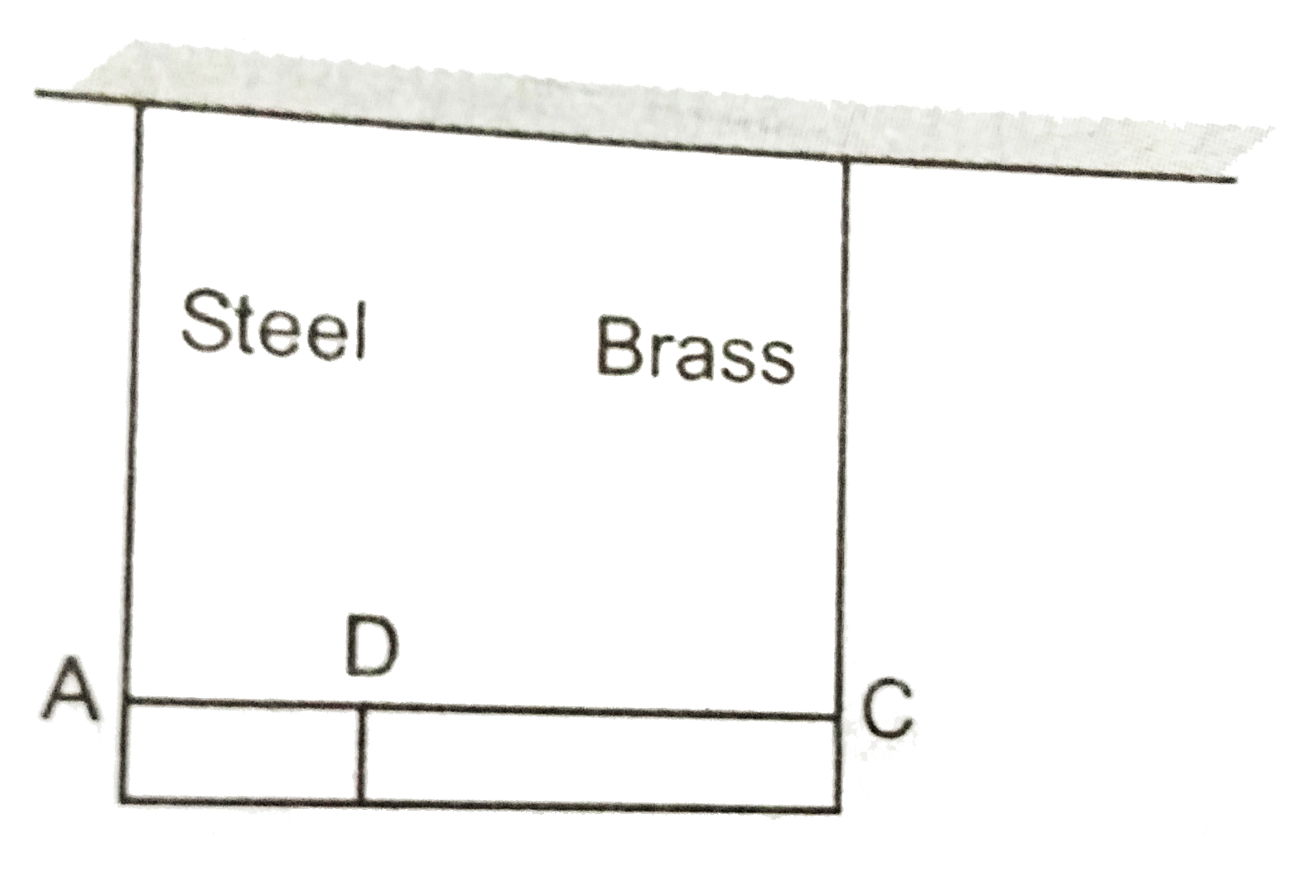 View Solution
View SolutionA composite wire of uniform diameter 3mm consisting of copper wire of length 2.2 m and a steel wire of length 1. 6m stretches under a load by 0.7mm. Calcualte the load, given that the Young's modulus of copper is 1.1×1011Pa and for steel is 2.0×1011Pa.
View SolutionThe Young's modulus of brass is 9.1×1010N/m2and its rigidity modulus is 3.5×1010N/m2. Calculate its Poisson's ratio ?
View SolutionYoung 's modulus of steel is 2.0×1011Nm/(2). Express it is dynecm2.
View SolutionCalculate the work done in streching a steel wire of Young's modulus of 2×1011Nm−2 mass of 40kg,length of 200 cm and area of cross-section is 0.06 cm2 slowly applied without the elastic limit being reached.
View Solution

