Question

$x(x,t)=\frac{0.8}{[{(4x+5t)}^2+5]}$, represents a moving pulse where x and y are in metre and t is in second. Find
(i) The direction of wave propagation.
(ii) The wave speed.
(iii) The maximum displacement from the mean position (i.e., the aplitude of the wave).
(iv). Whether the wave pulse is symmetric or not.

Explanation

To solve the given problem, we will analyze the function $$f(x,t)=\frac{0.8}{(4x+5t{)}^2+5}$$ step by step.

Step 1: Determine the direction of wave propagation
The general form of a wave function can be expressed as \( f(x, t) = A \cdot g(kx - \omega t) \) or \( f(x, t) = A \cdot g(kx + \omega t) \). Here, \( g \) is some function, \( A \) is the amplitude, \( k \) is the wave number, and \( \omega \) is the angular frequency.

In our case, we can identify the argument of the function as \( 4x + 5t \). The coefficient of \( x \) is positive (4), and the coefficient of \( t \) is also positive (5). This indicates that the wave is propagating in the negative x-direction.

Direction of wave propagation: Negative x-axis.

Step 2: Calculate the wave speed
The wave speed \( v \) can be calculated using the formula:

\( v = \frac{\text{Coefficient of } t}{\text{Coefficient of } x} = \frac{b}{a} \)

Where \( b \) is the coefficient of \( t \) (which is 5) and \( a \) is the coefficient of \( x \) (which is 4).

\( v = \frac{5}{4} \, \text{m/s} = 1.25 \, \text{m/s} \)

Wave speed: 1.25 m/s.

Step 3: Find the maximum displacement (amplitude)
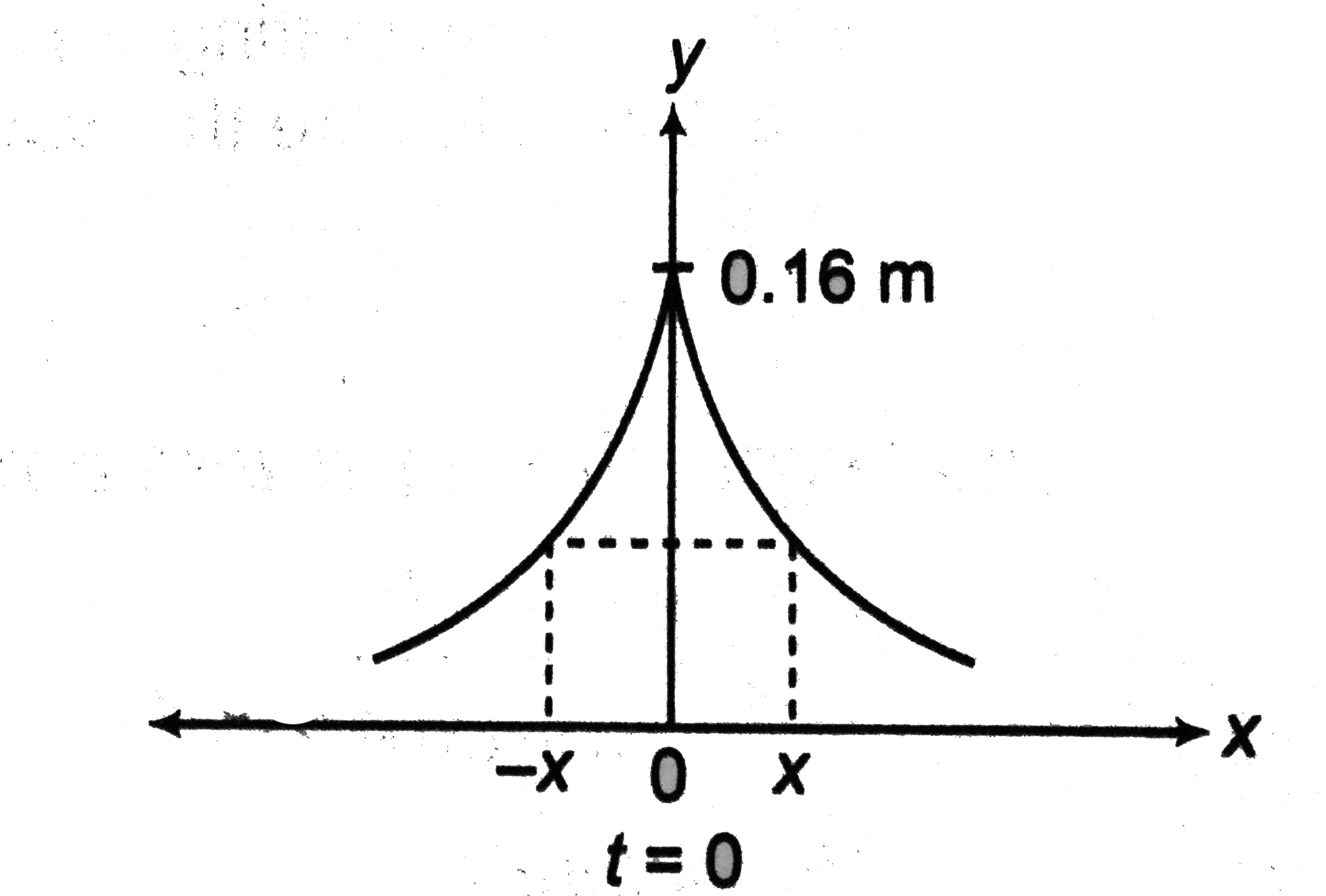
The maximum displacement (amplitude) occurs when the denominator of the function is minimized. The denominator is minimized when \( (4x + 5t)^2 \) is minimized, which occurs when \( 4x + 5t = 0 \).

Substituting \( 4x + 5t = 0 \) into the function gives:

\( f(x, t) = \frac{0.8}{0 + 5} = \frac{0.8}{5} = 0.16 \, \text{m} \)

Maximum displacement (amplitude): 0.16 m.

Step 4: Determine if the wave pulse is symmetric
To check for symmetry, we can evaluate the function at \( t = 0 \):

\( f(x, 0) = \frac{0.8}{(4x)^2 + 5} = \frac{0.8}{16x^2 + 5} \)

The function \( f(x, 0) \) is symmetric about \( x = 0 \) because \( f(x, 0) = f(-x, 0) \). This indicates that the graph of the function is symmetric.

Wave pulse is symmetric.

Summary of Answers:
(i) Direction of wave propagation: Negative x-axis.
(ii) Wave speed: 1.25 m/s.
(iii) Maximum displacement (amplitude): 0.16 m.
(iv) The wave pulse is symmetric.