A wave front is represented by the plane y=5−x Find the direction of propagation of wave.
To determine the direction of propagation of a wave given the wave front represented by the equation y=5−x, we can follow these steps:
1. Identify the Equation of the Wave Front:
The wave front is given by the equation:
y=5−x
This can be rearranged to:
x+y=5
This represents a straight line in the xy-plane.
2. Determine the Slope of the Wave Front:
The slope m of the line can be determined from the equation y=mx+c. Here, the slope is:
m=−1
This means that for every unit increase in x, y decreases by 1 unit.
3. Calculate the Angle with the X-axis:
The angle θ that the line makes with the positive x-axis can be calculated using the tangent function:
tan(θ)=slope=−1
Therefore, the angle θ is:
θ=tan−1(−1)=135∘(in the second quadrant)
4. Determine the Direction of Propagation:
The direction of wave propagation is always perpendicular to the wave front. The angle of propagation ϕ can be found by adding 90∘ to the angle of the wave front:
ϕ=135∘+90∘=225∘
However, to find the angle with respect to the x-axis, we can also consider the negative slope which indicates that the wave propagates in the direction opposite to the slope of the wave front.
5. Final Direction of Propagation:
The direction of propagation of the wave is at an angle of 45∘ with respect to the x-axis (in the third quadrant), which corresponds to the direction of the wave moving away from the wave front.
Conclusion:
The direction of propagation of the wave is at an angle of 45∘ with respect to the positive x-axis.
The wave front is given by the equation:
y=5−x
This can be rearranged to:
x+y=5
This represents a straight line in the xy-plane.
The slope m of the line can be determined from the equation y=mx+c. Here, the slope is:
m=−1
This means that for every unit increase in x, y decreases by 1 unit.
The angle θ that the line makes with the positive x-axis can be calculated using the tangent function:
tan(θ)=slope=−1
Therefore, the angle θ is:
θ=tan−1(−1)=135∘(in the second quadrant)
The direction of wave propagation is always perpendicular to the wave front. The angle of propagation ϕ can be found by adding 90∘ to the angle of the wave front:
ϕ=135∘+90∘=225∘
However, to find the angle with respect to the x-axis, we can also consider the negative slope which indicates that the wave propagates in the direction opposite to the slope of the wave front.
The direction of propagation of the wave is at an angle of 45∘ with respect to the x-axis (in the third quadrant), which corresponds to the direction of the wave moving away from the wave front.
The direction of propagation of the wave is at an angle of 45∘ with respect to the positive x-axis.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If E and B represent electric and magnetic field vectors of the electromagnetic wave, the direction of propagation of eletromagnetic wave is along.
A→EB→BC→B×→ED→E×→B
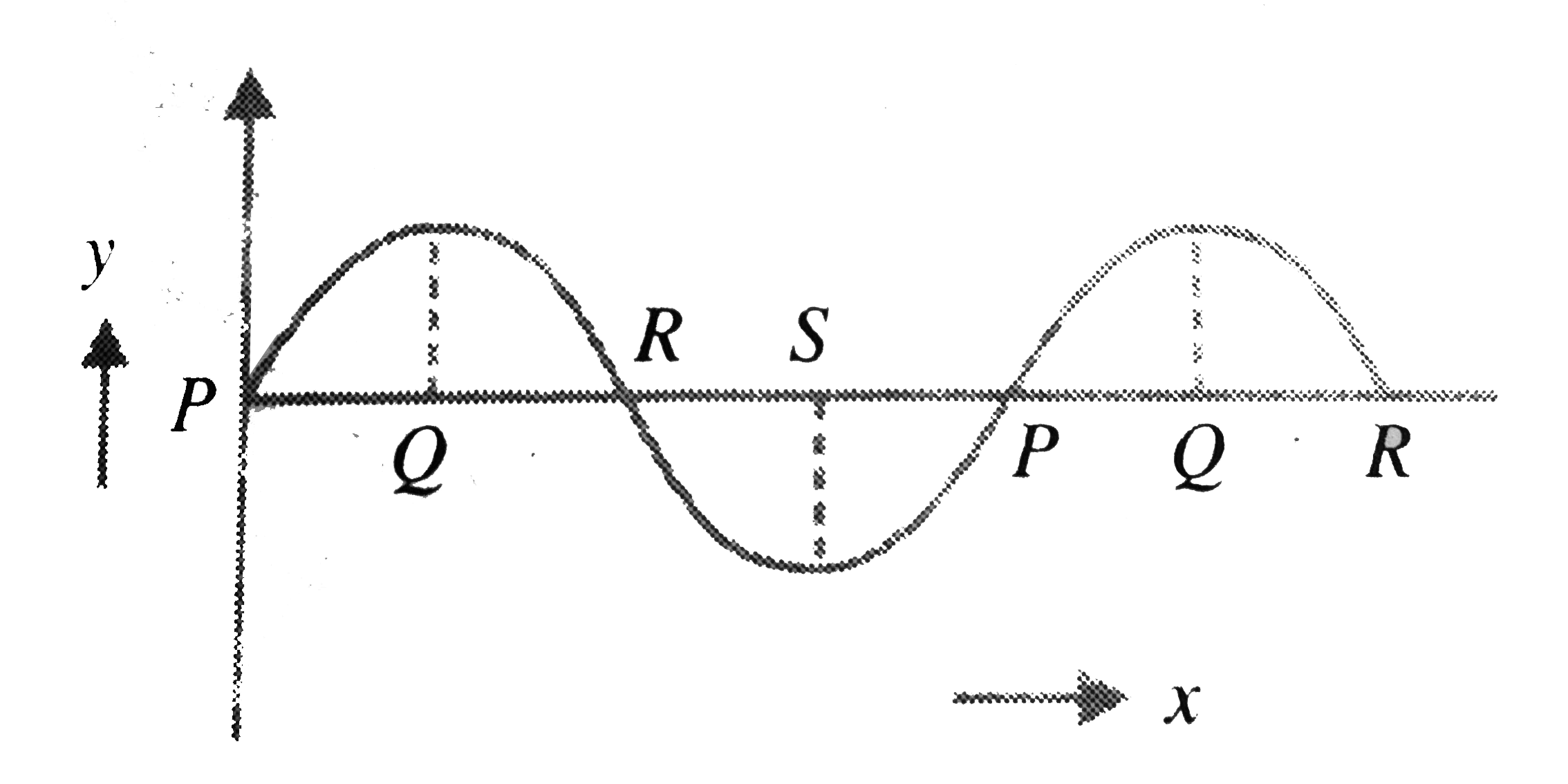
Figure. Represents the displacement y versus distance x along the direction of propagation of a longitudinal wave. The pressure is maximum at position markedView SolutionGround Wave Propagation
View SolutionIf the directions of electric and magnetic field vectors of a plane electromagnetic wave are along positive y- direction and positive z-direction respectively , then the direction of propagation of the wave is along
View SolutionThe equation below represents a progressive wave y=3×10−7sin(8500t−25x)
where t is in seconds x and y in metres. Calculate the speed of the wave and the direction of propagation.View SolutionIf E and B represent electric and magnetic field vectors of the electromagnetic wave, the direction of propagation of eletromagnetic wave is along.
View SolutionIf E and B represent electric and magnetic field vectors of the electromagnetic wave, the direction of propagation of eletromagnetic wave is along.
View SolutionPlane wave front is not produced by a
View Solution

