Write down the equation of progressive wave travelling along the negative X-axis and having an amplitude of 0.21m frequency of 225 Hz nd a wavelength of 0.6 m.
To find the equation of a progressive wave traveling along the negative X-axis with the given parameters, we can follow these steps:
Step 1: Identify the General Equation
The general equation for a wave traveling in the positive X-axis is:
y=asin(ωt−kx)
For a wave traveling in the negative X-axis, the equation becomes:
y=asin(ωt+kx)
Step 2: Given Parameters
From the problem, we have:
- Amplitude a=0.21m
- Frequency f=225Hz
- Wavelength λ=0.6m
Step 3: Calculate Angular Frequency ω
The angular frequency ω is given by:
ω=2πf
Substituting the value of frequency:
ω=2π×225=450πrad/s
Step 4: Calculate Wave Number k
The wave number k is given by:
k=2πλ
Substituting the value of wavelength:
k=2π0.6=2π×106=10π3rad/m
Step 5: Write the Equation of the Wave
Now, substituting the values of a, ω, and k into the equation for a wave traveling in the negative X-axis:
y=0.21sin(450πt+10π3x)
Final Equation
Thus, the equation of the progressive wave traveling along the negative X-axis is:
y=0.21sin(450πt+10π3x)
---
The general equation for a wave traveling in the positive X-axis is:
y=asin(ωt−kx)
For a wave traveling in the negative X-axis, the equation becomes:
y=asin(ωt+kx)
From the problem, we have:
- Amplitude a=0.21m
- Frequency f=225Hz
- Wavelength λ=0.6m
The angular frequency ω is given by:
ω=2πf
Substituting the value of frequency:
ω=2π×225=450πrad/s
The wave number k is given by:
k=2πλ
Substituting the value of wavelength:
k=2π0.6=2π×106=10π3rad/m
Now, substituting the values of a, ω, and k into the equation for a wave traveling in the negative X-axis:
y=0.21sin(450πt+10π3x)
Thus, the equation of the progressive wave traveling along the negative X-axis is:
y=0.21sin(450πt+10π3x)
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - Assignment (Section-A)55videos
WAVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - Assignment (Section-B)35videos
WAVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))12videos
WAVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))1videos
WAVE OPTICS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)13videos
WORK, ENERGY AND POWER
Similar Questions
Knowledge Check
- Question 1 - Select One or More
A wave is represented by the equation
y=Asin(10πx+15πt+π/3)
Where x is in metre and t is in second.
a wave travelling in the positive x-direction with a velocity of 1.5 m/s
a wave travelling in the negative x-direction with a velocity 1.5 m/s
a wave travelling in the negative x-direction with a wavelength of 0.2 m
a wave travelling in the positive x-direction with a wavelength 0.2 mAa wave travelling in the positive x-direction with a velocity of 1.5 m/sBa wave travelling in the negative x-direction with a velocity 1.5 m/sCa wave travelling in the negative x-direction with a wavelength of 0.2 mDa wave travelling in the positive x-direction with a wavelength 0.2 m
The equation of a wave travelling along the positive x-axis, as shown in figure at t = 0 is given by
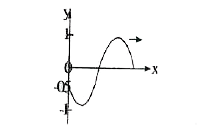 View Solution
View SolutionA harmonic wave has been set up on a very long string which travels along the length of string. The wave has frequency of 50 Hz. Amplitude 1 cm and wavelength 0.5 m. for the above described wave.
Statement (i): time taken by a point on the string to travel a distance of 8 m along the length of string is 0.32 s.
Statement (ii): time taken by a point in the string to travel a distance of 8m, once the wave has reached at that point and sets it into motion is 0.32 s.View SolutionA particle executing S.H.M. having amplitude 0.01 m and frequency 60 Hz. Determine maximum acceleration of particle.
View SolutionAn harmonic wave has been set up on a very long string which travels along the length of the string. The wave has a frequency of 50 Hz, amplitude 1 cm and wavelength 0.5 m. find
(a) the time taken by the wave to travel a distance of 8 m along the length of string (b) the time taken by a point on the string to travel a distance of 8 m, once the wave has reached the point and sets it into motion (c ) also. consider the above case when the amplitude gets doubledView SolutionA body is vibrating in simple harmonic motion with an amplitude of 0.06 m and frequency of 15 Hz . The velocity and acceleration of body is
View SolutionA progressive wave of frequency 500 Hz is travelling with a velocity of 360 m/s. How far apart are two points 60∘ out of phase ?
(ii)Does the speed of a plane-progressive wave depend on the amplitude ?
(iii)The equation of a progressive wave is represented by Y=Asin2(kx−ωt). Find its amplitude and frequency
(iv)Which of the following equations represents a wave travelling along positive y-axis ? (a)x=5 sin (2y-6t) (b) y=6sin (7x-5t) (c ) y=10 sin (6y) cos (8t)View SolutionThe position of a transverse wave travelling in medium along positive x-axis is shown in figure at time t=0. Speed of wave is v=200 m/s
Frequency of the wave is
 View Solution
View Solution


