A wave is described by y=Asin(ωt−kx). The speeds of which of the following particles in the medium are increasing at time t=0?
a.x=0
x=π4k
c.x=π2k
d.x=3π4k
The correct Answer is:B, C
To solve the problem of determining which particles in the medium have increasing speeds at time t=0, we will analyze the wave function given by:
y=Asin(ωt−kx)
Step 1: Determine the velocity of the particles
The velocity v of the particles in the medium can be found by taking the partial derivative of y with respect to time t:
v=∂y∂t=Aωcos(ωt−kx)
At t=0:
v=Aωcos(−kx)=Aωcos(kx)
Step 2: Determine the acceleration of the particles
The acceleration a can be found by taking the derivative of the velocity with respect to time:
a=∂v∂t=−Aω2sin(ωt−kx)
At t=0:
a=−Aω2sin(−kx)=Aω2sin(kx)
Step 3: Analyze conditions for increasing speed
A particle's speed is increasing when the velocity and acceleration have the same sign. Therefore, we need to analyze the signs of v and a:
1. For x=0:
- v=Aωcos(0)=Aω (positive)
- a=Aω2sin(0)=0 (neither positive nor negative)
- Conclusion: Speed is constant.
2. For x=π4k:
- v=Aωcos(π4)=Aω⋅1√2 (positive)
- a=Aω2sin(π4)=Aω2⋅1√2 (positive)
- Conclusion: Speed is increasing.
3. For x=π2k:
- v=Aωcos(π2)=0 (zero)
- a=Aω2sin(π2)=Aω2 (positive)
- Conclusion: Speed is increasing (from zero).
4. For x=3π4k:
- v=Aωcos(3π4)=−Aω⋅1√2 (negative)
- a=Aω2sin(3π4)=Aω2⋅1√2 (positive)
- Conclusion: Speed is decreasing.
Final Conclusion
The particles with increasing speeds at t=0 are located at:
- x=π4k (both velocity and acceleration are positive)
- x=π2k (velocity is zero, but acceleration is positive)
Thus, the correct options are B and C.
- v=Aωcos(0)=Aω (positive)
- a=Aω2sin(0)=0 (neither positive nor negative)
- Conclusion: Speed is constant.
- v=Aωcos(π4)=Aω⋅1√2 (positive)
- a=Aω2sin(π4)=Aω2⋅1√2 (positive)
- Conclusion: Speed is increasing.
- v=Aωcos(π2)=0 (zero)
- a=Aω2sin(π2)=Aω2 (positive)
- Conclusion: Speed is increasing (from zero).
- v=Aωcos(3π4)=−Aω⋅1√2 (negative)
- a=Aω2sin(3π4)=Aω2⋅1√2 (positive)
- Conclusion: Speed is decreasing.
- x=π4k (both velocity and acceleration are positive)
- x=π2k (velocity is zero, but acceleration is positive)
Topper's Solved these Questions
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:Assignment (Section-D)
Explore 9 Videos
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:Assignment (Section-E) Assertion & Reason
Explore 12 Videos
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:Assignment (Section-B)
Explore 35 Videos
- WAVE OPTICSBook:AAKASH INSTITUTE ENGLISHChapter:WAVE OPTICSExercise:Assignment (Section-J (Aakash Challengers question))
Explore 1 Video
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:Assignment (SECTION - D)
Explore 13 Videos
Similar Questions
An electromagnetic wave going through vacuum is described by
E=E0sin(kx−ωt). Which of the following is/are independent of the wavelength?
View SolutionFor a wave described by y=Asin(ωt−kx), consider the following or not and in what direction and describe whether the particle is speeding up, slowing sown or instantanteously not accelerating?

View Solution
Knowledge Check
A transverse wave is represented by y=Asin(ωt−kx). For what value of the wavelength is the wave velocity equal to the maximum particle velocity?
AπA2BπAC2πADAThe displacement of a progressive wave is represented by y=Asin(ωt−kx) where x is distance and t is time. The dimensions of ωk are same as those of
AvelocityBwave numberCwavelengthDfrequencyA travelling wave represented by
y=Asin(ωt−kx)
is superimposed on another wave represented by
y=Asin(ωt+kx). The resultant isAstanding wave having nodes at x=(n+12)λ2, n=0,1,2,….Bsatnding wave having nodes at x=nλ2,n=0,1,2..Cwave travelling along +x directionDwave travelling along-x direction
Let y=Asin(ωt−kx) represent the variation of distance y of a particle with time t. Which of the following is not meaningful?
View SolutionA sinusoidal wave is given by y=A sin (kx-ωt). The ratio of its maximum particle velocity to wave velocity is
View SolutionThe displacement of a progressive wave is represented by y=Asin(ωt−kx), where x is distance and t is time. Write the dimensional formula of (i) ω and (ii) k.
View Solutiony(xt)=asin(kx−ωt+ϕ) represents a
View Solution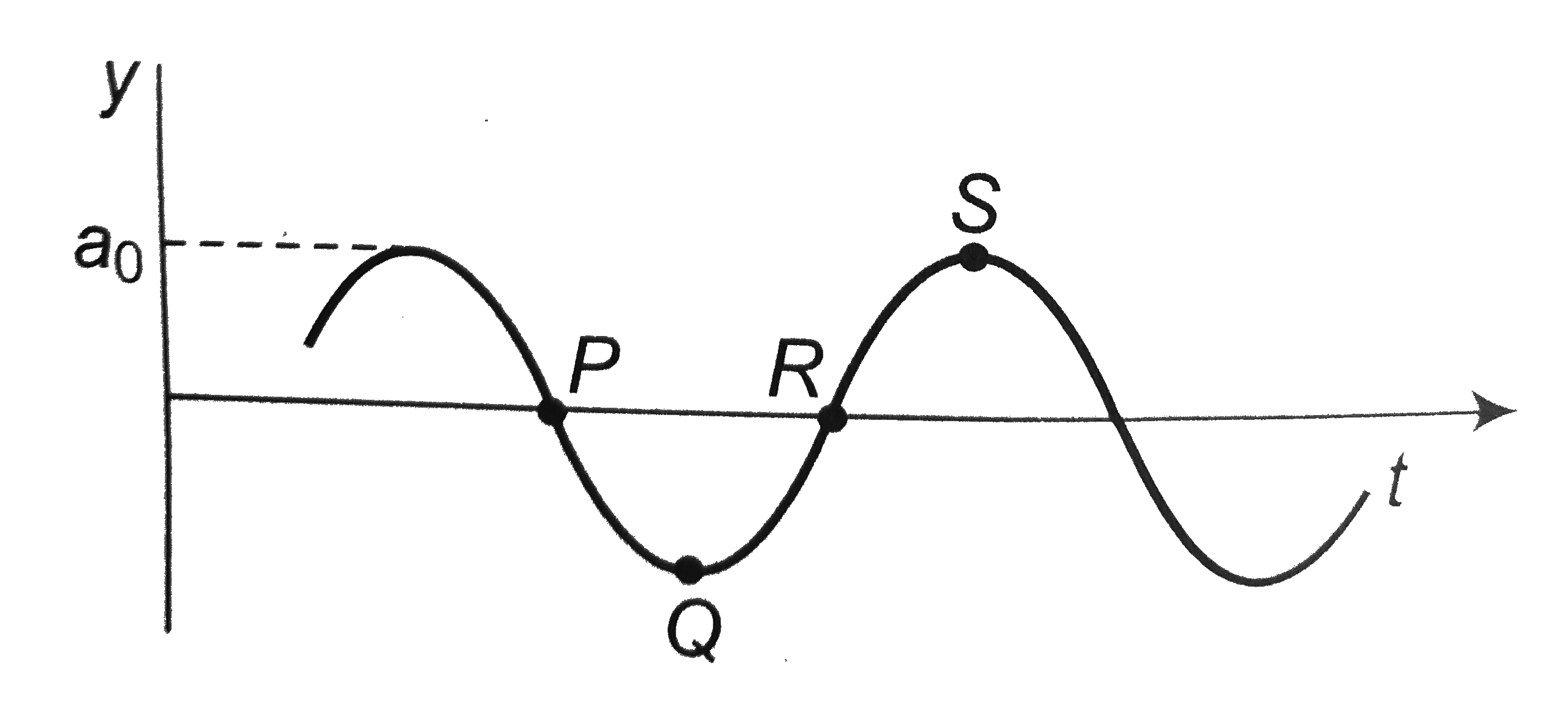
A wave motion has the function y=a0sin(ωt−kx). The graph in figure shows how the displacement y at a fixed point varies with time t. Which one of the labelled points Shows a displacement equal to that at the position x=π2k at time t=0?
View Solution