Let y=Asin(ωt−kx) represent the variation of distance y of a particle with time t. Which of the following is not meaningful?
yA+ω
yω+Atkx
A-kx
A+ωk
The correct Answer is:1,3,4
To determine which of the given options is not meaningful in the context of the expression y=Asin(ωt−kx), we need to analyze the dimensions of each option provided.
1. Understanding the Expression:
The expression y=Asin(ωt−kx) describes a wave, where:
- y is the displacement (dimension of length, (L)).
- A is the amplitude (also dimension of length, (L)).
- ω is the angular frequency (dimension (T−1)).
- k is the wave number (dimension (L−1)).
- t is time (dimension (T)).
- x is position (dimension (L)).
2. Analyzing the Dimensions:
The term ωt has dimensions:
(ωt)=(T−1)(T)=(1) (dimensionless)
The term kx has dimensions:
(kx)=(L−1)(L)=(1) (dimensionless)
Since both ωt and kx are dimensionless, their difference ωt−kx is also dimensionless, making the sine function valid.
3. Evaluating Each Option:
- Option A: yA+ω
- Dimensions: (L)(L)+(T−1)=(1)+(T−1)
- This is not meaningful as you cannot add a dimensionless quantity to a quantity with dimension (T−1).
- Option B: yω+Atkx
- Dimensions: (L)(T−1)+(L)(T)(L−1)(L)=(L)(T)+(T)=(L)(T)+(T)
- This is meaningful since both terms can be combined.
- Option C: A−kx
- Dimensions: (L)−(1)=(L)−(1)
- This is not meaningful as you cannot subtract a dimensionless quantity from a quantity with dimension (L).
- Option D: A+ωk
- Dimensions: (L)+(T−1)(L−1)=(L)+(L)(T−1)
- This is not meaningful since you cannot add quantities with different dimensions.
4. Conclusion:
The options that are not meaningful are A, C, and D. However, since the question asks for which is not meaningful among the provided options, we can conclude that:
- Option A is the first option that is clearly not meaningful.
Final Answer:
Option A is not meaningful.
The expression y=Asin(ωt−kx) describes a wave, where:
- y is the displacement (dimension of length, (L)).
- A is the amplitude (also dimension of length, (L)).
- ω is the angular frequency (dimension (T−1)).
- k is the wave number (dimension (L−1)).
- t is time (dimension (T)).
- x is position (dimension (L)).
The term ωt has dimensions:
(ωt)=(T−1)(T)=(1) (dimensionless)
The term kx has dimensions:
(kx)=(L−1)(L)=(1) (dimensionless)
Since both ωt and kx are dimensionless, their difference ωt−kx is also dimensionless, making the sine function valid.
- Option A: yA+ω
- Dimensions: (L)(L)+(T−1)=(1)+(T−1)
- This is not meaningful as you cannot add a dimensionless quantity to a quantity with dimension (T−1).
- Dimensions: (L)(T−1)+(L)(T)(L−1)(L)=(L)(T)+(T)=(L)(T)+(T)
- This is meaningful since both terms can be combined.
- Dimensions: (L)−(1)=(L)−(1)
- This is not meaningful as you cannot subtract a dimensionless quantity from a quantity with dimension (L).
- Dimensions: (L)+(T−1)(L−1)=(L)+(L)(T−1)
- This is not meaningful since you cannot add quantities with different dimensions.
The options that are not meaningful are A, C, and D. However, since the question asks for which is not meaningful among the provided options, we can conclude that:
- Option A is the first option that is clearly not meaningful.
Option A is not meaningful.
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION D (Linked Comprehension)
3 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION E (Assertion-Reason)
11 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION B Objective (One option is correct )
45 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
10 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
Similar Questions
y(xt)=asin(kx−ωt+ϕ) represents a
View Solutionif y=Asin(ωt−kx), then the value of dydx is
View SolutionThe equation y=Asin2(kx−ωt) represents a wave motion with
View Solution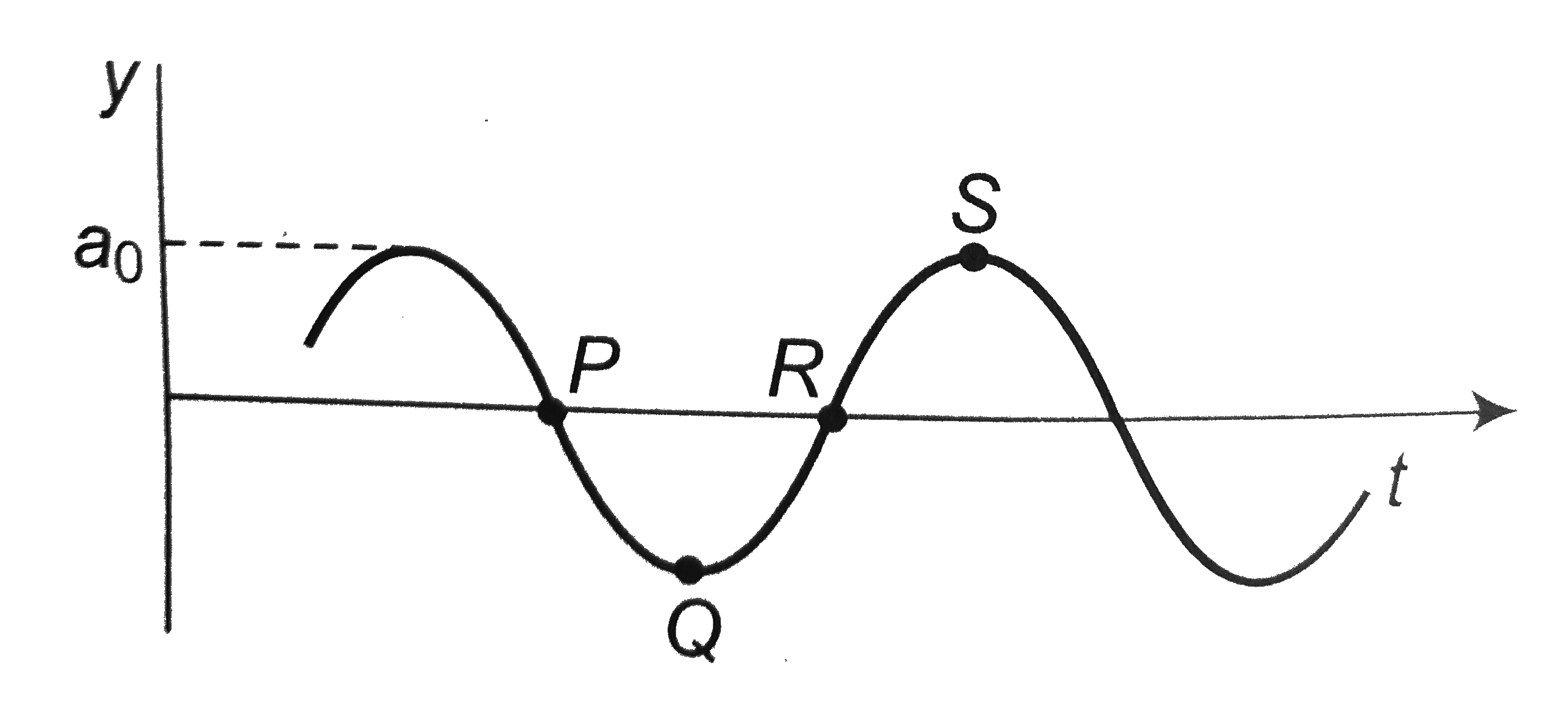
A wave motion has the function y=a0sin(ωt−kx). The graph in figure shows how the displacement y at a fixed point varies with time t. Which one of the labelled points Shows a displacement equal to that at the position x=π2k at time t=0?
View SolutionGiven that y=acos(tP−qx), where t represents distance is metre. Which of the following statements is true ?
View SolutionGiven that y=acos(tP−qx), where t represents distance is metre. Which of the following statements is true ?
View SolutionA particle undergoing SHM has the equation x=Asin(2ωt+ϕ) , where x represents the displacement of the particle. The kinetic energy oscillates with time period
View SolutionThe displacement of a progressive wave is represented by y=Asin(ωt−kx), where x is distance and t is time. Write the dimensional formula of (i) ω and (ii) k.
View SolutionIf y=Asin(ωt−kx), then the value of d2ydt2/d2ydx2
View SolutionA progressive wave of frequency 500 Hz is travelling with a velocity of 360 m/s. How far apart are two points 60∘ out of phase ?
(ii)Does the speed of a plane-progressive wave depend on the amplitude ?
(iii)The equation of a progressive wave is represented by Y=Asin2(kx−ωt). Find its amplitude and frequency
(iv)Which of the following equations represents a wave travelling along positive y-axis ? (a)x=5 sin (2y-6t) (b) y=6sin (7x-5t) (c ) y=10 sin (6y) cos (8t)
View Solution
