A string with tension T and mass per unit length is clamped down at x=0 and at x=L. at t=0, the string is at rest and displaced in the y-direction
Q. What is the total energy at t=0?
a.
b.
c.
d.
The correct Answer is:A
To find the total energy of the string at t=0, we can follow these steps:
Step 1: Understand the Initial Conditions
At t=0, the string is at rest and displaced in the y-direction. The displacement is given by:
y(x,0)=2sin(2πxL)+3sin(πxL)
Step 2: Calculate the Potential Energy Density
The potential energy density dUdx for a string under tension T is given by:
dUdx=12T(∂y∂x)2
Step 3: Find the Derivative of Displacement
We need to compute ∂y∂x:
∂y∂x=∂∂x(2sin(2πxL)+3sin(πxL))
Using the chain rule:
∂y∂x=2⋅2πLcos(2πxL)+3⋅πLcos(πxL)
=4πLcos(2πxL)+3πLcos(πxL)
Step 4: Compute the Square of the Derivative
Now, we square the derivative:
(∂y∂x)2=(4πLcos(2πxL)+3πLcos(πxL))2
Step 5: Expand the Square
Using the identity (a+b)2=a2+2ab+b2:
=(4πLcos(2πxL))2+2(4πLcos(2πxL))(3πLcos(πxL))+(3πLcos(πxL))2
=16π2L2cos2(2πxL)+24π2L2cos(2πxL)cos(πxL)+9π2L2cos2(πxL)
Step 6: Integrate to Find Total Energy
The total energy E is given by integrating the potential energy density over the length of the string:
E=∫L012T(∂y∂x)2dx
Substituting in the expression we derived:
E=12T∫L0(16π2L2cos2(2πxL)+24π2L2cos(2πxL)cos(πxL)+9π2L2cos2(πxL))dx
Step 7: Solve the Integrals
Using the identities for the integrals of cosine squared:
∫L0cos2(nπxL)dx=L2
and
∫L0cos(2πxL)cos(πxL)dx=0 (orthogonality)
we can compute:
E=12T(16π2L2⋅L2+0+9π2L2⋅L2)
=12T(8π2L+9π22L)
=12T⋅25π24L
=25Tπ28L
Final Answer
The total energy at t=0 is:
E=25Tπ28L
At t=0, the string is at rest and displaced in the y-direction. The displacement is given by:
y(x,0)=2sin(2πxL)+3sin(πxL)
The potential energy density dUdx for a string under tension T is given by:
dUdx=12T(∂y∂x)2
We need to compute ∂y∂x:
∂y∂x=∂∂x(2sin(2πxL)+3sin(πxL))
∂y∂x=2⋅2πLcos(2πxL)+3⋅πLcos(πxL)
=4πLcos(2πxL)+3πLcos(πxL)
Now, we square the derivative:
(∂y∂x)2=(4πLcos(2πxL)+3πLcos(πxL))2
Using the identity (a+b)2=a2+2ab+b2:
=(4πLcos(2πxL))2+2(4πLcos(2πxL))(3πLcos(πxL))+(3πLcos(πxL))2
=16π2L2cos2(2πxL)+24π2L2cos(2πxL)cos(πxL)+9π2L2cos2(πxL)
The total energy E is given by integrating the potential energy density over the length of the string:
E=∫L012T(∂y∂x)2dx
E=12T∫L0(16π2L2cos2(2πxL)+24π2L2cos(2πxL)cos(πxL)+9π2L2cos2(πxL))dx
Using the identities for the integrals of cosine squared:
∫L0cos2(nπxL)dx=L2
and
∫L0cos(2πxL)cos(πxL)dx=0 (orthogonality)
we can compute:
E=12T(16π2L2⋅L2+0+9π2L2⋅L2)
=12T(8π2L+9π22L)
=12T⋅25π24L
=25Tπ28L
The total energy at t=0 is:
E=25Tπ28L
Topper's Solved these Questions
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - EXERCISE
20 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-A ( Objective type Questions ))
50 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - Assignment (Section-J) (Subjective Type Questions)
5 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
13 Videos
Similar Questions
A string of mass per unit length μ is clamped at both ends such that one end of the string is at x=0 and the other is at x=L. When string vibrates in fundamental mode, amplitude of the midpoint of string is a and tension in the string is F. Find the total oscillation energy (in J) stored in the string. (Use L=1 m, F = 10N, a = 1/pi m).

View SolutionA 100Hz sinusoidal wave is travelling in the posotive x-direction along a string with a linear mass density of 3.5×10−3kg/m and a tension of 35N. At time t=0, the point x=0 , has maximum displacement in the positive y-direction. Next when this point has zero displacement, the slope of the string is π/20. Which of the following expression represent (s) the displacement of string as a function of x(in metre) and t (in second)
View SolutionA uniform string is clamped at x=0 and x = L and is vibrating in its fundamental mode. Mass per unit length of the string is μ, tension in it is T and the maximum displacement of its midpoint is A. Find the total energy stored in the string. Assume to be small so that changes in tension and length of the string can be ignored
View SolutionString-1 is connected with string-2. The mass per unit length in string-1 is μ1 and the mass per unit length in string-2 is 4μ1. The tension in the strings is T. A travelling wave is coming from the left. What fraction of the energy in the incident wave goes into string-2 ?

View SolutionA rope, under tension of 200N and fixed at both ends, oscialltes in a second harmonic standing wave pattern. The displacement of the rope is given by y=(0.10)sin(πx3)sin(12πt), where x=0 at one end of the rope, x is in metres and t is in seconds. Find the length of the rope in metres.
View SolutionThe velocity of transverse wave in a string is v=√T/m where T is the tension in the string and m is the mass per unit length . If T=3.0kgf, the mass of string is 25g and length of the string isv=1.000m, then the percentage error in the measurement of velocity is
View SolutionA string tied between x=0andx=l vibrates in fundamental mode. The amplitude A, tension T and mass per unit length μ is given. Find the total energy of the string.

View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionThe paritcle displacement (in cm) in a stationary wave is given by y(x,t)=2sin(0.1πx)cos(100πt). The distance between a node and the next antinode is
View SolutionA musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length
μ,2μ,3μand4μ respectively. The instrument is played by vibrating the strings by varying the free length in between the range
L0and2L0. It is found that in string-1
(μ) at free length L0 and tension T0 the fundamental mode frequency is f0 .
List-I gives the above four strings while list-II lists the magnitude of some quantity.
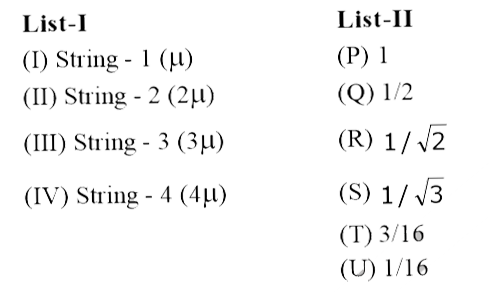
If the tension in each string is T0, the correct match for the highest fundamental frequency in f0 units will be -
View Solution
