Two moles of an ideal gas are contained in a vertical cylinder with a frictionless piston. The piston is slowly displaced so that expansionin gas is isothermal at temperature T0=400K. find the amount of work done in increasing the volume to 3 times.t ake atmospheric pressure =105N/m2
To solve the problem of finding the work done during the isothermal expansion of an ideal gas, we can follow these steps:
Step 1: Understanding the Given Data
We are given:
- Number of moles of gas, n=2 moles
- Initial temperature, T0=400 K
- Initial pressure, P=105 N/m²
- The volume is increased to 3 times its initial volume, i.e., Vf=3Vi
Step 2: Work Done in Isothermal Process
For an isothermal process involving an ideal gas, the work done W can be calculated using the formula:
W=nRTln(VfVi)
Where:
- R is the universal gas constant, approximately 8.314J/(mol K)
- T is the absolute temperature in Kelvin
- Vf is the final volume
- Vi is the initial volume
Step 3: Substituting the Values
In our case:
- Vf=3Vi
- Therefore, VfVi=3
Now substituting the values into the work done formula:
W=nRT0ln(3)
Substituting n=2, R=8.314J/(mol K), and T0=400K:
W=2×8.314×400×ln(3)
Step 4: Calculating the Work Done
Now we need to calculate ln(3):
ln(3)≈1.0986
Now substituting this value:
W=2×8.314×400×1.0986
Calculating this step-by-step:
1. Calculate 2×8.314=16.628
2. Calculate 16.628×400=6651.2
3. Finally, calculate 6651.2×1.0986≈7316.6J
Thus, the work done during the isothermal expansion is approximately:
W≈7316.6J
Final Answer
The amount of work done in increasing the volume to 3 times is approximately 7316.6J.
---
We are given:
- Number of moles of gas, n=2 moles
- Initial temperature, T0=400 K
- Initial pressure, P=105 N/m²
- The volume is increased to 3 times its initial volume, i.e., Vf=3Vi
For an isothermal process involving an ideal gas, the work done W can be calculated using the formula:
W=nRTln(VfVi)
Where:
- R is the universal gas constant, approximately 8.314J/(mol K)
- T is the absolute temperature in Kelvin
- Vf is the final volume
- Vi is the initial volume
In our case:
- Vf=3Vi
- Therefore, VfVi=3
W=nRT0ln(3)
Substituting n=2, R=8.314J/(mol K), and T0=400K:
W=2×8.314×400×ln(3)
Now we need to calculate ln(3):
ln(3)≈1.0986
Now substituting this value:
W=2×8.314×400×1.0986
Calculating this step-by-step:
1. Calculate 2×8.314=16.628
2. Calculate 16.628×400=6651.2
3. Finally, calculate 6651.2×1.0986≈7316.6J
W≈7316.6J
The amount of work done in increasing the volume to 3 times is approximately 7316.6J.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-J) Aakash Challengers Questions
6 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - TRY YOURSELF
12 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-H) Multiple True-False Type Question
2 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-J) Akash Challengers Questions
7 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
Two moles of an ideal gas is contained in a cylinder fitted with a frictionless movable piston, exposed to the atmosphere, at an initial temperature T0. The gas is slowly heated so that its volume becomes four times the initial value. The work done by gas is
View Solution3 moles of an ideal gas are contained within a cylinder by a frictionless piston and are initially at temperature T . The pressure of the gas remains constant while it is heated and its volume doubles . If R is molar gas constant , the work done by the gas in increasing its volume is
View Solution
Knowledge Check
A monatomic ideal gas, initially at temperature T1 is enclosed in a cylinder fitted with a frictionless pistion. The gas is allowed to expand adiabatically to a temperature T2. By releasing the piston suddenly. IF L1 and L2 are th lengths of the gas column before and after expansion respectively, then T1/T2 is given by
A(L1/L2)2/3B(L1/L2)C(L2/L1)D(L2/L1)
An ideal gas has a volume 0.3m3 at 150kPa. It is confined by a spring-loaded piston in a vertical cylinder. Initially, the spring is in relaxed state. If the gas is heated to a final state of 0.5m3 and pressure 600kPa find the work done on the spring (atmospheric pressure, P0=1×105N/m2).

View SolutionTwo moles of nitrogen gas is kept in a cylinder of cross-section area 10cm3. The cylinder is closed by a light frictionless piston. Now the gas is slowly heated such that the displacement of piston during process is 50cm, find the rise in temperature of gas when 200J of heat is added in it. (Atmospheric pressure =100kPa,R=25/3J/mol−K)
View SolutionOne mole of an ideal gas undergoes a process T = 300 + 2V. Then amount of work done by gas when volume increases from 2m3 to 4m3:
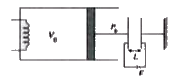
View SolutionAn ideal gas is enclosed in a cylinder fitted with a frictionless piston. The piston is connected with a light rod to one plate of capacitor whose other plate is fixed as shown. Initially volume of the gas inside the cylinder is V0 Atmospheric pressure is P0 separation between the plates is L, area of the piston as well as of the capacitor plates is A and emf of battery is ε . A heater supplies heat to the gas so that pressure of the gas is given as P=P0−nε0ε2L2 when piston is displaced by a distance L2 . Find value of n.
View SolutionTwo moles of a diatomic gas at 300 K are kept in a nonconducting container enclosed by a piston . Gas is now compressed to increase the temperature from 300 K to 400 K. Find word done by the gas

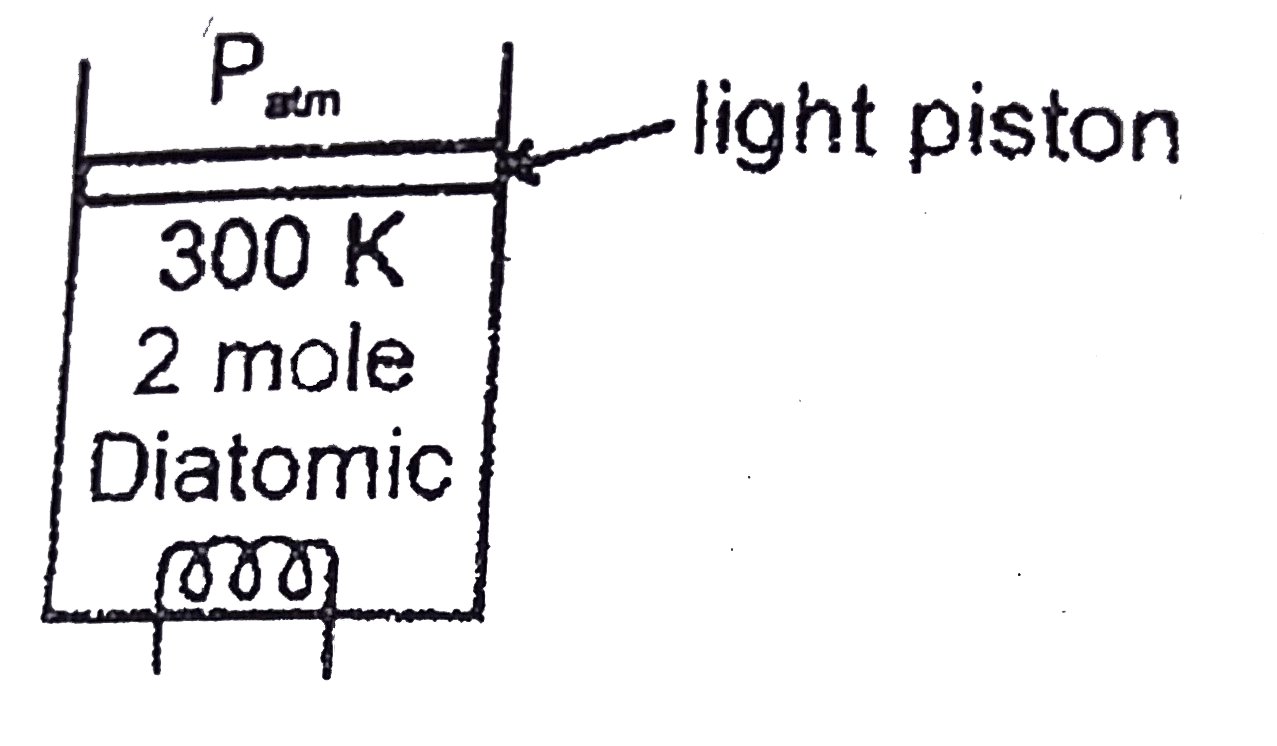
View SolutionTwo moles of a diatomic gas at 300K are enclosed in a cylinder as shown in figure. Piston is light. Find out the heat given if the gas is slowly heated to 400K in the following three cases.
(i) Piston to free to move
(ii) If piston does not move
(iii) If piston is heavy and movable
View Solutionn moles of an ideal gas undergo a process in which the temperature changes with volume as T=kv2. The work done by the gas as the temperature changes from T0 to 4T0 is
View Solution
