A charge q enters into a magnetic field (B) perpendicularly with velocity V. The time rate of work done by the magnetic force on the charge is
qB
None of these
The correct Answer is:D
To solve the problem, we need to analyze the situation where a charge q enters a magnetic field B perpendicularly with a velocity V. We want to determine the time rate of work done by the magnetic force on the charge.
1. Understanding the Motion of the Charge:
When a charged particle enters a magnetic field perpendicularly, it experiences a magnetic force that acts as a centripetal force, causing it to move in a circular path.
2. Magnetic Force Calculation:
The magnetic force F acting on the charge is given by:
F=qVB
where q is the charge, V is the velocity, and B is the magnetic field strength.
3. Centripetal Force:
For circular motion, the centripetal force Fc required to keep the charge moving in a circle is given by:
Fc=mV2R
where m is the mass of the charge and R is the radius of the circular path.
4. Equating Forces:
Since the magnetic force provides the necessary centripetal force, we can equate the two:
qVB=mV2R
5. Finding the Radius:
Rearranging the equation gives us the radius R of the circular path:
R=mVqB
6. Work Done by the Magnetic Force:
The work done W by a force is defined as the product of the force and the displacement in the direction of the force:
W=F⋅d
However, in this case, the magnetic force is always perpendicular to the velocity of the charge. Since the displacement in the direction of the force is zero (the force does not do work on the charge), the work done is:
W=0
7. Rate of Work Done:
The rate of work done (power) is given by:
P=Wt
Since W=0, we have:
P=0t=0
Conclusion:
The time rate of work done by the magnetic force on the charge is zero.
When a charged particle enters a magnetic field perpendicularly, it experiences a magnetic force that acts as a centripetal force, causing it to move in a circular path.
The magnetic force F acting on the charge is given by:
F=qVB
where q is the charge, V is the velocity, and B is the magnetic field strength.
For circular motion, the centripetal force Fc required to keep the charge moving in a circle is given by:
Fc=mV2R
where m is the mass of the charge and R is the radius of the circular path.
Since the magnetic force provides the necessary centripetal force, we can equate the two:
qVB=mV2R
Rearranging the equation gives us the radius R of the circular path:
R=mVqB
The work done W by a force is defined as the product of the force and the displacement in the direction of the force:
W=F⋅d
However, in this case, the magnetic force is always perpendicular to the velocity of the charge. Since the displacement in the direction of the force is zero (the force does not do work on the charge), the work done is:
W=0
The rate of work done (power) is given by:
P=Wt
Since W=0, we have:
P=0t=0
The time rate of work done by the magnetic force on the charge is zero.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section C (Objective Type Questions (More than one option are correct)
14 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section D (Linked Comprehension Type Questions)
10 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment (Section A) Objective Type Questions (One option is correct)
55 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
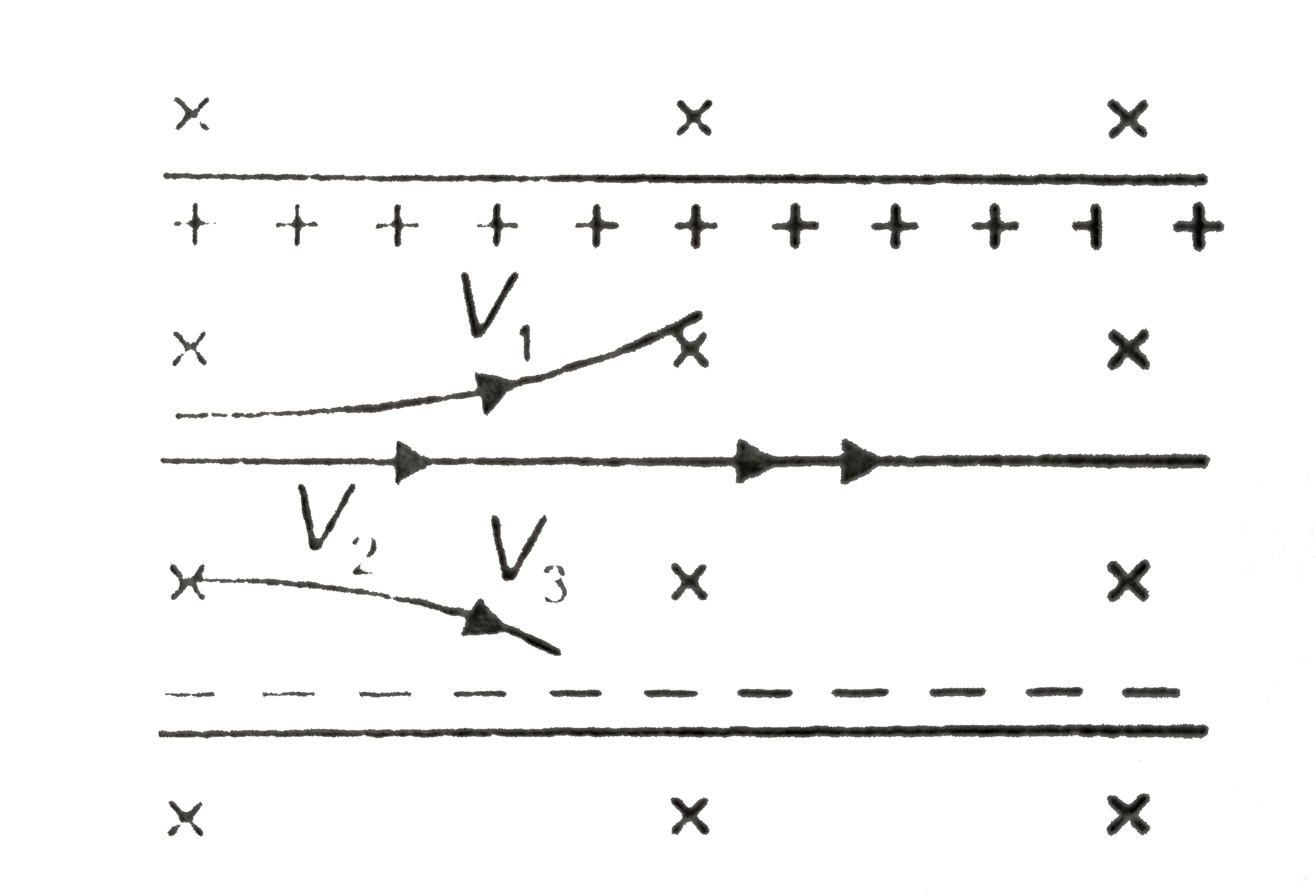
In a region of crossed fields as shown, the strength of electric field is E and that of magnetic field is B. Three positively charged particles with speeds V1,V2andV3 are projected and their paths are shown. From this it implies that
View SolutionThe cyclotron is a device which is used to accelerate charged particles such as protons, deutrons, alpha particles, etc. to very high energy. The principle on which a cyclotron works is based on the fact that an electric field can accelerate a charged particle and a magnetic field can throw it into a circular orbit. A particle of charge +q experiences a force qE in an electric field E and this force is independent of velocity of the particle. The particle is accelerated in the direction of the magnetic field. On the other hand, a magnetic field at right angles to the direction of motion of the particle throws the particle in a circular orbit in which the particle revolves with a frequency that does not depend on its speed. A modest potential difference is used as a sources of electric field. If a charged particle is made to pass through this potential difference a number of times, it will acquire an enormous by large velocity and hence kinetic energy.
Which of the following cannot be accelerated in a cyclotron?
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
View SolutionThe magnetic field produced around a straight line wire when current flows through it is
View SolutionA : Uncertainty principle demands that an electron confined to a nucleus must have very high energy so that the electron cannot reside in a nucleus.
R: The electrostatic attraction between electron and proton is large at such a small distance but is not enough to bind such a high -energy electron.
View SolutionA particle of mass m and charge q enters a magnetic field B perpendicularly with a velocity v , The radius of the circular path described by it will be
View Solutionएक धन आवेशित कण +q किसी समरूप चुंबकीय क्षेत्र B में वेग v क्षेत्र के लंबवत प्रवेश करता है। (i) आवेश पर लगने वाले बल F का सूत्र लिखिए (ii) बल द्वारा किये गए कार्य की गणना कीजिए ।
View SolutionA charge q enters into a magnetic field (B) perpendicularly with velocity V. The time rate of work done by the magnetic force on the charge is
View Solutionएक आवेश q चुम्बकीय क्षेत्र के लम्बवत दिशा में वेग से प्रवेश करता है। इस आवेश पर बल का मान क्या होगा तथा कण का पथ कैसा होगा?
View Solutionचुम्बकीय क्षेत्र→B में वेग →v से गति करते हुए आवेश q के किसी कण पर लगने वाले लॉरेंज बल के लिए व्यंजक लिखिए। प्रदर्शित कीजिए कि इस बल द्वारा आवेशित कण पर कोई कार्य नहीं किया जाता है।
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find impulse of magnetic force.
View Solutionएक आवेश प्रारम्भ वेग v से एक चुम्बकीय क्षेत्र B में प्रवेश करता है चुम्बकीय क्षेत्र B के साथ का 45∘ कोण बनाते हुए प्रविष्ट आवेशित कण का पथ होगा|
View Solutionयदि q कूलाम का आवेशित कण ,V वेग से किसी चुंबकीय क्षेत्र B में गतिशील है तब विद्युत क्षेत्र की अनुपस्थिति में आवेशित कण आरोपित चुंबकीय बल निम्न में से है ?
View Solutionद्रव्यमान m तथा आवेश q का एक कण एक चुम्बकीय क्षेत्र B में v वेग से लम्बवत रूप से प्रवेश करता है इसके द्वारा बने वृत्ताकार पथ की त्रिज्या होगी
View Solutionकथन :- गतिशील आवेश पर चुम्बकीय क्षेत्र द्वारा किया गया कार्य शून्य होता है।
कारण:- चुम्बकीय क्षेत्र मे गतिशील आवेश पर शून्य बल लग सकता है।
View SolutionForce experienced by charge 'q' moving with velocity 'v' in a magnetic field 'B' is given by F = q v B. Find the dimensions of magnetic field.
View Solution
