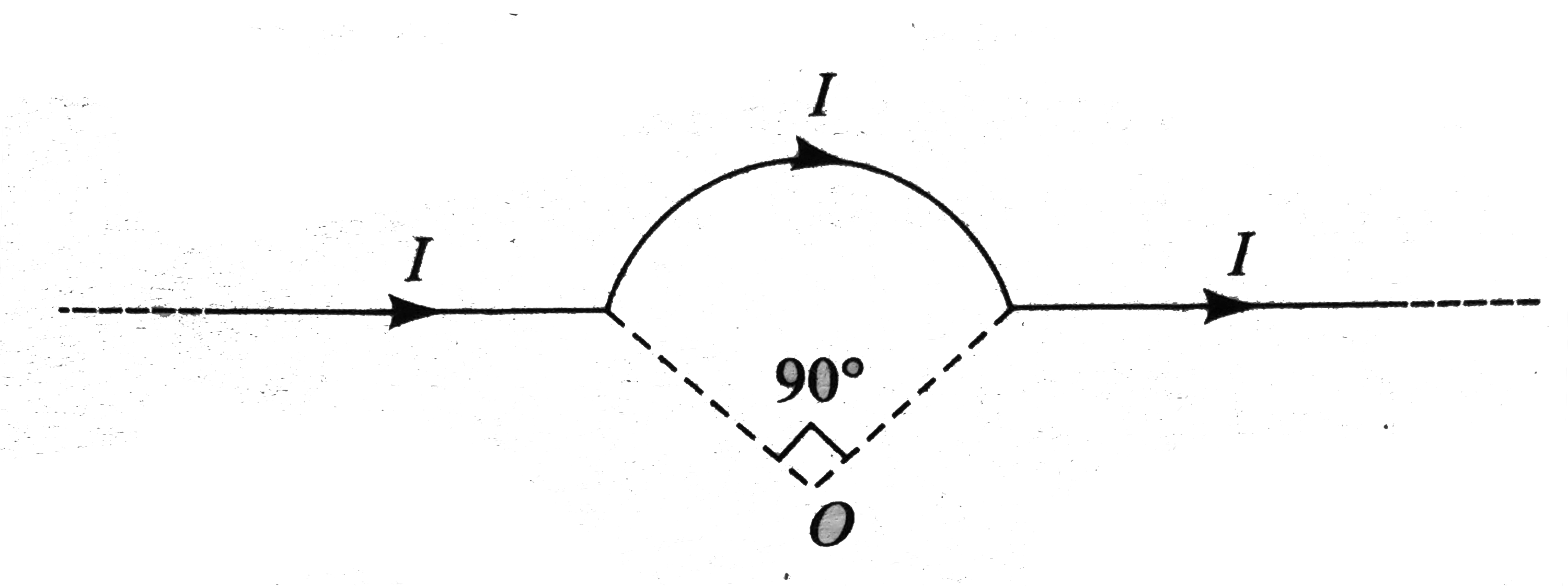
Keeping current per unit length of arc constant, the variation of magnetic field at the centre of an arc (B) with the angle subtended by the arc at the centre (θ) can be best represented by
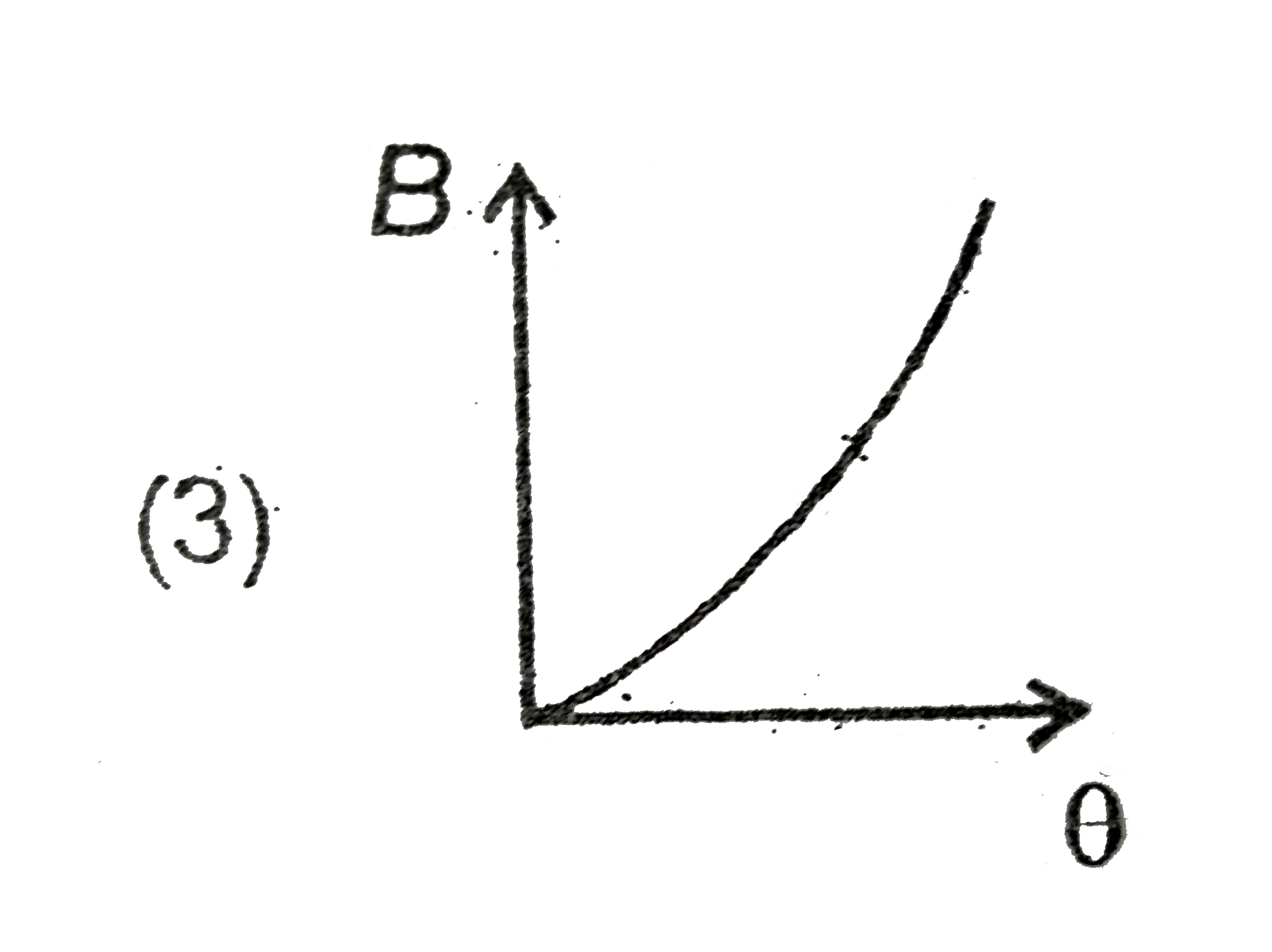

The correct Answer is:C
To solve the problem of how the magnetic field B at the center of an arc varies with the angle θ subtended by the arc at the center, we can follow these steps:
1. Understand the Formula for Magnetic Field:
The magnetic field B at the center of an arc is given by the formula:
B=μ0I2r⋅θ2π
where:
- μ0 is the permeability of free space,
- I is the current flowing through the arc,
- r is the radius of the arc,
- θ is the angle subtended by the arc at the center.
2. Relate Current to Arc Length:
The length L of the arc can be expressed as:
L=rθ
Given that the current per unit length of the arc is constant, we can denote this constant as k. Thus, we have:
IL=k⟹I=kL=k(rθ)
3. Substitute Current into the Magnetic Field Formula:
Now, substitute I=k(rθ) into the magnetic field formula:
B=μ0(krθ)2r⋅θ2π
4. Simplify the Expression:
Simplifying the expression:
B=μ0kθ2⋅θ2π=μ0kθ24π
5. Identify the Relationship:
From the final expression, we see that:
B∝θ2
This indicates that the magnetic field B varies with the square of the angle θ, which is a parabolic relationship.
6. Conclusion:
Therefore, the variation of the magnetic field B at the center of the arc with the angle θ can be best represented as a parabolic function.
Final Answer:
The correct option is that B varies as θ2, which corresponds to a parabolic function.
---
The magnetic field B at the center of an arc is given by the formula:
B=μ0I2r⋅θ2π
where:
- μ0 is the permeability of free space,
- I is the current flowing through the arc,
- r is the radius of the arc,
- θ is the angle subtended by the arc at the center.
The length L of the arc can be expressed as:
L=rθ
Given that the current per unit length of the arc is constant, we can denote this constant as k. Thus, we have:
IL=k⟹I=kL=k(rθ)
Now, substitute I=k(rθ) into the magnetic field formula:
B=μ0(krθ)2r⋅θ2π
Simplifying the expression:
B=μ0kθ2⋅θ2π=μ0kθ24π
From the final expression, we see that:
B∝θ2
This indicates that the magnetic field B varies with the square of the angle θ, which is a parabolic relationship.
Therefore, the variation of the magnetic field B at the center of the arc with the angle θ can be best represented as a parabolic function.
The correct option is that B varies as θ2, which corresponds to a parabolic function.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section C (Objective Type Questions (More than one option are correct)
14 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section D (Linked Comprehension Type Questions)
10 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment (Section A) Objective Type Questions (One option is correct)
55 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Knowledge Check
The angle subtended by an arc of length 20 cm at the centre of circle when radius is 14 cm is
A57 radiansB107 radiansC514 radiansD710 radians
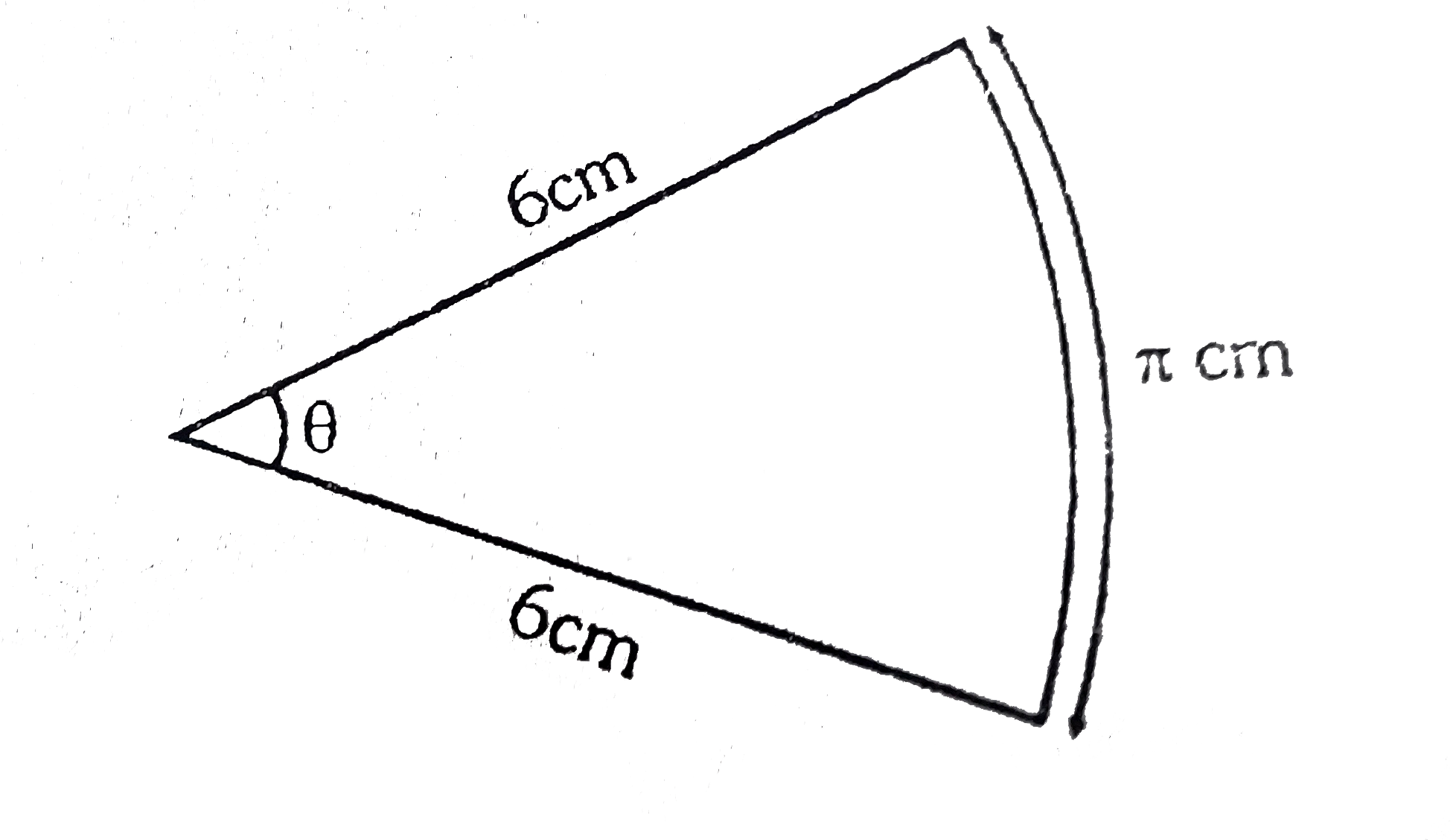
A circular arc of length π cm. Find angle subtended by it at the centre in radian and degree.
View SolutionFind the length of an arc of a circle of 3 cm radius if the angle subtended at the centre is 30∘.(π=3.14).
View SolutionFind, in terms of π , the length of the arc that subtends an angle of 30o at the centre of a circle of radius 4 cm.
View SolutionThe radius of a circle is 50 cm. Find the angle subtends by an arc of 22 cm length at the centerof the circle.
View SolutionIn the figure shown, the magnetic induction at the centre of the arc due to the current in portion AB will be

View SolutionFind the length of an arc of circle of radius 6cm subtending an angle of 15∘ at the centre.
View SolutionFind the length of an arc of a circle of radius 10cm subtending an angle of 300 at the centre
View Solution