For an eye kept at a depth h inside water is refractive index μ, and viewed outside, the radius of circle through which the outer objects can be seen will be
h√μ2−1
hμ
h√μ2+1
(√μ2−1μ)h
The correct Answer is:A
To solve the problem of finding the radius of the circle through which outer objects can be seen from an eye kept at a depth h inside water with refractive index μ, we can follow these steps:
1. Understanding the Situation:
- We have an eye located at a depth h in water.
- The refractive index of water is given as μ.
- We need to determine the radius of the circle from which objects can be seen outside the water.
2. Identifying the Critical Angle:
- The critical angle θc is the angle of incidence above which total internal reflection occurs.
- The relationship between the critical angle and the refractive index is given by:
sinθc=1μ
3. Relating the Critical Angle to the Radius:
- At the critical angle, the refracted ray travels along the surface of the water. The geometry of the situation can be analyzed using a right triangle where:
- The height h is the opposite side.
- The radius r is the adjacent side.
- We can use the tangent function:
tanθc=rh
4. Expressing tanθc:
- We know that:
tanθc=sinθccosθc
- From the sine relation, we can find cosθc using the Pythagorean identity:
cosθc=√1−sin2θc=√1−(1μ)2=√μ2−1μ2
5. Substituting into the Tangent Formula:
- Now substituting sinθc and cosθc into the tangent formula:
tanθc=1μ√μ2−1μ2=1μ⋅μ√μ2−1=1√μ2−1
6. Finding the Radius:
- From the tangent relation:
tanθc=rh⟹r=htanθc=h⋅1√μ2−1
- Therefore, the radius r can be expressed as:
r=h√μ2−1
Final Answer:
The radius of the circle through which outer objects can be seen is:
r=h√μ2−1
- We have an eye located at a depth h in water.
- The refractive index of water is given as μ.
- We need to determine the radius of the circle from which objects can be seen outside the water.
- The critical angle θc is the angle of incidence above which total internal reflection occurs.
- The relationship between the critical angle and the refractive index is given by:
sinθc=1μ
- At the critical angle, the refracted ray travels along the surface of the water. The geometry of the situation can be analyzed using a right triangle where:
- The height h is the opposite side.
- The radius r is the adjacent side.
- We can use the tangent function:
tanθc=rh
- We know that:
tanθc=sinθccosθc
- From the sine relation, we can find cosθc using the Pythagorean identity:
cosθc=√1−sin2θc=√1−(1μ)2=√μ2−1μ2
- Now substituting sinθc and cosθc into the tangent formula:
tanθc=1μ√μ2−1μ2=1μ⋅μ√μ2−1=1√μ2−1
- From the tangent relation:
tanθc=rh⟹r=htanθc=h⋅1√μ2−1
- Therefore, the radius r can be expressed as:
r=h√μ2−1
The radius of the circle through which outer objects can be seen is:
r=h√μ2−1
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)9videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - D) Linked Comprehension Type Questions12videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)38videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)4videos
PHYSICAL WORLD
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)10videos
SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )
Similar Questions
If we see the outside objects by keeping an eye at a depth h inside water of refractive index u, then the value of RADIUS of circle of view for outside objects will be
View SolutionThere is a small black dot at the centre C of a solid glass sphere of refractive index μ. When seen from outside, the dot will appear to be located
View Solution
Knowledge Check
- Question 1 - Select One
A point source of light is placed at a depth of h below the surface of water of refractive index μ. A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface. The minimum diameter of the disc is
A2h(μ2−1)1/2B2h(μ2−1)1/2Ch2(μ2−1)1/2Dh(μ2−1)1/2 - Question 2 - Select One
A vesse of depth x is half filled with oil of refractive index μ1 and the other half is filled with water of refrative index μ2. The apparent depth of the vessel when viewed above is
Ax(μ1+μ2)2μ1μ2Bxμ1μ22(μ1+μ2)Cxμ1μ2(μ1+μ2)D2x(μ1+μ2)μ1μ2
A concave mirror of radius R is kept on a horizontal table. Water (refractive index =mu.) is poured into it up to a height h. Where should an object be placed so that its image is formed on itself ?
 View Solution
View SolutionA point source is placed at a depth h below the surface of water (refractive index =μ). The medium above the surface area of water is air from water.
View SolutionA point source is placed at a depth h below the surface of water (refractive index = mu). (a) Show that light escapes through a circular area on the water surface with its centre directly above the point source. (b) Find the angle subtended by a radius of the area on the source.
View SolutionObject O is kept in air in fron of a thin plano convex lens of radius of curvature 10cm. It's refractive index is 3/2 and the medium toward right of plane surface is water of refractive indec 4/3 . What should be the distance x of the object so that the rays become parrallel finall?
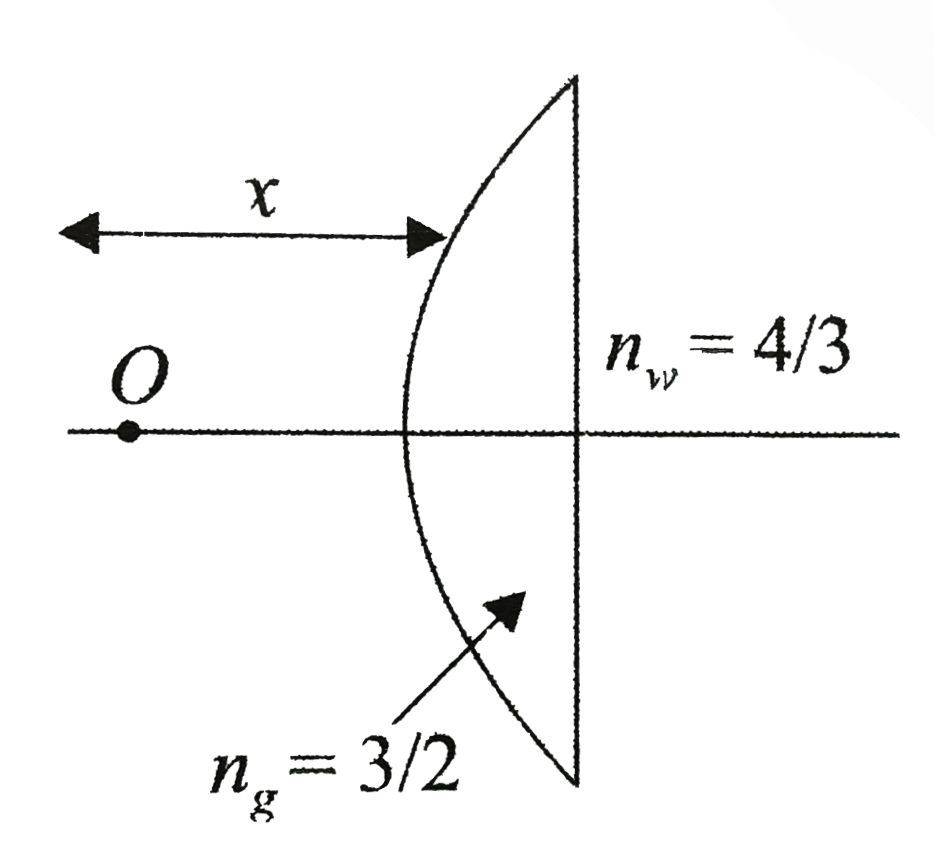 View Solution
View SolutionA cylinder is filled with a liquid of refractive index μ. The radius of the cylinder is decreasing at a constant rate K. The volume of the liquid inside the container remains constant at V. The observer and the object O are in a state of rest at a distance L from each other. When radius of cylinder is r the apparent velocity of the object as seen by the observer is
 View Solution
View SolutionAn object of height 1mm is placed inside a sphere of refractive index μ=2 and radius of curvature 20 cm as shown in the figure. Find the position, size, and nature of image, for the situation shown in Figure. Draw ray diagram.
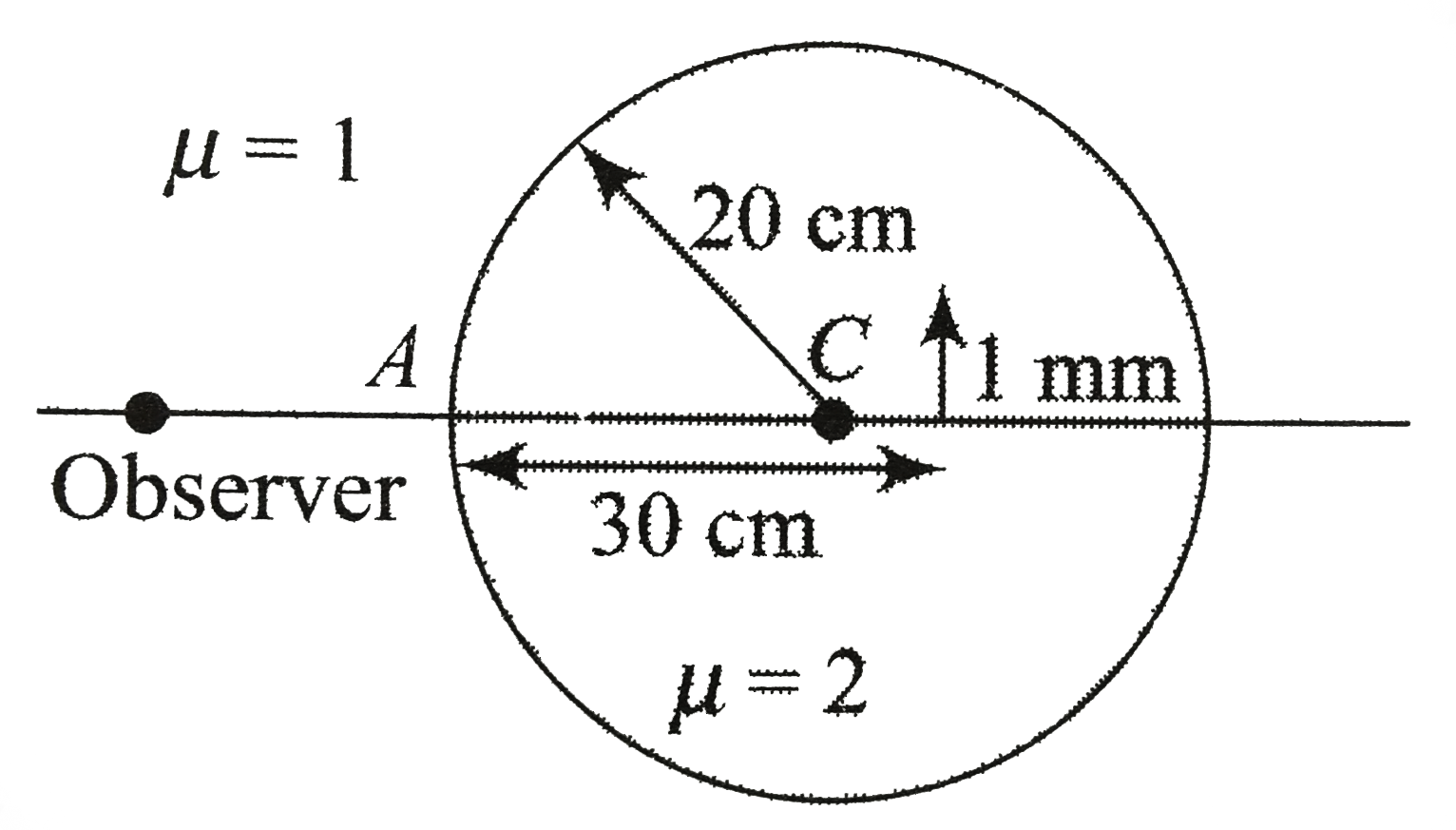 View Solution
View Solution

