A lens forms a sharp image on a screen. On inserting a parallel sided glass slab between the lens and the screen, it is found necessary to move the screen a distance d away the lens in order for the image to be sharp again. If the refractive index of the material of the slab is μ, the thickness of the slab is
μd
dμ
(μ−1)dμ
μdμ−1
The correct Answer is:D
To solve the problem, we need to determine the thickness of the glass slab that causes the screen to be moved a distance d away from the lens to regain a sharp image.
1. Understanding the Setup:
- A lens forms a sharp image on a screen.
- When a parallel-sided glass slab is placed between the lens and the screen, the image shifts, and the screen must be moved to restore the sharp image.
2. Identifying the Shift:
- The distance the screen must be moved to regain focus is given as d.
- The thickness of the glass slab is denoted as t.
- The refractive index of the glass slab is denoted as μ.
3. Using the Formula for Shift:
- When a glass slab is inserted, the effective distance light travels changes due to the refractive index. The formula for the shift in the position of the image caused by the slab is given by:
d=t(1−1μ)
4. Rearranging the Formula:
- We can rearrange the formula to express the thickness t in terms of the distance d and the refractive index μ:
d=t(1−1μ)
- Rearranging gives:
t=d1−1μ=dμμ−1
5. Final Expression for Thickness:
- Thus, the thickness of the slab is:
t=dμμ−1
Conclusion:
The thickness of the glass slab is given by:
t=dμμ−1
- A lens forms a sharp image on a screen.
- When a parallel-sided glass slab is placed between the lens and the screen, the image shifts, and the screen must be moved to restore the sharp image.
- The distance the screen must be moved to regain focus is given as d.
- The thickness of the glass slab is denoted as t.
- The refractive index of the glass slab is denoted as μ.
- When a glass slab is inserted, the effective distance light travels changes due to the refractive index. The formula for the shift in the position of the image caused by the slab is given by:
d=t(1−1μ)
- We can rearrange the formula to express the thickness t in terms of the distance d and the refractive index μ:
d=t(1−1μ)
- Rearranging gives:
t=d1−1μ=dμμ−1
- Thus, the thickness of the slab is:
t=dμμ−1
The thickness of the glass slab is given by:
t=dμμ−1
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)
9 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - D) Linked Comprehension Type Questions
12 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
38 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)
10 Videos
Similar Questions
If final image after two refractions through the lens and one reflection from the mirror forms at the same point O. Refrative index of the material of the lens μ=3/2. Then find d.

View SolutionA lens with a focal length of f=30cm produces on a screen a sharp image of an object that is at a distance of a=40cm from the lens. A plane parallel plate with thickness of d=9cm is placed between the lens and the object perpendicular to the optical axis of the lens. Through what distance should the screen be shifted for the image of the object to remain distinct? The refractive index of the glass of the plate is μ=1.8.
View Solution
Knowledge Check
A converging lens is used to form an image on a screen. When the upper half of the lens is covered by an opaque screen
Ahalf the image will disappearBcomplete image will disappearCintensity of image will decreaseDintensity of image will increase
In a slide show programme, the image on the screen has an area 900times that of the slide. If the distance between the slide and the screen is x times the distance between the slide and the projector lens, then
View SolutionThe distance between an object and the screen is 100cm. A lens produces an image on the screen when the lens is placed at either of the positions 40cm apart. The power of the lens is nearly
View SolutionAn object O is placed in front of a convex lens such that the lens forms a sharp image on the screen. The distance between the object and screen is 10 cm. The lens is made of glass at refractive index μg=32. The surrounding medium is air with refractive index 1.
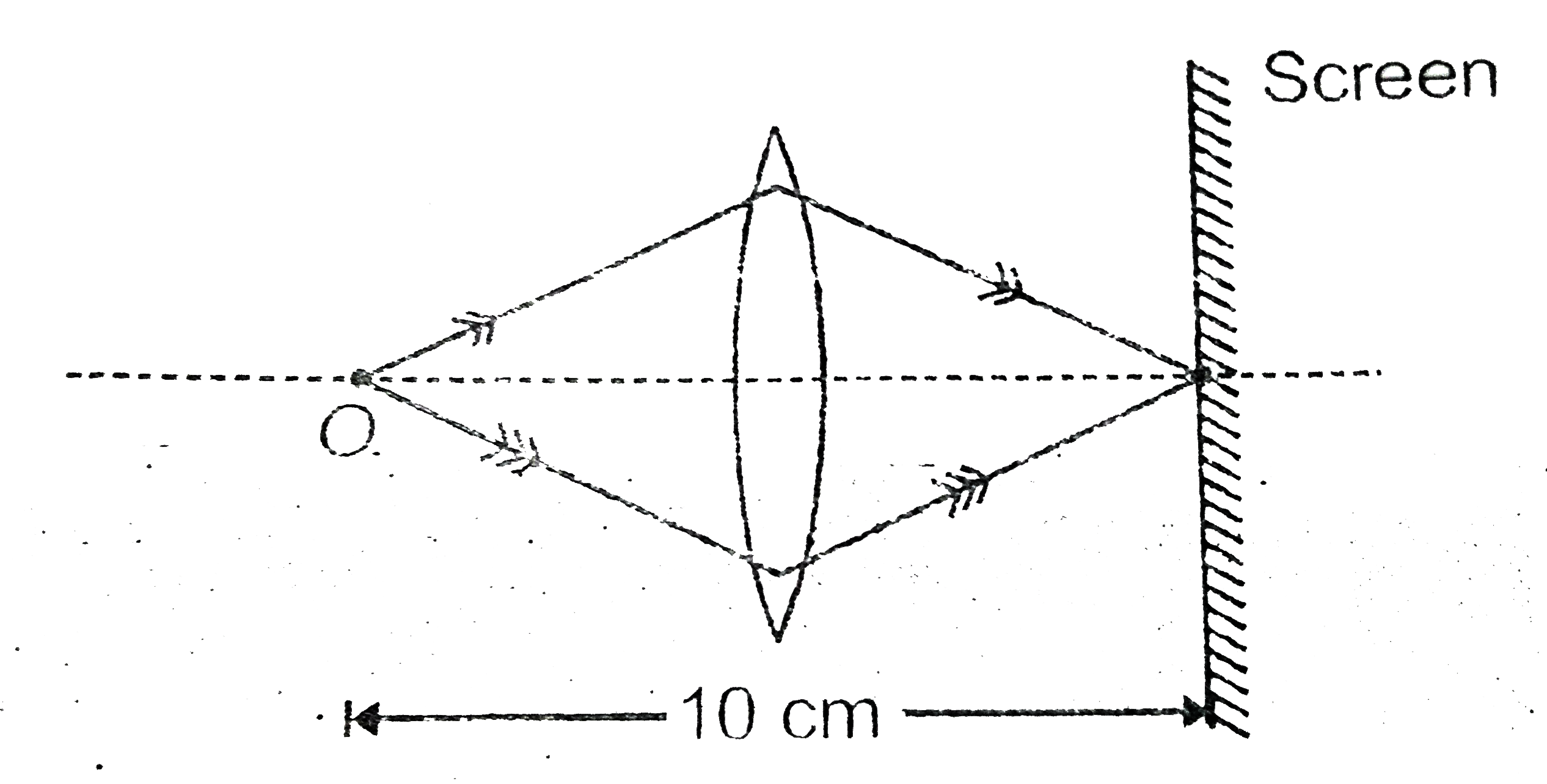
The focal length of the lens, used in the above experiment, satisfies the condition given by
View SolutionAn object O is placed in front of a convex lens such that the lens forms a sharp image on the screen. The distance between the object and screen is 10 cm. The lens is made of glass at refractive index μg=32. The surrounding medium is air with refractive index 1.

The focal length of the lens, used in the above experiment, satisfies the condition given by
View SolutionA converging lens is used to form an image on a screen. When the upper half of the lens is covered by an opaque screen
View SolutionA converging lens is used to form an image on a screen. When the upper half of the lens is covered by an opaque screen
View SolutionA luminous object is separated from a screen by distance d. A convex lends is placed between the object and the screeen such that it forms a distinct image on the screen. The maximum possible focal length of this convex lens is.
View Solution