A parallel incident beam falls on a solid glass sphere at near normal incidence.Show that the image in terms of the index of refractive μ and the sphere of radius R is given by
R(2−μ)2(μ−1)
To solve the problem of finding the image distance for a parallel incident beam falling on a solid glass sphere at near normal incidence, we will use the lens maker's formula and the principles of refraction.
Step 1: Understanding the Setup
- We have a solid glass sphere with radius R and refractive index μ. A parallel beam of light is incident on the sphere near normal incidence.
Hint 1: Draw a diagram of the sphere with the incident rays to visualize the problem.
Step 2: Refraction at the First Surface
- For the first surface of the sphere, we can use the lens maker's formula:
μ2V−μ1U=μ2−μ1R
- Here, μ1=1 (air), μ2=μ (glass), and since the incident rays are parallel, we can take U=∞ (object at infinity).
Hint 2: Remember that for an object at infinity, the image distance V simplifies the equation.
Step 3: Substitute Values
- Substituting the values into the equation:
μV−1∞=μ−1R
- This simplifies to:
μV=μ−1R
- Rearranging gives:
V=Rμμ−1
Hint 3: Keep track of the signs and the relationships between object and image distances.
Step 4: Image Formation at the Second Surface
- The image formed by the first surface acts as an object for the second surface. The distance of this image from the center of the sphere is V1=V−2R (since the center to the first surface is R).
- Substituting V:
V1=Rμμ−1−2R
- Simplifying gives:
V1=R(μ−2(μ−1)μ−1)=R(μ−2μ+2μ−1)=R(2−μμ−1)
Hint 4: Make sure to correctly handle the algebra when combining terms.
Step 5: Refraction at the Second Surface
- Now, we apply the lens maker's formula again for the second surface:
μ2V−μ1U=μ2−μ1R
- Here, U=V1 and μ2=1 (air), μ1=μ:
1V−μV1=1−μ−R
- Rearranging gives:
1V=μV1+μ−1R
Hint 5: Ensure you are consistent with the signs when substituting values into the equation.
Step 6: Substitute V1 and Solve for V
- Substitute V1=R2−μμ−1 into the equation:
1V=μR2−μμ−1+μ−1R
- Simplifying this will yield:
V=R(2−μ)2(μ−1)
Final Result:
- The image distance V in terms of the index of refraction μ and the radius R is given by:
V=R(2−μ)2(μ−1)
- We have a solid glass sphere with radius R and refractive index μ. A parallel beam of light is incident on the sphere near normal incidence.
- For the first surface of the sphere, we can use the lens maker's formula:
μ2V−μ1U=μ2−μ1R
- Here, μ1=1 (air), μ2=μ (glass), and since the incident rays are parallel, we can take U=∞ (object at infinity).
- Substituting the values into the equation:
μV−1∞=μ−1R
- This simplifies to:
μV=μ−1R
- Rearranging gives:
V=Rμμ−1
- The image formed by the first surface acts as an object for the second surface. The distance of this image from the center of the sphere is V1=V−2R (since the center to the first surface is R).
- Substituting V:
V1=Rμμ−1−2R
- Simplifying gives:
V1=R(μ−2(μ−1)μ−1)=R(μ−2μ+2μ−1)=R(2−μμ−1)
- Now, we apply the lens maker's formula again for the second surface:
μ2V−μ1U=μ2−μ1R
- Here, U=V1 and μ2=1 (air), μ1=μ:
1V−μV1=1−μ−R
- Rearranging gives:
1V=μV1+μ−1R
- Substitute V1=R2−μμ−1 into the equation:
1V=μR2−μμ−1+μ−1R
- Simplifying this will yield:
V=R(2−μ)2(μ−1)
- The image distance V in terms of the index of refraction μ and the radius R is given by:
V=R(2−μ)2(μ−1)
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - J) Aakash Challengers Questions
7 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXAMPLE
75 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - H) Multiple True-FalseType Questions
3 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)
10 Videos
Similar Questions
A parallel incident beam falls on a solid glass sphere at normal incidenc. Prove that the distance of the fianll image after two refractions is at a distance (2−μ)/2(μ−1)a from the outer edge of the sphere. Refractive index of the sphere is μ and radius of the sphere is a.
View SolutionA parallel beam of light falls on a solid tranparent sphere.
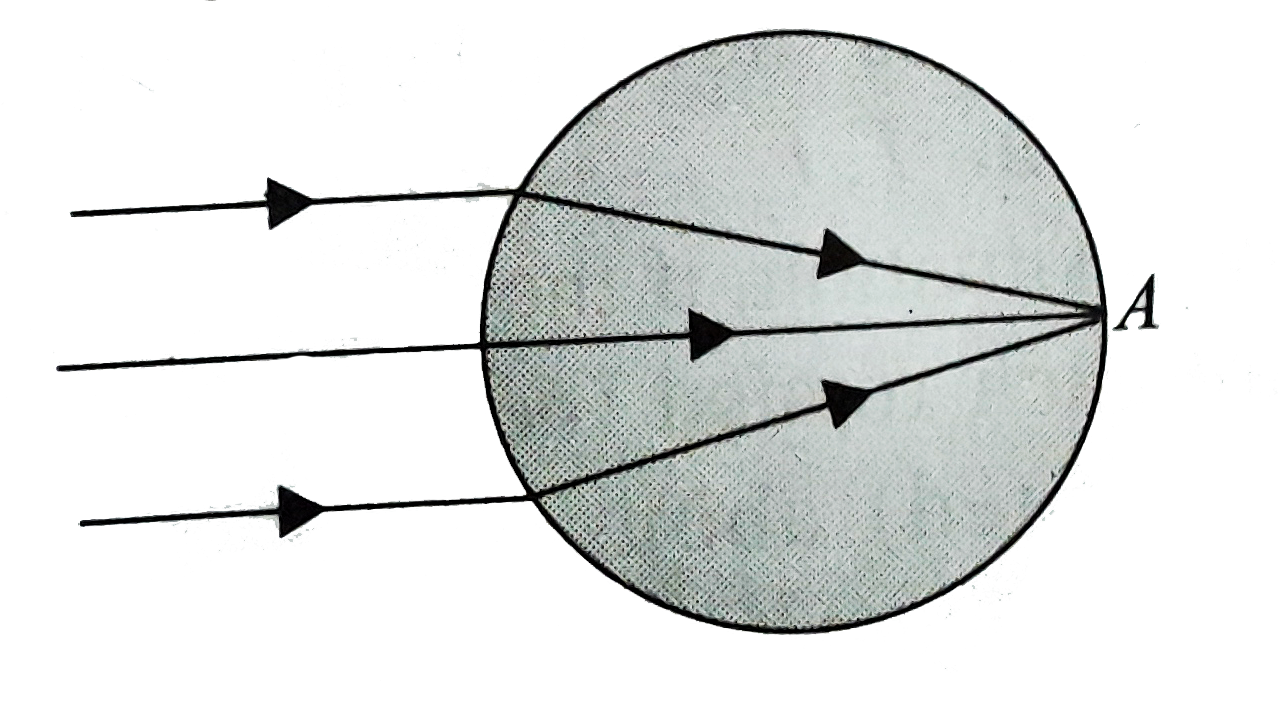
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,
View SolutionA parallel beam of light falls on a solid tranparent sphere.

Q. For what value of refractive index μ, the thin beam can be focussed at centre of sphere.
View SolutionA parallel beam falls on solid glass sphere of radius R and refractive index μ. What is the distance of final image after refractioin from two surfaces of sphere? What is the condition for the image to be real?
View SolutionA light ray is incident on a glass sphere at an angle of incidence 60∘ as shown. Find the angles r,r1,e and the total deviation after two refractions.

View SolutionA ray of light is incident on a glass sphere of refractive index 3/2. What should be the angle of incidence so that the ray which enters the sphere does not come out of the sphere ?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA horizontal ray of light is incident on a solid glass sphere of radius R and refractive index μ . What is net deviation of the beam when it emerged from the other side of the sphere?
View SolutionA ray of light ravels from a liquid of refractive index μ to air. If the incident beam is rotating at a rate ω , what is the angular sped of the refracted beam at the instant the angle of incidence is 30∘ ? (Given μ=√2,ω=1/√6rads−1).
View Solution
