If the work function of a metal is 'ϕ' and the frequency of the incident light is 'v', there is no emission of photoelectron if
v<ϕh
v=ϕh
v>ϕh
v>=<ϕh
The correct Answer is:1
To solve the problem regarding the emission of photoelectrons from a metal when exposed to light of a certain frequency, we can follow these steps:
1. Understand the Concept of Work Function:
The work function (φ) of a metal is the minimum energy required to remove an electron from the surface of that metal.
2. Energy of Incident Light:
The energy (E) of the incident light can be calculated using the formula:
E=h⋅v
where:
- E is the energy of the incident light,
- h is Planck's constant (6.626×10−34Js),
- v is the frequency of the incident light.
3. Condition for Photoelectron Emission:
For photoelectrons to be emitted from the metal, the energy of the incident light must be greater than or equal to the work function of the metal:
E≥ϕ
This means:
h⋅v≥ϕ
4. Condition for No Emission:
If there is no emission of photoelectrons, it implies that the energy of the incident light is less than the work function:
h⋅v<ϕ
5. Rearranging the Inequality:
To express this condition in terms of frequency, we rearrange the inequality:
v<ϕh
6. Conclusion:
Therefore, the condition for no emission of photoelectrons is that the frequency of the incident light must be less than the ratio of the work function to Planck's constant:
v<ϕh
Final Answer:
There is no emission of photoelectrons if:
v<ϕh
The work function (φ) of a metal is the minimum energy required to remove an electron from the surface of that metal.
The energy (E) of the incident light can be calculated using the formula:
E=h⋅v
where:
- E is the energy of the incident light,
- h is Planck's constant (6.626×10−34Js),
- v is the frequency of the incident light.
For photoelectrons to be emitted from the metal, the energy of the incident light must be greater than or equal to the work function of the metal:
E≥ϕ
This means:
h⋅v≥ϕ
If there is no emission of photoelectrons, it implies that the energy of the incident light is less than the work function:
h⋅v<ϕ
To express this condition in terms of frequency, we rearrange the inequality:
v<ϕh
Therefore, the condition for no emission of photoelectrons is that the frequency of the incident light must be less than the ratio of the work function to Planck's constant:
v<ϕh
There is no emission of photoelectrons if:
v<ϕh
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:ASSIGNMENT SECTION B.Objective (Only one answer)
Explore 6 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:ASSIGNMENT SECTION C. Objective (More than one answer)
Explore 4 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:Try Yourself
Explore 41 Videos
- CURRENT ELECTRICITYBook:AAKASH INSTITUTE ENGLISHChapter:CURRENT ELECTRICITYExercise:ASSIGNMENT SECTION-J
Explore 10 Videos
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:comprehension
Explore 3 Videos
Similar Questions
Knowledge Check
The work function of Cs is 2.14 ev find the wavelength of the incident light if the stopping potential is 0.6 V.
A326 nmB454 nmC524 nmD232 nm
Two photons of energies twice and thrice the work function of a metal are incident on the metal surface .Then, the ratio of maximum velocities of the photoelectrons emitted in the two cases respectively ,is
View SolutionCalculate the valocity of a photoelectron if the work function of the target material is 1.24eV and the wavelength of incident light is 4.36×10−7m. What retarding potentia is necessary to stop the emission of the electrons?
View SolutionThe threshold frequency for certain metal is v0. When light of frequency 2v0 is incident on it, the maximum velocity of photoelectrons is 4×106ms−1. If the frequency of incident radiation is increaed to 5v0, then the maximum velocity of photoelectrons will be
View SolutionThreshold frequency for a certain metal is v0. When light of frequency 2v0 is incident on it, the maximum velocity of photoelectrons is 4×108cms−1. If frequency of incident radiation is increased to 5v0, then the maximum velocity of photoelectrons, in cm s−1, will be
View SolutionThe work function of a metal is hv0. Light of frequency v falls on this metal. The photoelectric effect will take place only if
View SolutionThe following figure shows a graph for the stopping potential as a function of the frequency of incident light illuminating a metal surface. Find the photoelectric work function for this surface.
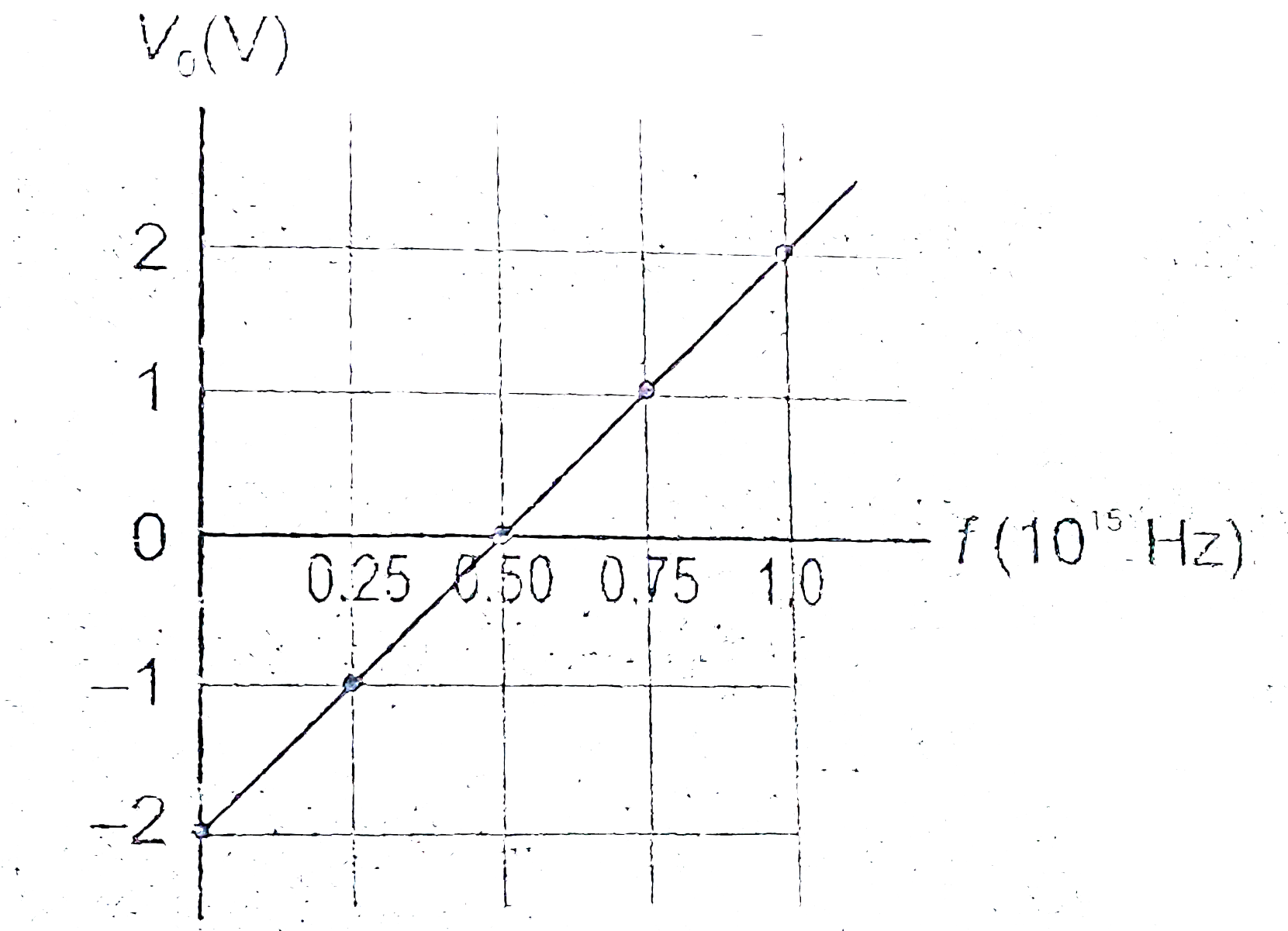
View SolutionThe photoelectric threshold frequency of a metal is v. When light of frequency 4v is incident on the metal . The maximum kinetic energy of the emitted photoelectrons is
View Solution