The addition of three masses 1.6 g, 7.32 g and 4.238 g. addressed upto proper decimal places is
13.158 g
13.2 g
13.16 g
13.15 g
The correct Answer is:2
To solve the problem of adding the three masses (1.6 g, 7.32 g, and 4.238 g) and expressing the result with the correct number of decimal places, we can follow these steps:
Step 1: Add the masses
First, we will add the three given masses together.
\(
1.6 \, \text{g} + 7.32 \, \text{g} + 4.238 \, \text{g}
\)
Step 2: Perform the addition
Align the numbers by their decimal points and add them:
1.600+7.320+4.238−−−−−−−−−13.158
So, the total mass is:
\(
13.158 \, \text{g}
\)
Step 3: Determine the number of decimal places
Next, we need to determine how many decimal places our final answer should have. We look at the original numbers:
- 1.6 g has 1 decimal place.
- 7.32 g has 2 decimal places.
- 4.238 g has 3 decimal places.
The rule for addition is that the result should have the same number of decimal places as the measurement with the least number of decimal places. In this case, that is 1 decimal place (from 1.6 g).
Step 4: Round the result
Now, we round the total (13.158 g) to 1 decimal place.
The first digit after the decimal is 1 (in 13.158). Since the digit after the first decimal place (which is 5) is 5 or greater, we round up the first decimal place:
- The digit before rounding is 1.
- Since the next digit is 5, we round up: 1 becomes 2.
Thus, rounding 13.158 g to 1 decimal place gives us:
\(
13.2 \, \text{g}
\)
Final Answer
The final answer, expressed to the correct number of decimal places, is:
\(
\text{13.2 g}
\)
---
First, we will add the three given masses together.
1.6 \, \text{g} + 7.32 \, \text{g} + 4.238 \, \text{g}
\)
Align the numbers by their decimal points and add them:
13.158 \, \text{g}
\)
Next, we need to determine how many decimal places our final answer should have. We look at the original numbers:
- 7.32 g has 2 decimal places.
- 4.238 g has 3 decimal places.
Now, we round the total (13.158 g) to 1 decimal place.
- Since the next digit is 5, we round up: 1 becomes 2.
13.2 \, \text{g}
\)
The final answer, expressed to the correct number of decimal places, is:
\text{13.2 g}
\)
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION B Objective (One option is correct )
45 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION C Objective (More than one option is correct )
10 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Try Yourself
82 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
10 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
Similar Questions
The mass of a box measured by grocer's balance is 4.2 kg. Two additional masses 10.20 g and 15.25 g are added to the box. What is the total mass of the box?
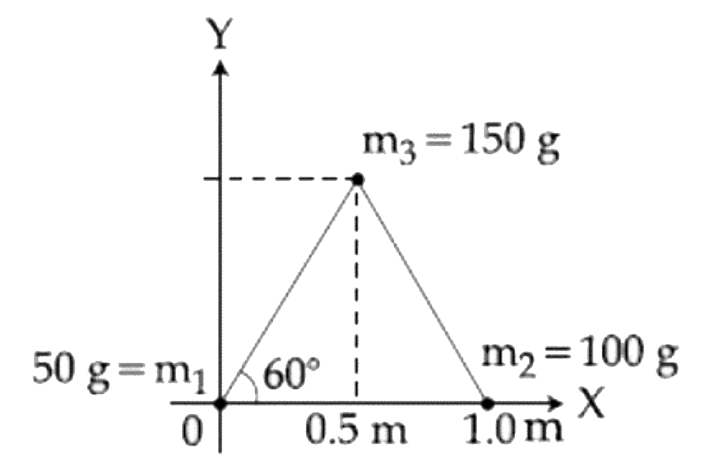
View SolutionThree particles of massses 50 g, 100 g and 150 g are placed at the vertices of an equilateral triangle of side 1m ( as shown in the figure ) . The ( x, y) coordinates of the centre of mass will be :
View SolutionThree particles of masses 1 g, 2g and 3 g are kept at points (2cm,0), (0.6 cm), (4cm, 3cm) find moment of inertia of all three particles (in gm−cm(2)) about (a) x-axis
(b). Y-axis
(c). Z-axis.
View SolutionThe velocities of three particles of masses 20 g, 30 g and 50 g are 10ˆi, 10ˆj and 10ˆk respectively. The velocity of the centre of mass of the three particles is
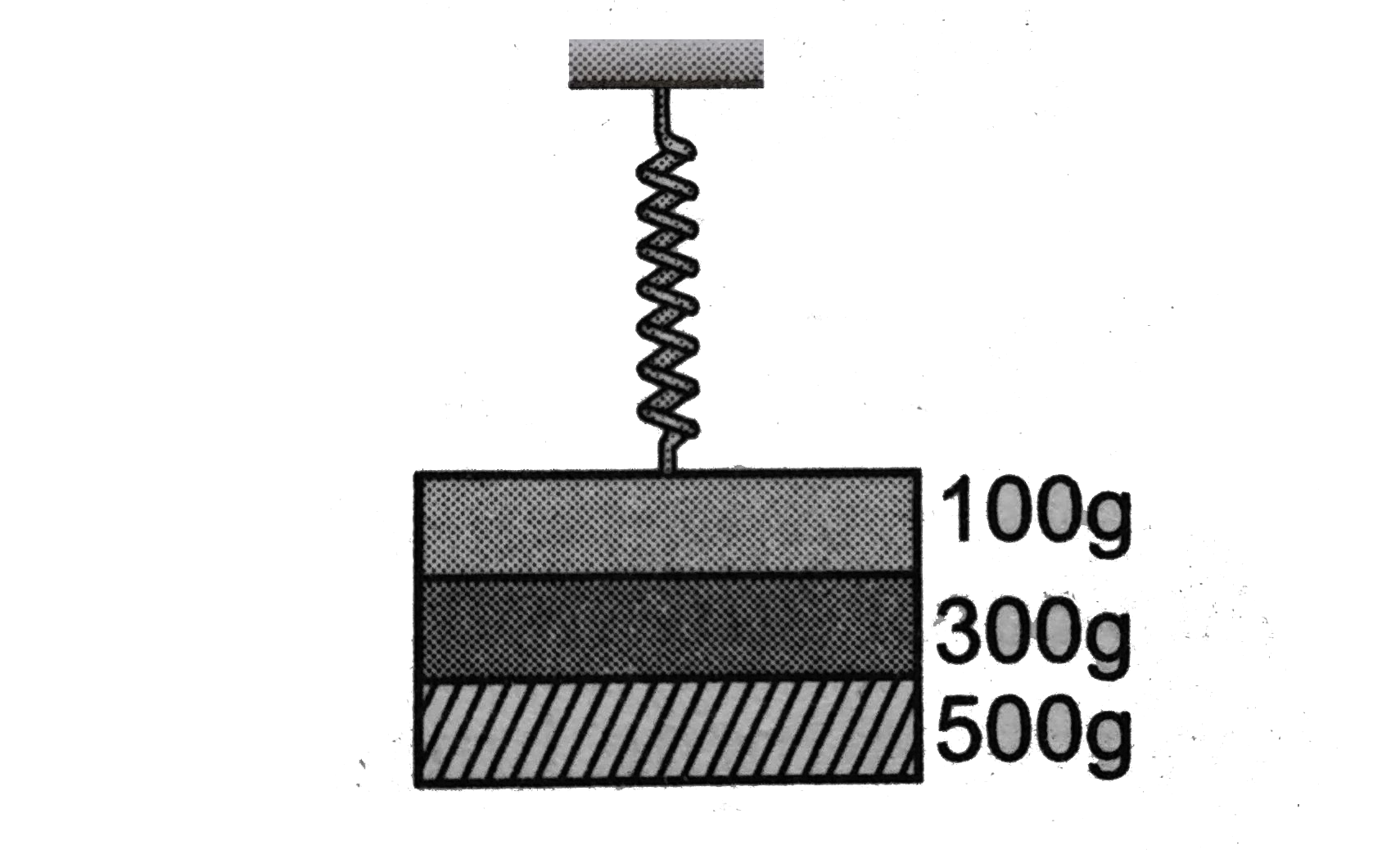
View SolutionThree masses of 500g, 300g and 100g are suspended at the end of a spring as shown and are in equilibrium. When the 500g mass is removed suddenly, the system oscillates with a period of 2s. When the 300g mass is also removed, it will oscillate with period T. Find the value of T.
View SolutionThe coordinates of the centre of mass of a system of three particles of mass 1g,2g and 3g are (2,2,2). Where should a fourth particle of mass 4 g be positioned so that the centre of mass of the four particle system is at the origin of the three-dimensional coordinate system ?
View SolutionFind the ratio of the number of atoms present in 16 g of O_2 and 32 g of O_3.
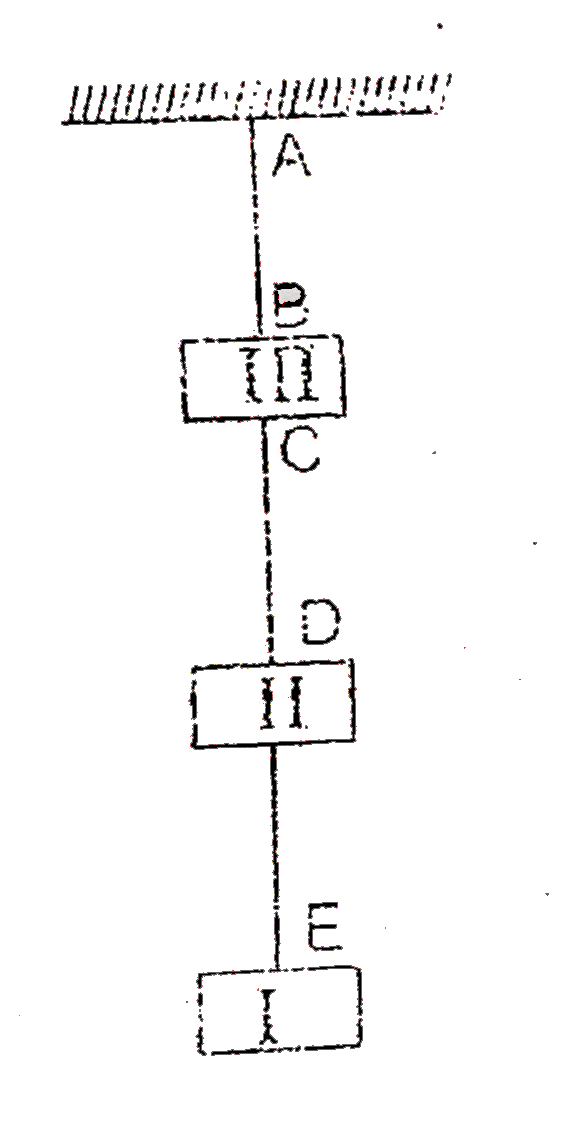
View SolutionThree blocks I,II, & III having mass of 1.6kg, 1.6kg and 3.2kg repectively are connected as shown in the figure. The linear mass density of the wire AB,CD and DE are 10g/m,8g/m and 10g/m respectively. The speed of a transverse wave pulse produced in AB,CD and DE are : (g=10m/sec2)
View SolutionActive mass of 5.6 g CaO(s) is
View SolutionFind the value of 5√32.16 correct to 4 decimals places
View Solution
