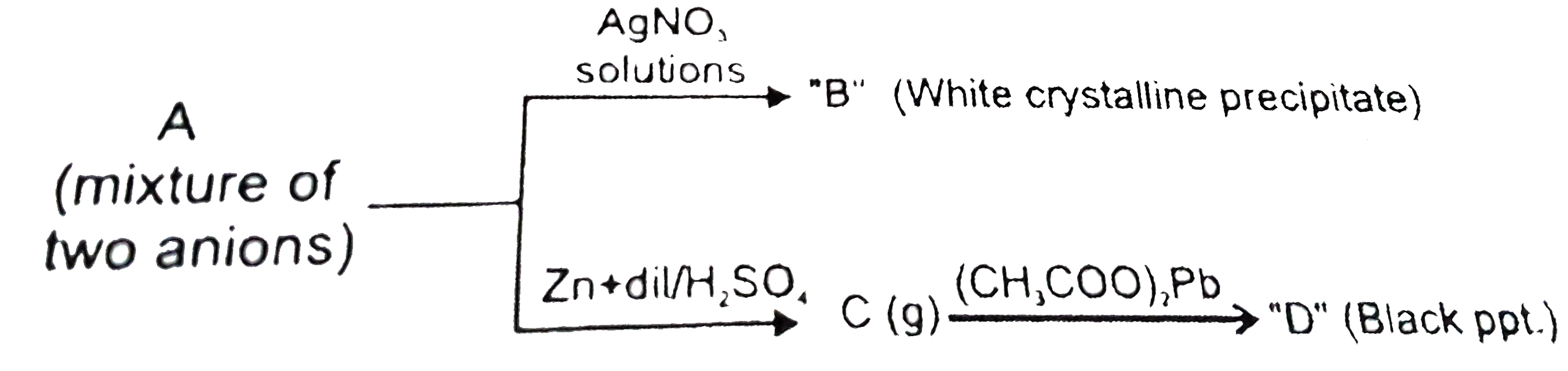STATEMENT-1 A dimensionless quantity may have a unit
STATEMENT-2 A constant may not be unitless.
Statement-1 is True , Statement-2 is True ,Statement-2 is a correct explanation for Statement-1
Statement-1 is True , Statement-2 is True ,Statement-2 is NOT a correct explanation for Statement-1
Statement-1 is True , Statement-2 is False
Statement-1 is False, Statement-2 is True
The correct Answer is:2
To analyze the statements provided, we will break down each statement and provide a clear explanation for both.
Step 1: Analyze Statement 1
- Statement 1 claims that a dimensionless quantity may have a unit.
- A dimensionless quantity is defined as a quantity that has no physical dimensions and is represented by a dimension of L0M0T0.
- An example of a dimensionless quantity is angular displacement, which can be expressed in radians.
- Radians are derived from the ratio of two lengths (arc length to radius), where both lengths are measured in meters. Hence, the units cancel out, making it dimensionless. However, it still has a unit (radian).
- Therefore, Statement 1 is True.
Step 2: Analyze Statement 2
- Statement 2 claims that a constant may not be unitless.
- A constant in physics often has units associated with it. For example, in Hooke's Law, the restoring force F is proportional to the displacement x from the mean position, represented as F=−kx.
- Here, k is the spring constant, which has units of Newtons per meter (N/m). This clearly shows that k is not unitless.
- Therefore, Statement 2 is also True.
Step 3: Determine the Relationship Between the Statements
- While both statements are true, Statement 2 does not adequately explain Statement 1.
- Statement 1 discusses the nature of dimensionless quantities, while Statement 2 discusses the nature of constants. They are related but do not directly explain each other.
- Thus, the conclusion is that both statements are true, but Statement 2 is not a correct explanation of Statement 1.
Final Conclusion:
- Statement 1: True
- Statement 2: True
- Explanation Relationship: Statement 2 does not correctly explain Statement 1.
- Statement 1 claims that a dimensionless quantity may have a unit.
- A dimensionless quantity is defined as a quantity that has no physical dimensions and is represented by a dimension of L0M0T0.
- An example of a dimensionless quantity is angular displacement, which can be expressed in radians.
- Radians are derived from the ratio of two lengths (arc length to radius), where both lengths are measured in meters. Hence, the units cancel out, making it dimensionless. However, it still has a unit (radian).
- Therefore, Statement 1 is True.
- Statement 2 claims that a constant may not be unitless.
- A constant in physics often has units associated with it. For example, in Hooke's Law, the restoring force F is proportional to the displacement x from the mean position, represented as F=−kx.
- Here, k is the spring constant, which has units of Newtons per meter (N/m). This clearly shows that k is not unitless.
- Therefore, Statement 2 is also True.
- While both statements are true, Statement 2 does not adequately explain Statement 1.
- Statement 1 discusses the nature of dimensionless quantities, while Statement 2 discusses the nature of constants. They are related but do not directly explain each other.
- Thus, the conclusion is that both statements are true, but Statement 2 is not a correct explanation of Statement 1.
- Statement 1: True
- Statement 2: True
- Explanation Relationship: Statement 2 does not correctly explain Statement 1.
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBook:AAKASH INSTITUTE ENGLISHChapter:UNITS AND MEASUREMENTSExercise:ASSIGNMENT SECTION F (Matrix-Match)
Explore 6 Videos
- UNITS AND MEASUREMENTSBook:AAKASH INSTITUTE ENGLISHChapter:UNITS AND MEASUREMENTSExercise:ASSIGNMENT SECTION G (Integer)
Explore 8 Videos
- UNITS AND MEASUREMENTSBook:AAKASH INSTITUTE ENGLISHChapter:UNITS AND MEASUREMENTSExercise:ASSIGNMENT SECTION D (Linked Comprehension)
Explore 3 Videos
- THERMODYNAMICSBook:AAKASH INSTITUTE ENGLISHChapter:THERMODYNAMICSExercise:ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
Explore 10 Videos
- WAVE OPTICSBook:AAKASH INSTITUTE ENGLISHChapter:WAVE OPTICSExercise:Assignment (Section-J (Aakash Challengers question))
Explore 1 Video
Similar Questions
Knowledge Check
Chordates may not have a
Avertebral columnBdorsal nerve cordCgill slitsDnotochord
An object may have
View SolutionA : A dimensionless quantity may have unit.
R : Two physical quantities having same dimensions, may have different units.
View SolutionSTATEMENT 1: Two quantities with different dimensions may have same unit.
STATEMENT-2 Two quantities with different units may have same dimensions
STATEMENT-3 Unitless quantities must be dimensionless too
View SolutionSTATEMENT-1 Dimensional constants are the quantities whose values are constant
STATEMENT 2 Quantities which are dimensionless are known as dimensional constants
View SolutionSTATEMENT-1: Dimensional constants are the quantities whose values are constant
STATEMENT-2: Dimensional constants are dimensionless
STATEMENT-3 Universal gravitational constant (G) is a dimensional constant
View SolutionSTATEMENT-1: Kilowatt hour is a unit of power
STATEMENT-2: Work done energy have same SI units.
STATEMENT-3: Dimensions of work is ML2T2.
View SolutionSTATEMENT-1 : A positively charged body, may have negative potential.
and
STATEMENT-2 : A positively charged body have electrons inside it.
View Solution