Which of the following represents pair of equal sets?
A={1,2,3},B={x:x∈Nandx>5}
A={B,O,W,L},B={x:x is a letter of the word ELBOW}
A={1,4,9,16},B={x:x=n2and0<n<5}
A=ϕ,B=(O,E,A)
The correct Answer is:C
To determine which pairs of sets are equal, we need to analyze each given pair of sets and check if they contain the same elements.
1. Identify the Sets:
- Set A: {1, 2, 3}
- Set B: {x | x ∈ Natural Numbers and x > 5}
2. Check Equality for Set A and Set B:
- Set A contains the elements {1, 2, 3}.
- Set B contains elements greater than 5, which are {6, 7, 8, ...}.
- Since the elements of Set A are not present in Set B, A ≠ B.
3. Next Pair of Sets:
- Set A: {b, o, w, l}
- Set B: {l, o}
4. Check Equality for Set A and Set B:
- Set A contains the elements {b, o, w, l} (4 elements).
- Set B contains the elements {l, o} (2 elements).
- Since the number of elements in both sets is different, A ≠ B.
5. Third Pair of Sets:
- Set A: {1, 4, 9, 16}
- Set B: {x | x = n², n > 0 and n < 5}
6. Check Equality for Set A and Set B:
- For n = 1, n² = 1
- For n = 2, n² = 4
- For n = 3, n² = 9
- For n = 4, n² = 16
- Thus, Set B contains the elements {1, 4, 9, 16}.
- Since both sets contain the same elements, A = B.
7. Fourth Pair of Sets:
- Set A: {5}
- Set B: {0}
8. Check Equality for Set A and Set B:
- Set A contains the element {5}.
- Set B contains the element {0}.
- Since the elements are different, A ≠ B.
Conclusion:
The only pair of equal sets is the third pair: Set A = {1, 4, 9, 16} and Set B = {x | x = n², n > 0 and n < 5}.
- Set A: {1, 2, 3}
- Set B: {x | x ∈ Natural Numbers and x > 5}
- Set A contains the elements {1, 2, 3}.
- Set B contains elements greater than 5, which are {6, 7, 8, ...}.
- Since the elements of Set A are not present in Set B, A ≠ B.
- Set A: {b, o, w, l}
- Set B: {l, o}
- Set A contains the elements {b, o, w, l} (4 elements).
- Set B contains the elements {l, o} (2 elements).
- Since the number of elements in both sets is different, A ≠ B.
- Set A: {1, 4, 9, 16}
- Set B: {x | x = n², n > 0 and n < 5}
- For n = 1, n² = 1
- For n = 2, n² = 4
- For n = 3, n² = 9
- For n = 4, n² = 16
- Thus, Set B contains the elements {1, 4, 9, 16}.
- Since both sets contain the same elements, A = B.
- Set A: {5}
- Set B: {0}
- Set A contains the element {5}.
- Set B contains the element {0}.
- Since the elements are different, A ≠ B.
The only pair of equal sets is the third pair: Set A = {1, 4, 9, 16} and Set B = {x | x = n², n > 0 and n < 5}.
Topper's Solved these Questions
- SETS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - SECTION-B(Objective Type Question(One option is correct))
13 Videos
- SETS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - SECTION-C(Objective Type Questions(More than one options are correct))
6 Videos
- SETS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - Try yourself
50 Videos
- SEQUENCES AND SERIES BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEQUENCES AND SERIES EXERCISE - Assignment (SECTION - J) Aakash Challengers
11 Videos
- STATISTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STATISTICSEXERCISE - Section-C Assertion-Reason
15 Videos
Similar Questions
Knowledge Check
Which of the following represents a pair of enantiomers?
A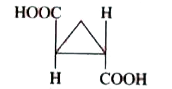 B
B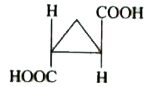 C
C D
D
Which of the following pair represent pair of diastereomers ?
AMeso tartaric acid and (l) tartaric acidB C
C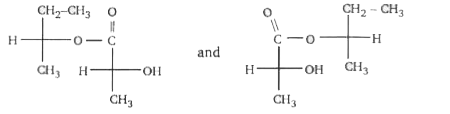 DAll of these
DAll of theseWhich of the following pairs represents anomers ?
A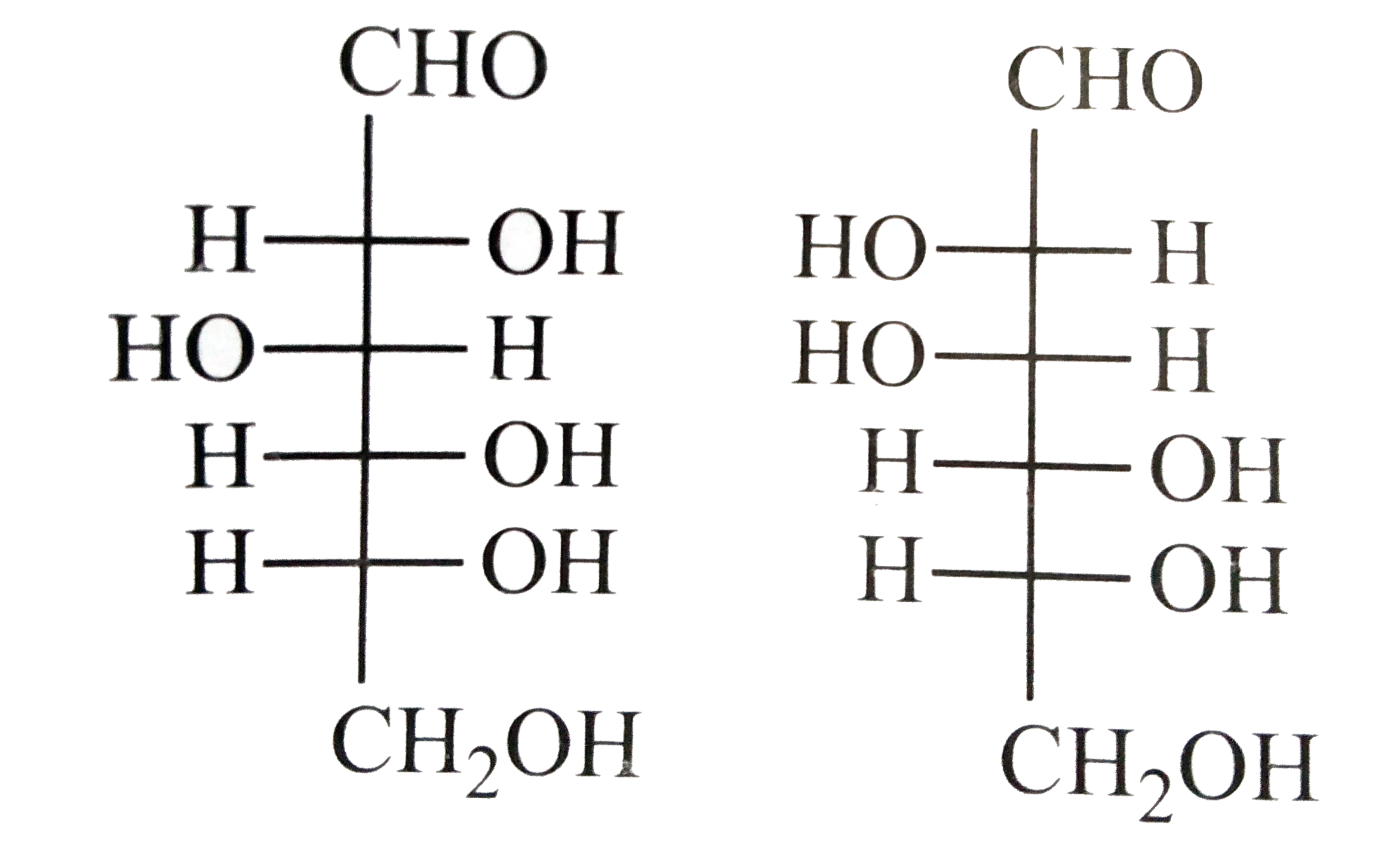 B
B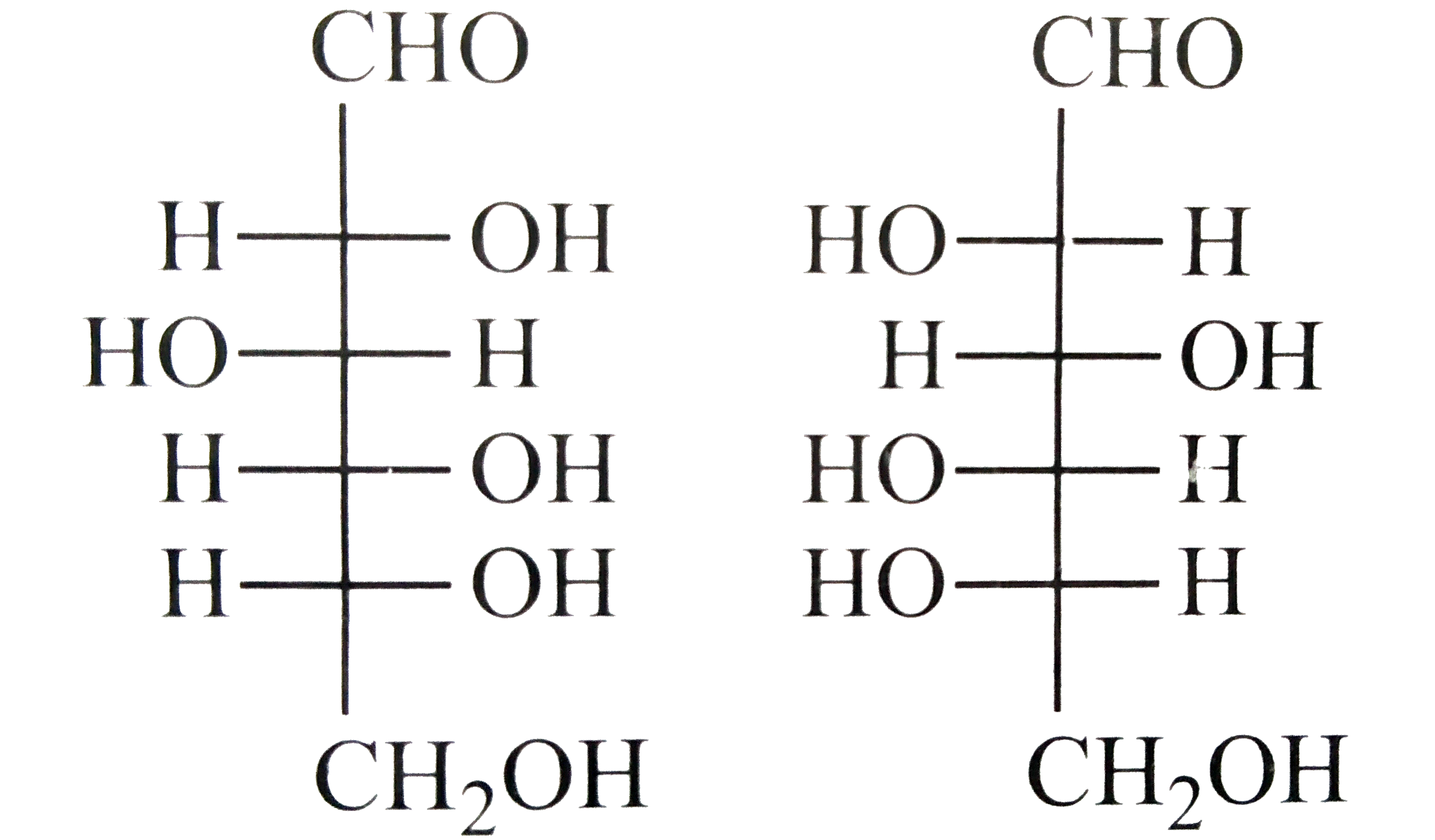 C
C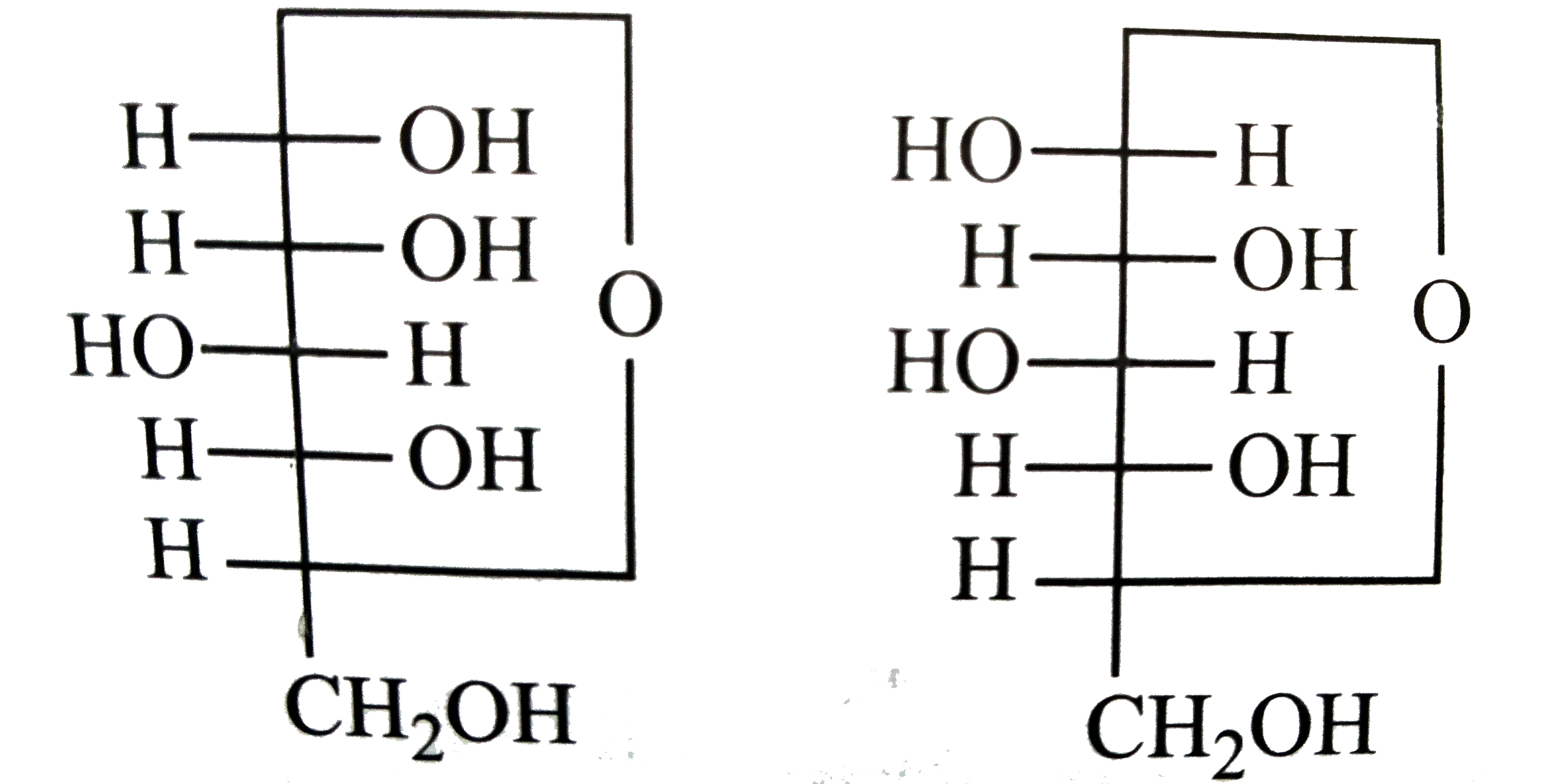 D
D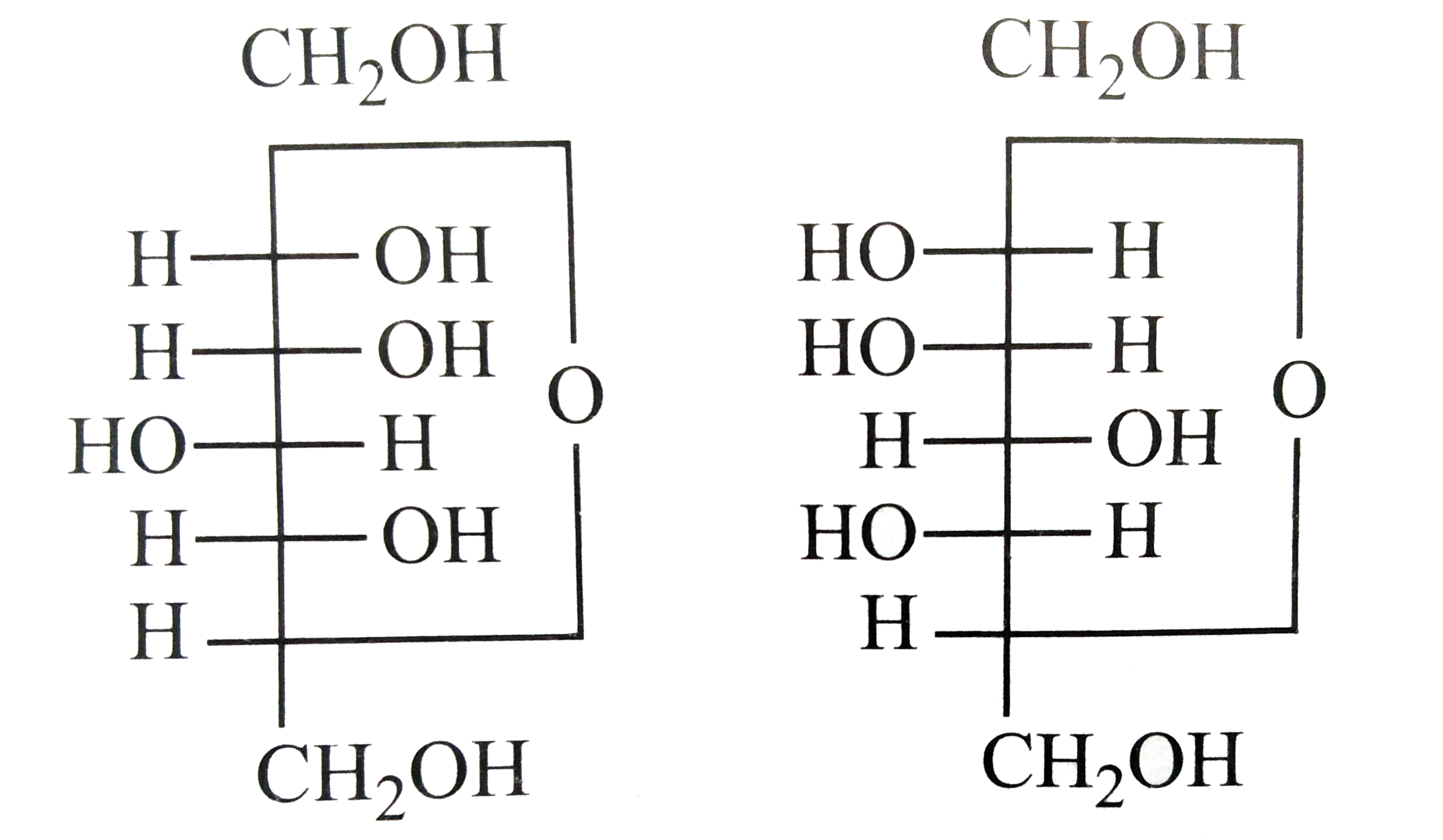
Which of the following pairs represents isobars?
View SolutionWhich of the following represent correct pair of homologous ?
View SolutionWhich of the following represents earliest set of haploid structures to appear during gametogenesis?
View SolutionWhich of the follwing represent power set of (0,3)?
View SolutionWhich of the following pairs represent of the same physical quantities?
View Solution
